Неевклидова геометрия



Неевклидова геометрия (или геометрия Лобачевского) основана на отрицании пятого постулата Евклида, утверждающего, что на плоскости через точку проходит единственная прямая, параллельная данной прямой. В отличие от классической геометрии, пространство здесь не плоское, а имеет некоторую кривизну (модели пространства — воронка или седло). Неевклидова геометрия позволяет уяснить важность математических методов для понимания фундаментальных законов природы, объектов и структур, которые не могут быть точно описаны классической евклидовой геометрией.

Ключевые слова: постулаты Лобачевского, кривизна пространства, ультрапараллельные прямые, сферический и гиперболический треугольник.

Геометрия (греч. γεωμετρία, буквально — землемерие) — раздел математики, изучающий пространственные отношения и формы и сходные с пространственными по своей структуре. Становление геометрии как математической науки связано с именами греческих ученых Фалеса (625–547 гг. до н. э.), Пифагора (580–500 гг. до н. э.), Демокрита (460–370 гг. до н. э.), Евклида (III век до н. э.) и др. Согласно классификации Ф.Клейна, в классической геометрии выделены основные разделы:

1. Евклидова геометрия.
2. Планиметрия.
3. Стереометрия.
4. Проективная геометрия. 5. Аффинная геометрия.
5. Начертательная геометрия.

Современная же геометрия содержит дополнительные разделы такие, как:

1. Многомерная геометрия.
2. Неевклидова геометрия (эллиптическая, гиперболическая, сферическая).
3. Риманова геометрия.
4. Топология.

В развитии геометрии можно выделить четыре основных периода.

Первый , период зарождения геометрии, связан с развитием науки в Египте, Вавилоне и Греции примерно до 5 в. до н. э. Геометрические сведения появились на ранних ступенях развития общества. Зачатками считают установление общих закономерностей между геометрическими величинами. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении многих поколений она складывалась в стройную систему, накапливались новые знания, выяснялись связи между фактами, формировались понятия о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл к тому, что геометрия превратилась в самостоятельную науку, появились систематические изложения с доказательствами.

С этого времени начинается второй период развития геометрии. Решающую роль в развитии геометрии сыграли «Начала» Евклида, где геометрия представлена так, как её понимают и теперь: это наука о пространственных формах и отношениях, развиваемая в логической последовательности, исходя из основных положений — аксиом и основных пространственных представлений. Это евклидова геометрия.

Третий этап связан с возрождением наук и искусств в Европе. Принципиальный шаг сделан в 1-й половине 17 в. Р. Декартом, который ввёл в геометрию метод координат. Он позволил связать геометрию с алгеброй и математическим анализом. Применение методов этих наук в геометрии породило аналитическую и дифференциальную геометрию. Геометрия перешла на качественно новую ступень.

Четвёртый период в развитии геометрии начинается с построения неевклидовой геометрии (1826 г). Ее основоположником является русский математик и деятель университетского образования и народного просвещения Николай Иванович Лобачевский. Независимо от Лобачевского ту же геометрию построил Я. Больяй (1832 г) и развивал К. Гаусс, но он не опубликовал свои результаты. Неевклидова геометрия исследует геометрические системы, отличные от классической евклидовой геометрии. Она основывается на несколько других аксиомах и принципах, что позволяет рассматривать более сложные и необычные формы пространства, решать более сложные задачи. Сейчас ведется изучение многомерной геометрии, неевклидовой, римановой геометрии и топологии.

Геометрия Лобачевского представляет собой эпоху в развитии математики. Анализируя попытки доказать пятый постулат Евклида, Лобачевский сделал вывод о его недоказуемости, что привело к возможности говорить о другой геометрии — неевклидовой, суть которой заключается в отрицании пятого постулата Евклида. Пятый постулат геометрии Лобачевского утверждает, что если на плоскости лежат прямая и точка, то через эту точку можно провести хотя бы две прямые, не пересекающиеся с первой прямой.

Свойства неевклидовых движений:

1. Суперпозиция неевклидовых движений есть снова неевклидово движение. Это вытекает из определения неевклидова движения.
2. При движении образами неевклидовых отрезков, прямых, лучей и углов являются соответственно неевклидовы отрезки, прямые, лучи и углы. Это следует из свойств инверсии и евклидовой осевой симметрии. Неевклидовы углы, преобразующиеся друг в друга неевклидовым движением, равны в смысле приведенного ранее определения, и их величины также равны.
3. Если неевклидово движение переводит неевклидов луч в себя, то либо это тождественное преобразование, либо неевклидова осевая симметрия относительно неевклидовой прямой, содержащей данный луч. Все точки прямой для данного преобразования неподвижны.

Основные отличия неевклидовой геометрии от евклидовой

*Для точки, находящейся от заданной прямой на определенном расстоянии, Лобачевский придумал формулу для угла параллельности П(a):

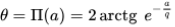
– Если прямые имеют общий перпендикуляр, то они ультрапараллельны, следовательно, бесконечно расходятся в обе стороны от него.

– В геометрии Лобачевского треугольники равны, если их углы равны. Сумма углов треугольника меньше 180 и может быть близкой к нулю.

– Линия равных расстояний от прямой называется эквидистантой.

– Предел окружностей бесконечно увеличивающегося радиуса называется предельной окружностью. Предел сфер бесконечно увеличивающегося радиуса будет называться орисферой. В геометрии Лобачевского число не определяется как отношение длины окружности к диаметру.

– Чем меньше область в пространстве (на плоскости), тем меньше геометрические соотношения в ней отличаются от соотношений евклидовой геометрии.

– В неевклидовой геометрии пространство не плоское, оно имеет некоторую кривизну (модели пространства — воронка или седло).

– Геометрия Лобачевского все еще развивается многими геометрами. В ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей.

Сферы применения неевклидовой геометрии

Неевклидова геометрия имеет прямое отношение к теории относительности Эйнштейна, особенно к общей теории относительности. В теории относительности пространство и время рассматриваются как объединенная четырехмерная структура, называемая пространство-временем. Это пространство-время описывает гравитацию как изгибание пространства-времени под действием массы и энергии. В неевклидовых пространствах с кривизной, отличной от нуля, прямые линии могут искривляться и встречаться, а сумма углов треугольника может быть отличной от 180 градусов. Аналогично, в теории относительности масса и энергия создают кривизну пространства-времени, что проявляется в изгибании света и движении объектов в гравитационных полях. Таким образом, понимание неевклидовой геометрии помогает ученым лучше описывать и предсказывать физические явления, связанные с гравитацией и структурой пространства-времени в рамках теории относительности. Взаимосвязь между неевклидовой геометрией и теорией относительности подчеркивает важность математических методов для понимания фундаментальных законов природы.

Неевклидова геометрия применяется в ядерной физике, особенно при изучении структуры атомных ядер. В ядерной физике часто используются математические модели, которые описывают взаимодействие частиц внутри атомного ядра. Одной из таких моделей является модель квантовой механики, которая включает в себя неевклидовые пространства. В неевклидовых пространствах ядерные физики могут описывать движение и взаимодействие элементарных частиц, таких как протоны и нейтроны, внутри атомного ядра. Неевклидова геометрия позволяет учитывать различные физические свойства и особенности внутриядерных процессов, такие как спин, заряд, магнитные моменты и другие. Использование неевклидовой геометрии в ядерной физике помогает ученым лучше понять структуру и свойства атомных ядер, предсказывать результаты экспериментов и разрабатывать новые теории, объясняющие сложные взаимодействия внутри атомного ядра.

Геометрия Лобачевского (гиперболическая геометрия) позволяет описывать пространство с отрицательной кривизной. Поэтому она применяется в геодезии и картографии. В контексте гиперболической геометрии можно представить Землю как поверхность с отрицательной кривизной (прямые линии на этой поверхности могут быть не параллельны и не пересекаться). С ее помощью можно изучать расстояния между точками на поверхности Земли, углы между линиями и т. д. Это позволяет глубже понять геометрические свойства Земли и провести точные расчеты. То есть гиперболическая геометрия может быть использована для определения формы Земли с учетом ее особенностей и кривизны. Это новый взгляд на изучение геометрии нашей планеты.

Коррекция картографических проекций с использованием неевклидовых принципов полезна для создания более точных и реалистичных карт Земли. Поскольку гиперболическая геометрия описывает пространство с отрицательной кривизной, она может помочь ученым учитывать особенности искривления поверхности Земли при создании карт. Использование неевклидовых принципов в коррекции картографических проекций позволяет учитывать изменения масштаба, углы и расстояния на поверхности Земли более точно, чем при использовании классических евклидовых принципов. Это особенно важно при создании карт масштаба больших регионов или при работе с данными, требующими высокой точности и точности измерений. Коррекция картографических проекций с использованием неевклидовых принципов помогает улучшить визуализацию географических данных и обеспечивает реалистичное представление формы и размеров земной поверхности. Это важно для научных исследований, где точность и достоверность картографических данных играют ключевую роль.

В трехмерных моделях компьютерной графики с использованием гиперболической геометрии можно представить объекты и структуры, которые не могут быть точно описаны классической евклидовой геометрией. Это открывает новые возможности для исследования форм, структур и связей в трехмерном пространстве, которые не могут быть полностью представлены в рамках евклидовой геометрии. Эти модели могут быть полезны для визуализации сложных геометрических объектов, а также для исследования пространственных отношений и свойств, которые проявляются только в неевклидовых пространствах. Это может быть особенно полезно в области научных исследований, компьютерной графики, дизайна и архитектуры. Использование неевклидовых принципов при создании трехмерных моделей также может способствовать развитию новых математических методов и подходов к визуализации данных, что может привести к новым открытиям и инновациям в различных областях науки и технологий.

Неевклидова геометрия в компьютерных играх и головоломкахиспользуется для создания лабиринтов, где игроки могут перемещаться по петлям и изгибам, которые не существуют в обычном евклидовом пространстве. Это делает игру более увлекательной и оригинальной.

Также неевклидовая геометрия может быть использована для создания головоломок, где игрокам нужно решать сложные задачи, связанные с пространственными переходами, оптическими иллюзиями и другими нестандартными геометрическими элементами. Это способствует развитию логического мышления, пространственного воображения и креативности, а также может быть интересным способом познакомить игроков с абстрактными математическими концепциями и разнообразить игровой опыт за счет новаторских подходов к дизайну уровней и заданий.

Применение неевклидовой геометрии в архитектуре и искусствеоткрывает уникальные возможности для создания инновационных зданий, которые отличаются от традиционных архитектурных форм. Вот варианты использования в архитектуре:

1. Необычные формы и структуры. Это может включать в себя использование гиперболических поверхностей, многогранных фигур или других нестандартных геометрических элементов.
2. Пространственные решения для создания интересных визуальных эффектов и оптических иллюзий. Это полезно при проектировании общественных зданий, музеев, выставочных площадок, где важно создать уникальное пространственное воздействие на посетителей.
3. Энергоэффективность и экологическая устойчивость. Так, использование гиперболических поверхностей может способствовать лучшей циркуляции воздуха и естественному освещению внутренних помещений.
4. Инновации в конструкциях для создания устойчивых и уникальных зданий. Например, использование нестандартных геометрических форм требует разработки специальных строительных технологий и методов.

Решение задач неевклидовой геометрии требует, как правило, затрат времени, необходимых на анализ условия, подбор нужных формул и проведение вычислений. Определять значение некоторых величин математическими методами бывает сложно. Тогда на помощь приходит информатика, точнее программирование. Автором был создан калькулятор для определения значений: кривизны сферы (1), периметра сферического треугольника (2), периметра гиперболического треугольника (3), площади сферического треугольника (4), площади гиперболического треугольника (5), объема сферического / гиперболического тетраэдра (6) по формулам:

(1)

(2)

(3)

(4)

(5)

(6)

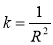
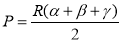
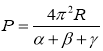
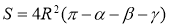
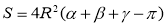
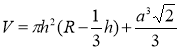
В разработанном программном коде на языке Рython данные формулы представлены в виде отдельных функций для расчета значений величин:

Диалоговое окно программы выглядит следующим образом:

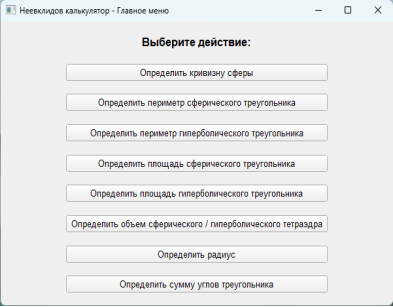
Пример. Вычисление радиуса сферического треугольника:

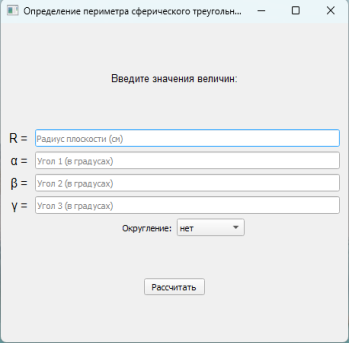
Изучить код можно по ссылке: https://github.com/nikita64347/Neevklidov-calculator. На созданном автором сайте можно получить различные сведения по теме «Геометрия Лобачевского», а также примеры решения задач, и задать вопросы.Ссылка на сайт: http://37.46.128.165/.

Многие задачи из разных областей наук решаются с помощью неевклидовой геометрии. Кажущееся, на первый взгляд, странным и непонятным искажение пространства в неевклидовой геометрии на самом деле подчиняется строгим законам, аксиомам и теоремам геометрии. Именно ее использование помогает двигать науку вперед. Она позволяет лучше понимать структуру пространства и развивать новые методы анализа и решения задач. Неевклидова геометрия представляет собой увлекательную область математики, которая имеет широкие применения в различных сферах наук: в физике, в информационных технологиях, в геодезии, в архитектуре и в других областях. Изучение этой темы может привести к новым открытиям и дальнейшему развитию науки.

Литература:

1. Бижанова С. А., Гордиенко Е. А. и др. О геометрии кривых на плоскости Н. И. Лобачевского — Лобачевский и XXI век: материалы V научно-образовательной студенческой конференции, ко Дню рождения Н. И. Лобачевского /под ред. Л. Р. Шакировой. — Казань: Изд. Казан. ун-т, 2018.
2. Козлов, Н. В. Использование неевклидовой геометрии в геймдизайне. — Сборник статей по материалам 59-й научной конференции аспирантов, магистрантов и студентов БГУИР, Минск, 2023.
3. Ктитров С. В., Рысляев Д. А. Статья «Сравнительный графический анализ искажений некоторых картографических проекций» — журнал «Научная визуализация», 2022.
4. Курочкин Ю. Специальная теория относительности и геометрия Лобачевского — Наука и инновации: научно-практический журнал / гл. ред. Ж. В. Комарова; учредитель Национальная академия наук Беларуси (Минск). — 2016.
5. Перелешин С. А., Чурина Д. С., Шумкина Т. Ф. Виды геометрий и их особенности. — Сборник статей по материалам VIII научно-практической конференции молодых ученых. Кузбасский государственный технический университет имени Т. Ф. Горбачева, 2016.
6. Хриплович И. Б. Общая теория относительности. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.