1. Введение
Если взять окружность любого радиуса и посчитать отношение длины этой окружности к её диаметру мы получим знаменитую математическую простоянную π = 3,1415926535897932384626433832795…
Нужно заметить, что данное определение действительно только для евклидовой геометрии. В других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Минковского—Банаха
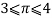
Существует множество способов, алгоритмов и формул для вычисления численного значения числа π. Например, формулы типа Мэчина:
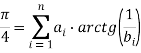
названные в честь Джона Мэчина, который в 1706 году нашёл эффективную формулу для вычисления числа π [2]:
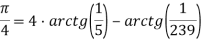
Данная формула позволяет вычислить число π используя разложение функции
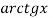
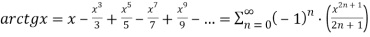
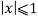
В данной работе рассчитаем отношение длины кривой к её диаметру для лемнискаты Бернулли. Полученное значение отношения называется лемнискатной постоянной ω.
Для вычисления данной постоянной ω выведем и будем использовать формулу разложение функции
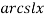
2. Лемниската Бернулли.
Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами [4].
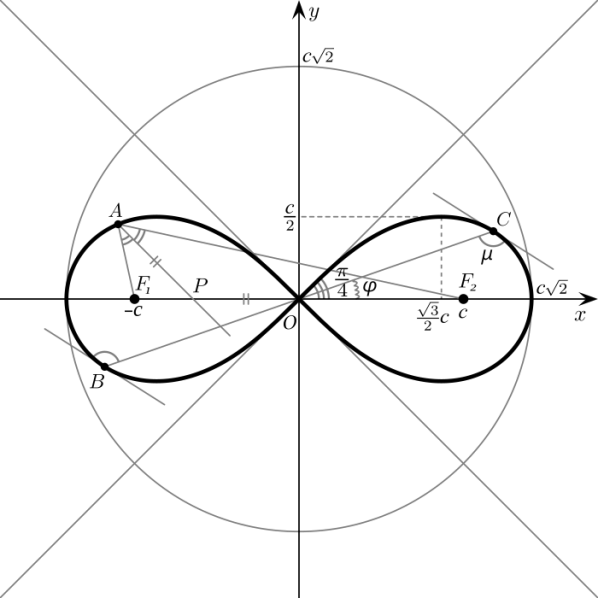
Рис.1 Лемниската Бернулли и два её фокуса F 1 и F 2
Уравнение лемнискаты:
в прямоугольных координатах:
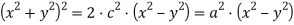
в полярных координатах:
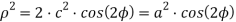
Из курса высшей математики известно, что длина всей лемнискаты выражается эллиптическим интегралом I рода [4]:
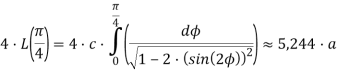

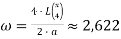
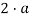
Диаметром фигуры называется максимальное расстояние между точками этой фигуры, или точная верхняя грань всевозможных расстояний, если максимальное не существует [5].
2.1. Лемнискатный синус sl x и лемнискатный арксинус arcsl x.
Рассмотрим единичную лемнискату, заданную уравнением:
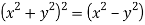
Аналогично тригонометрическиим функциям sin(x) и cos(x) определяются лемнискатный синус sl(x) и лемнискатный косинус cl(x) [6].
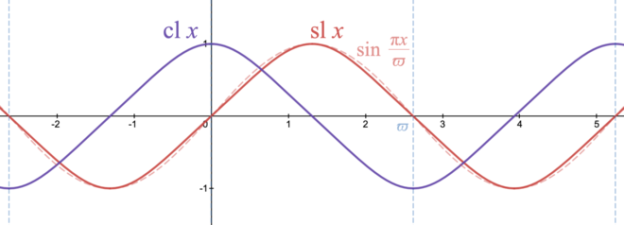
Рис. 2. Лемнискатный синус и лемнискатный косинус по сравнению с тригонометрическим синусом y = sin(πx/ω)
Формулы сложения для лемнискатного синуса выглядят следующим образом [6]:
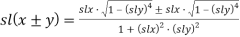
В частности
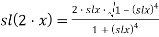
Также аналогично тригонометрическим функциям arcsin(x) и arccos(x) вводятся обратные функции к лемнискатному синусу sl(x) и лемнискатному косинусу cl(x) — лемнискатный арксинус arcsl(x) и лемнискатный арккосинус arccl(x).
По аналогии с тем, что
![[7]:](https://moluch.ru/young/blmcbn/4584/4584.019.png)
![[7]:](https://moluch.ru/young/blmcbn/4584/4584.020.png)
Геометрическая интерпретация лемнискатного арксинуса и лемнискатного арккосинуса показана на Рис. 3 [7]:
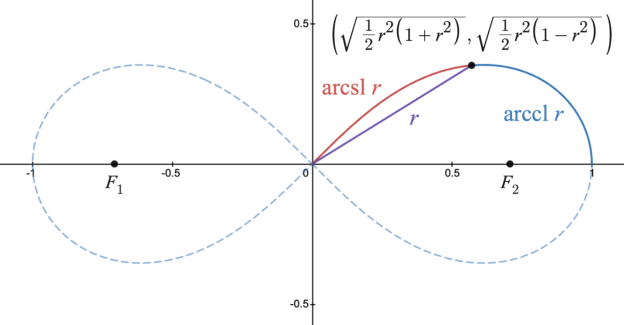
Рис. 3. Лемнискатный арксинус и арккосинус связывают длину дуги лемнискаты с расстоянием от начала координат до точки на кривой
2.2 Вывод формулы разложения лемнискатного арксинуса в ряд
Так как лемнискатный арксинус по определению равен длине дуги лемнискаты, получаем [7]:
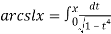
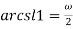
Выведем формулу разложения лемнискатного синуса в ряд.
Для этого воспользуемся формулой бинома Ньютона [2]:
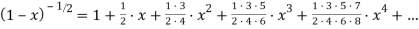
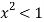
Подставим данную формулу в выражение лемнискатного арксинуса и так как ряд бинома Ньютона сходится, выполним его почленное интегрирование:
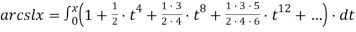
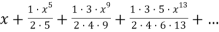
Окончательно имеем при
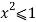
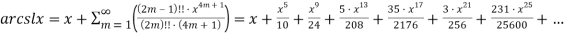
Из формулы (3) при
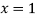
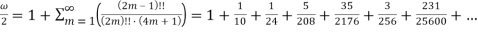
2.3 Вывод «вспомогательных» формул
1) Используя формулу (1), получим:
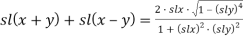
2) Из формулы (1) следует:
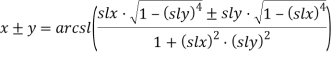
Обозначим:
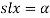
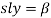
Тогда
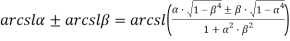
Или
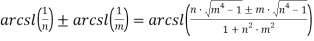
В частности
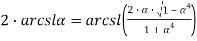
Или
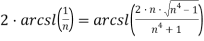
3) Вывод формулы для
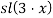
Согласно формуле (5) рассмотрим
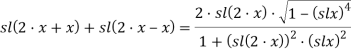
подставляя формулу (2), получим:
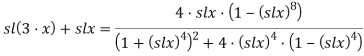
и окончательно:
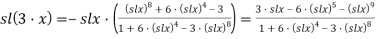
4) Вывод формулы для
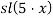
Согласно формуле (5) рассмотрим
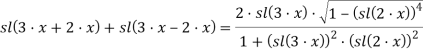
подставляя формулы (2) и (10) и в результате несложных, но громоздких вычислений, получим:
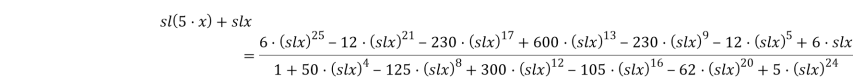
и окончательно:
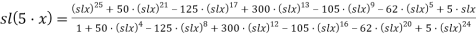
2.4 Вывод формул для вычисления лемнискатной постоянной.
Пример № 1
Решить уравнение
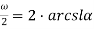
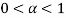
Решение.
Имеем
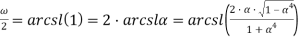
Приравнивая выражения, получим:
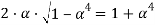
После возведения в квадрат и преобразования получим уравнение:
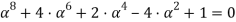
Или:
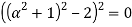
Решая данное уравнение, находим действительные корни:
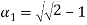
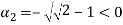
Окончательно имеем:
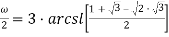
Замечание.
* Тригонометрический аналог уравнения (12):
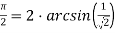
Пример № 2
Решить уравнение
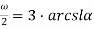
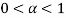
Решение.
Используя формулу (10) или результаты, указанные в [8], получаем:
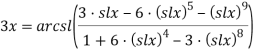
Проводя замену
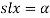
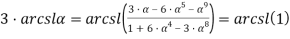
На основании вышеуказанного
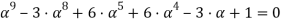
Разложим данный многочлен на множители:
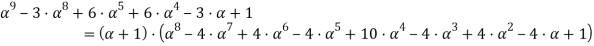
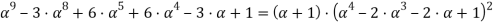
Найдем корни уравнения:
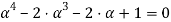
Для решения уравнения (13) воспользуемся методом Феррари [9].
Резольвента основного уравнения:
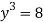
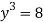
Тогда корни уравнения (13) находятся как корни уравнений:
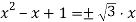
Уравнение
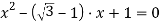
Решая уравнение
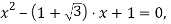
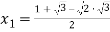
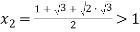
Окончательно:
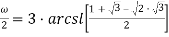
Замечание.
* Тригонометрический аналог уравнения (14):
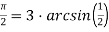
Пример № 3
Решить уравнение
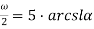
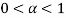
Решение.
Аналогично предыдущим примерам, используя формулу (11), получаем многочлен:
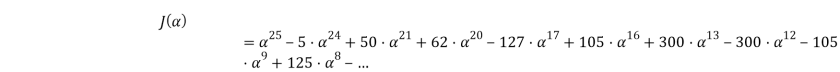
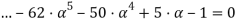
Разлагаем его на множители:
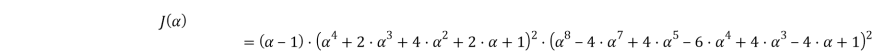
Найдем корни уравнения:
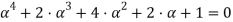
Для решения уравнения (15) воспользуемся методом Феррари [9].
Резольвента данного уравнения:
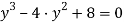
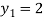
Тогда корни уравнения (15) находятся как корни уравнений:
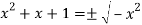
А как нетрудно видеть, данные уравнения не имеют решений в действительных числах.
Найдем корни уравнения:
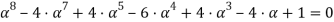
Используя «Метод неопределенных коэффициентов» [10] находим, что
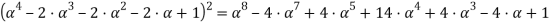
Тогда уравнение (16) можно записать в виде:
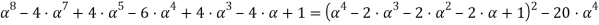
И окончательно разложение многочлена
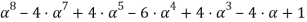
на множители:
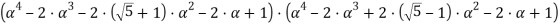
Уравнение
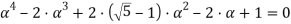
Найдем корни уравнения:
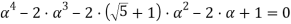
Для решения уравнения (17) воспользуемся методом Феррари [9].
Резольвента данного уравнения:
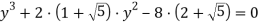
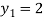
Тогда корни уравнения (17) находятся как корни уравнений:
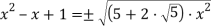
Уравнение
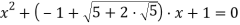
Решая уравнение
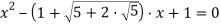
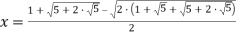
Окончательно:
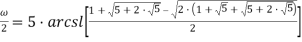
Замечания.
* Тригонометрический аналог уравнения (18):
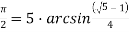
** Карл Гаусс получил для уравнения (18) более «красивое» выражение [11]:
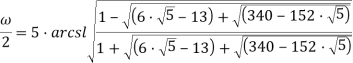
Пример № 4
Решить уравнение:
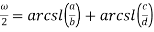
при условии:
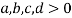
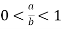
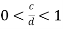
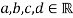
Решение.
Применяя формулу (5) к уравнению
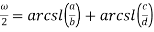
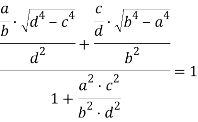
Или
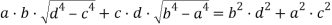
Положим
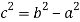
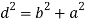
Действительно (20) являются решением уравнения (19):
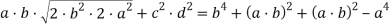
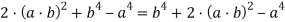
Тогда
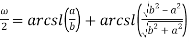
Положив
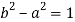
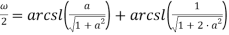
Подставляя различные значения
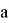
При
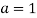
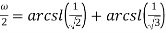
При
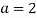
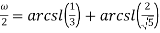
При
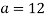
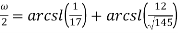
При
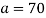
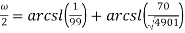
Пример № 5.
Вывести формулу:
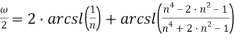
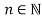
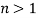
Решение.
Для этого положим в формуле (21):
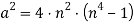
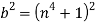
И воспользуемся формулой (9).
Получим:
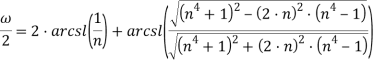
Или после преобразования:
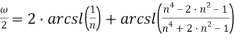
Подставляя
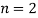
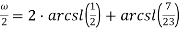
Подставляя
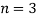
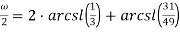
Подставляя
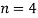
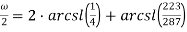
Пример № 6
Вывести формулу:
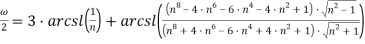
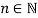
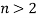
Решение.
Вычисляя
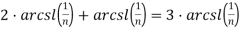
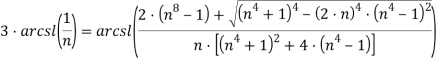
Или после преобразований:
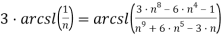
Так же для вывода формулы (29) можно воспользоваться формулой (10):
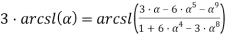
И после замены
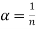
Используя формулу (21), положим:
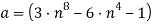
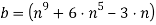
Тогда
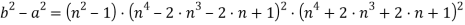
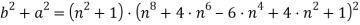
И окончательно:
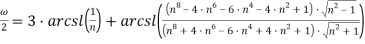
Подставляя
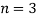
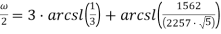
Подставляя
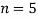
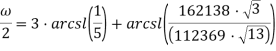
Подставляя
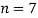
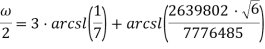
3. Вычисление лемнискатной константы ω.
Рассмотрим следующие формулы для вычисления ω:
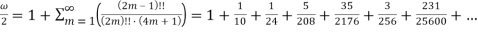
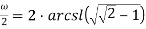
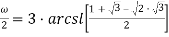
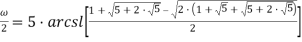
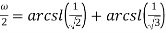
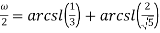
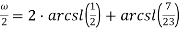
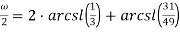
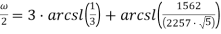
Представим данные формулы в виде
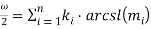
Тогда по аналогии с [12] для каждой формулы введем меру :
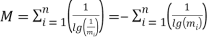
которая характеризует эффективность данной формулы. И чем мера меньше, тем формула для вычисления лемнискатной постоянной эффективней.
Для вычисления лемнискатной постоянной воспользуемся данными формулами и разложением функции
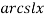
На основании полученных данных составим таблицу:
|
Номер формулы |
Мера |
Значение ω |
|
4 |
- |
2 ,44143743142604 |
|
24 |
22,734 |
2,62 185425265251 |
|
23 |
10,836 |
2,62205755 687758 |
|
27 |
7,125 |
2,6220575542 2176 |
|
26 |
5,258 |
2,6220575542921 1 |
|
12 |
5,225 |
2,622057554 00457 |
|
31 |
4,059 |
2,62205755429212 |
|
14 |
2,769 |
2,62205755429212 |
|
18 |
1,720 |
2,62205755429212 |
Выделены «верные» цифры лемнискатной постоянной.
Таким образом мною были найдены новые формулы для вычисления лемнискатной постоянной и получено её значение ω = 2,62205755429212.
На 01.07.2024 мировой рекорд в определении значения лемнискатной постоянной принадлежит Seungmin Kim и составляет 1200000000100 знаков после запятой. Установлен 17 июля 2022 года [13].
Литература:
- Жуков А. В. О числе π. — М.: МЦНМО, 2002.
- https://en.wikipedia.org/wiki/Machin-like_formula
- Двайт Г. Б. Таблицы интегралов и другие математические формулы. — М.: Наука, 1977.
- https://ru.wikipedia.org/wiki/Лемниската_Бернулли
- https://ru.wikipedia.org/wiki/Диаметр
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli
- Euler, Leonard (1761) «Observationes de comparatione arcuum curvarum irrectificibilium».
- https://ru.wikipedia.org/wiki/Метод_Феррари
- https://ru.wikipedia.org/wiki/Метод_неопределенных_коэффициентов
- Todd, John (1974) «The Lemniscate constant».
- Lehmer, D.H. (1938) «On arccotangent relations for π».
- http://www.numberworld.org/y-cruncher/







