В данной статье автор рассматривает некоторые алгоритмы решения комбинаторных задач, основанных на идее применения раскраски в несколько цветов, а также их применение для решения олимпиадных задач по математике.
Многие школьники в настоящее время участвуют в различных олимпиадах по математике — в основном для дальнейшего поступления в престижнейшие ВУЗы и получение повышенной стипендии. И для получения всех этих благ нужно достойно решать задачи, которые весьма непростые. Для правильного решения задач требуются хорошие знания в геометрии — как и планиметрии, так и стереометрии, в алгебре, в неравенствах и многих других областях математики. Одни из самых интересных, и при этом сложных задач обычно являются задачи по комбинаторике, которые могут иметь несколько способов решения. Иногда для того, чтобы решить задачу по комбинаторике, нужно применить несколько различных приёмов. Одним из методов решения задач по комбинаторике является применение раскраски. Рассмотрим этот метод и сделаем вывод — когда, как и почему его стоит применять в различных задачах
Польза раскрасок
Почему же именно раскраски? С помощью них можно как-то переиначить задачу на более простой язык — а это уже шаг в сторону упрощения решения задачи. Например, у нас есть доска 8 * 8 (рис. 1), то почему бы не раскрасить её в шахматную раскраску (рис. 2), и иногда этот шаг может очень сильно помочь в продвижении решения.

Рис. 1
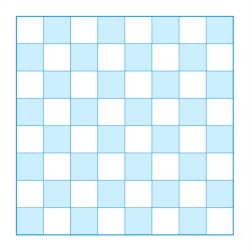
Рис. 2
Например, если в задаче сказано, что конь стартует с определённой клетки, и должен остановиться в определённой клетке за определённое количество ходов, то такая раскраска даёт понять, что на каждом ходе конь оказывается на другой по цвету клетке, что может достаточно серьёзно продвинуть решение.
Ещё раскраски могут помочь решить задачу на принцип Дирихле, когда, раскрашивая в определённые цвета, можно понять, что каких-то элементов одного цвета будет не меньше или не больше определённого значения, тем самым давая оценку для задачи вида «Оценка + Пример»
Примеры использования
Рассмотрим задачу:
На доску 8 × 8 поставили четырёх королей, не бьющих друг друга. Какое наибольшее количество королей можно гарантированно добавить на доску так, чтобы ни один король не бил другого?
Уже при прочтении можно понять, что явно стоит доску раскрасить. При этом, одной лишь раскраской эту задачу не решить.
Поэтому прилагается решение задачи (рис. 3)
Ответ: Семь.
Решение. Пример, когда нельзя добавить больше семи королей, приведён на рисунке справа. Четыре поставленных короля бьют участок 6 × 6. Оставшаяся часть разделена на семь квадратов 2 × 2, в каждый из которых можно поставить не более одного короля.
Теперь докажем, что семь всегда можно добавить. Четыре поставленных короля побьют максимум 4·9 = 36 клеток, то есть хотя бы 64 − 36 = 28 останутся не побитыми. Рассмотрим раскраску доски в четыре цвета. Заметим, что их этих 28 клеток останется хотя бы семь одного цвета. На них и поставим королей — они не будут бить друг друга.
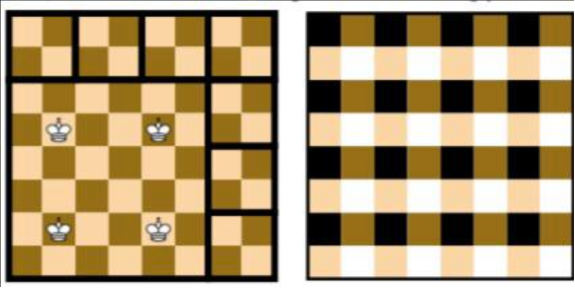
Рис. 3
Также метод использования раскрасок популярен не только в шахматных задачах. Рассмотрим задачу с муниципального этапа Всероссийской олимпиады школьников по математике в Калининграде в 2021 году под номером 8.4:
«Прямоугольник вымощен плитками размерами 1 × 4 и 2 × 2. Плитки с прямоугольника сняли и одну плитку размером 2 × 2 заменили на плитку размером 1 × 4. Докажите, что теперь новым набором плиток прямоугольник вымостить не удастся»
Давайте рассмотрим раскраску в 4 цвета (рис. 4), такую, что каждая плитка 2 × 2 содержит ровно одну клетку цвета 1, а каждая плитка 1 × 4 — ни одной или две клетки цвета 1. Следовательно, четность числа плиток 2 × 2 должна совпадать с четностью числа клеток цвета 1, что и доказывает утверждение задачи
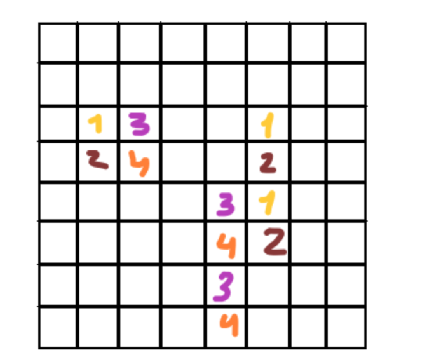
Рис. 4
Итоги
Из вышеприведённых задач можно сделать вывод, что умение решать комбинаторные задачи очень важно, ведь возможно именно они решат судьбу призёрства или прохода на следующий этап олимпиады. И поскольку задачи на комбинаторику могут в себе содержать несколько идей, то нужно понимать, что раскраски очень важны для решения таких задач.
Также идея раскраски может оказать помощь в понимании задачи, что тоже очень важно, ведь если участнику олимпиады непонятно условие задачи, то как он может её решить?
Из решений приведённых задач можно сделать вывод, что если в задаче спрашивается о шахматах (например, о передвижении коня, ладьи и т.п и т. д.), то явно стоит доску, на которой происходит действие, раскрасить в 2 цвета в шахматном порядке. Также, если нас просят что-то вырезать из какой, то большой фигуры, а потом обратно всё вернуть, то тут также стоит раскрасить изначальную фигуру в несколько цветов.










