О связи высоты и биссектрисы, проведенных из одной вершины треугольника



В данной статье рассматривается доказательство одной теоремы разными способами. Отыскание различных способов доказательства теорем — важнейшее средство развития творческого мышления учащихся, способствует более глубокому и прочному пониманию и запоминанию материала.

Ключевые слова: треугольник, высота, биссектриса, угол, косинус полуразности двух углов.

Где материя, там геометрия.

Иоганн Кеплер

Геометрия — удивительная наука, которая возникла из нужд практики. Большое число правил для решения практически важных задач можно найти уже в древнегреческих папирусах и древневавилонских клинописных текстах. Древние египтяне умели вычислять площади прямоугольника, треугольника и трапеции. Египтяне узнали, что треугольник, стороны которого пропорциональны числам 5, 4 и 3, имеет прямой угол. По-видимому, верёвочный треугольник с таким отношением сторон служил для разбивки прямых улов на местности при делении полей. Но всё это были практически найденные рецепты, иногда точные, а иногда лишь приближенные. Сами египтяне и вавилоняне такого различия, вероятно, не делали. Не было ни точных определений, ни отчётливых доказательств. Практическая деятельность человека служила основой длительного процесса выработки отвлечённых понятий, открытия простейших геометрических зависимостей и соотношений. Со времён, когда накопилось большое количество геометрических фактов, у людей появилась потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Геометрия стала наукой лишь после появления в ней теорем и доказательств. К числу основных геометрических фактов следует отнести и теорему «О связи биссектрисы и высоты в треугольнике».

Из различных источников Интернета известна теорема:

«В произвольном треугольнике отношение высоты к биссектрисе, проведенных с одного угла, равно косинусу полуразности двух других углов» (рис.1). Эта теорема выражается следующей формулой: .

Доказательство. В произвольном треугольнике АВС со сторонами ВC=a, АC=b, АВ=с из вершины угла А проведём высоту AD=h _a и биссектрису AK=l _a . Угол, образованный высотой и биссектрисой обозначим  DАK=ɤ .

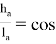
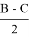
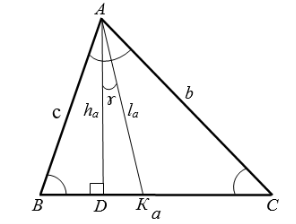
Рис. 1

Из прямоугольного треугольника ADK , находим:

, (1)

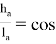
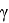
Формула угла между высотой и биссектрисой произвольного треугольника:

, (2)

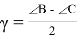
Для доказательства этой формулы будем использовать свойство углов треугольника, согласно которому их сумма равна

180º:  A=180º — B — C , (3)

Рассмотрим BAК. Используя выражение (3), с учётом, что AК — биссектриса, будем иметь:

BAК= A или BAК= ( 180º — B — C ), (4)

Рассмотрим BAD. Так как по условию AD — высота, то по свойству углов прямоугольного треугольника будем иметь:

BAD=90º – B , (5)

По построению BAК = BAD+ , отсюда

BAК — BAD , (6).

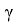
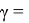
Используя выражения (4), (5) и (6), получим:

или , (7)

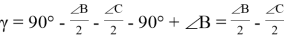
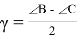
Таким образом, формула угла между высотой и биссектрисой произвольного треугольника выведена. Используя выражения (1) и (7), будем иметь: , что и требовалось доказать.

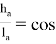
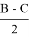
Эта теорема интересна тем, что существует ещё несколько способов её доказательства (авторские).

Известно, что в треугольнике АВС высота, проведённая из вершины угла А , выражается следующей формулой:

, (8)

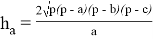
где a, b, c — стороны треугольника; p — полупериметр. Известно, что в треугольнике АВС биссектриса, проведённая из вершины угла А , выражается следующей формулой:

, (9)

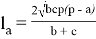
Разделив выражение (8) на (9), получим:

, отсюда

, (10)

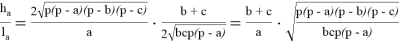
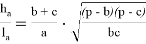
Используя выражение (10), с учётом, что

, будем иметь: , (11)

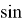
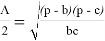
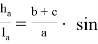
Используя выражение (11), с учётом, что

(формула Мольвейде), получим: , (12)

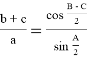
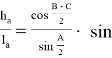
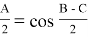
что и требовалось доказать.

Площадь треугольника АВС можно выразить следующими формулами:

, (13) и , (14)

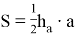
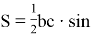
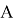
Приравняв выражения (13) и (14), найдём:

, (15)

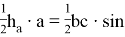
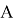
Известно, что в треугольнике АВС биссектриса, проведённая из вершины угла А , выражается следующей формулой:

, (16)

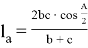
Разделив выражение (15) на (16), получим:

= , (17)

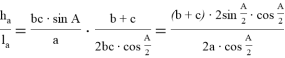
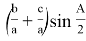
Из треугольника АВС по теореме синусов имеем:

, (18) и , (19)

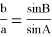
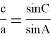
Используя выражения (17), (18) и (19), будем иметь:

,

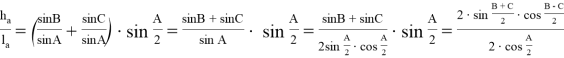
отсюда

, (20)

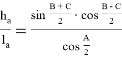
Учитывая выражение (20) и что

,

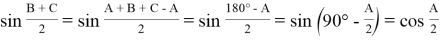
получим: , отсюда , что и требовалось доказать.

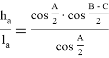
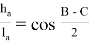
Из прямоугольного треугольника ADК найдём:

, (21)

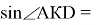
Рассмотрим СAК . Так как AК в треугольнике АВС является биссектрисой, следовательно

СAК= A , (22)

Рассмотрим треугольник AКС . Используя свойства углов треугольника, согласно которому их сумма равна 180º, будем иметь:

AКС=180º +С) , (23)

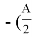
Из условия, что сумма двух смежных углов равна180º, будем иметь:

AКD=180º AКС , (24)

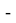
Используя выражения (23) и (24), получим:

AКD=180º 180º 180º = = , то есть AКD= , (25)

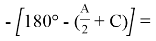
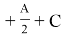
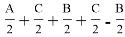
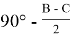
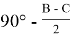
Используя выражения (21) и (25), получим:

,

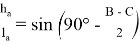
Отсюда

, что и требовалось доказать.

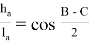
Задача 1. В треугольнике AВC из вершины угла A проведены высота AD= и биссектриса AK= . Найти отношение высоты к биссектрисе, если B=75º,С=45º (рис.1).

Задача 2. В треугольнике AВC из вершины угла A проведены высота AD= и биссектриса AK= . Найти B , если известно, что С=45º и отношение высоты к биссектрисе равно 0,966.

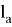
В представленной работе рассмотрены различные способы доказательства одной и той же теоремы. Учитель, приучая учащихся к самостоятельному поиску доказательства, поощряя их работу в этом направлении (даже, если найденное доказательство сложнее известного), может добиться более прочных и глубоких знаний, способствовать повышению интереса к предмету. Благодаря такой работе над доказательством теорем разными способами формируется логическое мышление. Подробный разбор способов доказательства теоремы разными способами является хорошим подспорьем для того, чтобы освежить в памяти пройденный материал.

Таким образом, отыскание различных способов доказательства одной и той же теоремы — важнейшее средство развития творческого мышления учащихся.

Литература:

1. Василевский А. Е. Методы решения математических задач. Минск, 1969.
2. Литвиненко В. Н. Практикум по решению задач школьной математики (Геометрия).
3. Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
4. Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.