В рамках данной статьи будут представлены новые информационные технологии WolframAlpha в построении и исследовании эконометрической модели фондового рынка, связывающей две случайные переменные: доходность некоторого финансового актива и доходность рынка в целом. Проведенный анализ позволил выявить содержательный смысл параметров модели Ульяма Шарпа.

Ключевые слова: WolframAlpha, моделирование, модель, эконометрика, зависимость, математическая подготовка, бакалавр экономики, модель Шарпа

В центре внимания данной статьи специфические особенности построения и исследования широко известной модели финансового анализа, автором которой является популярный американский экономист, лауреат Нобелевской премии Уильям Шарп. Учитывая современные социально-экономические условия, характеризующиеся актуализацией рисков различной природы [7] модель Шарпа целесообразно воспринимать как достаточно востребованный и эффективный исследовательский инструмент. Отметим, что инструментальная реализация модели Шарпа — одной из моделей фондового рынка — позволяет инвестиционным домам и фондам, а также международным банкам и частным инвесторам количественно оценивать риски вложений в те или иные финансовые инструменты.

В таблице 1 представлены данные торгов по четырем финансовым инструментам «Аэрофлот», «ВТБ», «Магнит», «Газпром», а также значения фондового индекса «RTS» — основного индикатора фондового рынка России согласно данным сайта http://www.finanz.ru/. Для построения и последующего исследования модели Шарпа нами будет использован значительно небольшой отрезок времени — с 24.03.2017 по 06.04.2017 (это связано с ограничением на длину запроса в базовой версии используемого инструментального средства WolframAlpha [3]).

Таблица 1

Таблица 2 содержат результаты вычисления доходностей четырех финансовых инструментов, перечисленных ранее, и ежедневные изменения значений фондового индекса «RTS». Отметим, что положительное значение означает увеличение значений параметров в результате торгов, отрицательные значения свидетельствуют о уменьшении, нулевые значения — об отсутствии изменений по результатам торгов.

Таблица 2

Сущность модели Шарпа [8] заключается в идеи дополнения и упрощения уже используемых методов построения инвестиционных портфелей, существенном понижении трудоемкости процесса финансового анализа. Основу модели Шарпа составляет эконометрический анализ [6] финансового рынка, другими словами — регрессионный анализ данных котировок. Следуя теоретическим построениям, выполненным Уильямом Шарпом, отметим, что бета-коэффициент определяет характер зависимости конкретного финансового актива от динамики рынка в целом (индекса). С другой стороны, альфа-коэффициент характеризует доходность финансового актива вне зависимости от конъюнктуры рынка. По предположению бета-коэффициент достаточно статичен от одного периода анализа к другому, и поэтому для его оценки традиционно применяют методы линейной регрессии. Содержательный смысл коэффициента альфа-коэффициента заключается в оценке переоцененности (в случае положительного значения) и недооцененности финансового актива относительно рынка в целом (в случае отрицательного значения).

Для построения линейной регрессии в новой базе знаний и наборе вычислительных алгоритмов нами будет использован запрос вида «Linear fit (x, y)», реализующий построение линейной модели по множеству упорядоченных пар значений независимого и зависимого параметра. Отметим, что в контексте модели Шарпа независимым параметром является доходность рынка в целом, а зависимым параметром принято считать доходность конкретного финансового инструмента.

Отметим, что WolframAlpha позволяет не только получать результат, освобождая от рутинных вычислений, но и предоставляет исследователю уникальные возможности по визуализации [1] социально-экономических ситуаций. Интеграция информационных и педагогических технологий в системе математической подготовки бакалавра экономики [2] позволяет по-новому подойти к организации учебно-познавательной деятельности студентов экономического бакалавриата, расширяя класс прикладных задач, например [4], акцентируя внимание на развитие инновационных компонентов профессиональной компетентности, повышая соответствие учебного процесса требованиям современных образовательных и профессиональных стандартов. Важно, исследование дидактических и исследовательских возможностей информационных технология связано с реализацией перспективных направлений модернизации математической подготовки бакалавров [5].

Обратимся к результату, представленному на рис. 1. Найденные зависимости имеют вид при коэффициенте детерминации и при коэффициенте детерминации . Рис. 2 содержит следующие результаты эконометрического моделирования фондового рынка: зависимость при коэффициенте детерминации и зависимость при коэффициенте детерминации .

Проведенный анализ результатов моделирования позволяет разбить рассматриваемые финансовые инструменты на 3 группы по степени достоверности выявленных зависимостей (по возрастанию признака, коэффициент детерминации). К первой группе относится «Газпром» (). Ко второй группе относится «Аэрофлот» () и «ВТБ» (). К третьей группе относится «Магнит» ().

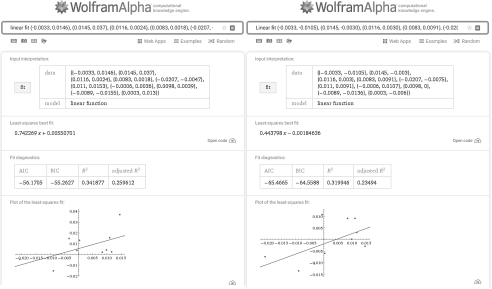
Рис. 1. Построение моделей Шарпа для финансовых инструментов «Аэрофлот» и «ВТБ»

Рис. 2. Построение моделей Шарпа для финансовых инструментов «Магнит» и «Газпром»

Результаты моделирования позволили выделить принципиальные различия в характере поведения рассматриваемых финансовых инструментов в зависимости от изменения доходности рынка в целом. Положительные угловые коэффициенты в уравнениях регрессионной зависимости, полученных для рассмотренных финансовых инструментов свидетельствуют, о том, что положительная динамика доходности рынка будет определять положительную динамику доходности этих финансовых инструментов. В случае падения доходности рынка в целом следует ожидать падение доходностей этих финансовых инструментов. В завершении статьи отметим, что новая база знаний и набор вычислительный алгоритмов WolframAlpha характеризуется высокими дидактическими и исследовательскими характеристиками, позволяет исследовать различные социально-экономические ситуации, расширяя представления студентов бакалавриата о количественных методах и математическом моделировании социально-экономических ситуаций, не располагающих к детерминированной трактовке.

Литература:

1. Власов Д. А. Технология визуализации проблем и ситуаций финансовой сферы // Педагогика высшей школы. — 2016. — № 2 (5). — С. 35–38.
2. Власов Д. А., Синчуков А. В. Интеграция информационных и педагогических технологий в системе математической подготовки бакалавра экономики // Современная математика и концепции инновационного математического образования. — 2016. — Т. 3. — № 1. — С. 208–212.
3. Власов Д. А., Синчуков А. В. Технологии WolframAlpha в преподавании учебной дисциплины «Эконометрика: базовый уровень» для студентов экономического бакалавриата // Вестник Российского университета дружбы народов. Серия: Информатизация образования. — 2016. — № 4. — С. 37–47.
4. Митрофанов В. И. Статистический анализ особенностей структуры Российского рынка акций // Статистика и экономика. — 2012. — № 5. — С. 127–133.
5. Синчуков А. В. Анализ перспективных направлений модернизации математической подготовки бакалавров // Инновационная наука. — 2016. — № 10–1. — С. 118–119.
6. Тихомиров Н. П., Дорохина Е. Ю. Эконометрика. — М.: Экзамен, 2003. — 512 с.
7. Тихомиров Н. П., Тихомирова Т. М. Риск-анализ в экономике. М.: Экономика, 2010. — 317 с.
8. Шарп У. Ф., Александер Г.Дж., Бэйли Дж.В. Инвестиции. — М.: Инфра-М, 2001. — 1028 с.