В статье рассмотрен практический пример оценки уровня конкуренции на рынке напольной плитки и мозаики. Предложенное решение позволяет графически отобразить конкуренцию на рынке.
Ключевые слова: кластерный анализ, анализ уровня конкуренции, дендрограмма.
Руководители одной из калининградских компаний, специализирующейся на продаже строительных и отделочных материалов, ощутили необходимость оценки уровня конкуренции на рынке напольной плитки и мозаики. Им был предложен вариант исследования уровня конкуренции на основе кластерного анализа. Кластерный анализ [1, с. 67] – это система инструментов классификаций многомерных наблюдений, основанных на определении понятия расстояния между объектами с последующим разбиением на группы, или кластеров. Выбор определенного инструмента кластерного анализа зависит от цели классификации. В данной статье рассмотрена графическая интерпретация данного метода – дендрограмма. В качестве исходных единиц анализа были взяты основные торговые центры строительных и отделочных материалов. При проведении исследования использовались следующие показатели: объем товарооборота; прибыль; средняя стоимость 1 м²; коэффициент обслуживания; продолжительность доставки (от производителя до покупателя). Исходные данные отражены в таблице 1.
Таблица 1
Исходные данные для анализа
|
Предприятие |
Объем товарооборота, млн руб. |
Прибыль, млн руб. |
Средняя стоимость 1 м², руб. |
Коэффициент обслуживания |
Продолжительность доставки (от производителя до покупателя), дней |
|
Конкурент А |
150 |
88 |
3000 |
0,2 |
1 |
|
Объект исследования |
84 |
30 |
6000 |
0,9 |
30 |
|
Конкурент Б |
99 |
26,5 |
10000 |
0,9 |
21 |
|
Конкурент В |
49 |
15,9 |
5000 |
0,6 |
14 |
|
Конкурент Г |
35 |
10,6 |
4000 |
0,5 |
30 |
|
Конкурент Д |
16 |
7,1 |
4000 |
0,4 |
14 |
|
Среднее |
72,17 |
29,68 |
5333,33 |
0,58 |
18,33 |
|
Вес критерия |
0,1 |
0,2 |
0,2 |
0,3 |
0,2 |
Исходные данные были преобразованы в матрицу (1) вида:
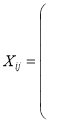
(1)
Далее производится расчет нормированных значений Z элементов, они фиксируются в виде матрицы, находятся по формуле (2), где столбцы j = 1,2,3,4 – это индекс показателя, строки i = 1,2, …, n – индекс наблюдателя;
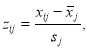(2)
; 
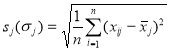(3)
Таким образом, получается матрица
(4), отраженная в таблице 2:
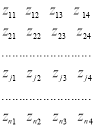
(4)
Таблица 2
Нормализованная матрица
|
Zij |
1.74 |
2.14 |
-1.02 |
-1.51 |
-1.71 |
|
0.26 |
0.01 |
0.29 |
1.24 |
1.15 | |
|
0.60 |
-0.12 |
2.04 |
1.24 |
0.26 | |
|
-0.52 |
-0.50 |
-0.15 |
0.07 |
-0.43 | |
|
-0.83 |
-0.70 |
-0.58 |
-0.33 |
1.15 | |
|
-1.26 |
-0.83 |
-0.58 |
-0.72 |
-0.43 |
В качестве «расстояния» между наблюдениями
и 
используют «взвешенное» евклидовое расстояние, которое определяется по формуле (5), где 
– вес показателя:
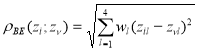, (5)
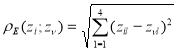(6)
Промежуточные расчеты евклидова расстояния отражены в таблице 3.
Таблица 3
Промежуточные расчеты
|
wi*(z1j-z2j)^2 |
0.22 |
0.90 |
0.34 |
2.27 |
1.63 |
2.32 |
|
wi*(z2j-z3j)^2 |
0.01 |
0.00 |
0.61 |
0.00 |
0.16 |
0.89 |
|
wi*(z3j-z4j)^2 |
0.13 |
0.03 |
0.96 |
0.42 |
0.10 |
1.27 |
|
wi*(z4j-z5j)^2 |
0.01 |
0.01 |
0.04 |
0.05 |
0.50 |
0.77 |
|
wi*(z5j-z6j)^2 |
0.02 |
0.00 |
0.00 |
0.05 |
0.50 |
0.75 |
|
wi*(z1j-z4j)^2 |
0.51 |
1.39 |
0.15 |
0.74 |
0.33 |
1.77 |
|
wi*(z1j-z5j)^2 |
0.66 |
1.61 |
0.04 |
0.42 |
1.63 |
2.09 |
|
wi*(z1j-z6j)^2 |
0.90 |
1.75 |
0.04 |
0.19 |
0.33 |
1.79 |
|
wi*(z2j-z4j)^2 |
0.06 |
0.05 |
0.04 |
0.42 |
0.50 |
1.03 |
|
wi*(z2j-z5j)^2 |
0.12 |
0.10 |
0.15 |
0.74 |
0.00 |
1.06 |
|
wi*(z2j-z6j)^2 |
0.23 |
0.14 |
0.15 |
1.16 |
0.50 |
1.48 |
|
wi*(z3j-z5j)^2 |
0.20 |
0.07 |
1.38 |
0.74 |
0.16 |
1.60 |
|
wi*(z3j-z6j)^2 |
0.34 |
0.10 |
1.38 |
1.16 |
0.10 |
1.75 |
|
wi*(z4j-z6j)^2 |
0.05 |
0.02 |
0.04 |
0.19 |
0.00 |
0.55 |
Рассчитанные значения фиксируются в виде матрицы расстояний (7):
; 
. (7)
Полученная матрица является симметричной R (), следовательно, можно отразить только наддиагональные значения. Полученные расстояния отражены в таблице 4.
Таблица 4
Матрица расстояний
|
1 |
2 |
3 |
4 |
5 |
6 | ||
|
rij |
0.000 |
2.317 |
2.464 |
1.769 |
2.088 |
1.790 |
1 |
|
0.000 |
0.886 |
1.033 |
1.056 |
1.477 |
2 | ||
|
0.000 |
1.275 |
1.597 |
1.755 |
3 | |||
|
0.000 |
0.774 |
0.547 |
4 | ||||
|
0.000 |
0.752 |
5 | |||||
|
0.000 |
6 |
Используя матрицу расстояний, можно осуществить идентичную иерархическую «цементирующую» процедуру кластерного анализа. Существует принцип «ближнего соседа» / «дальнего соседа» его используют для определения расстояния между полученными кластерами. В случае «ближнего соседа» – расстояние берется между ближайшими кластерами, в случае «дальнего соседа» между самыми удаленными друг от друга. Работа иерархических «цементирующих» процедур представляет собой последовательность действий по объединению элементов от ближайших к более удаленным друг от друга. В данном алгоритме на каждом шаге конкретное наблюдение (
) используется отдельным кластером. Далее объединяем два самых близких кластеров, затем строится новая матрица расстояний (размерность уменьшается на единицу) и итерация повторяется. Логика данной процедуры:p46=1 Кластеры (4) + (6); p456 = 2Кластеры (4) + (5) + (6);p23 = 3Кластеры (2+3);p23+456 = 4Кластеры (2+3) +(4+5+6);p1 + 23456 = 4Кластеры 1 +(2+3+4+5+6). В результате данных итераций – объединяющих строки и столбцы полученных кластеров – строится дендрограмма взаимодействия с учетом минимальных и пропорциональных условных «расстояний».
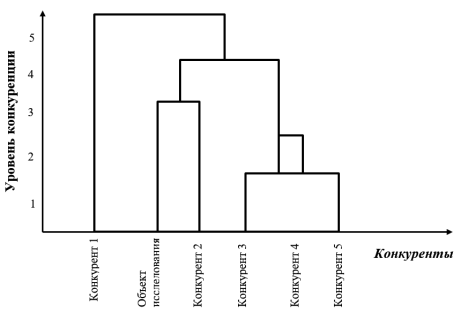
Рис. 1. Дендрограмма
Результаты кластерного анализа представлены на рис. 1 в виде дендрограммы, где по оси ординат отражены относительные «расстояния» показателей работы предприятий с учетом «весов» каждого из них. Данные расстояния между кластерами можно использовать как факторы необходимые для объединения в совместной деятельности с выгодой для себя и в ущерб конкурирующих предприятий. Проанализировав дендрограмму, можно сделать вывод, что на рынке лидирующее положение занимает «Конкурент 1», а объект исследования располагается на втором месте вместе с «Конкурентом 2».
Литература:
1. Левина Р.С. Кластерный анализ оценки конкуренции на рынке. Калининград: БГАРФ, 2007. – 27 с.
2. Левина Р.С. Планирование и прогнозирование в маркетинге / Р.С. Левина, Н.Ю. Лукьянова. Калининград: БФУ им. И. Канта, 2013. – 124 с.
