В статье рассмотрен математический алгоритм создания цифровой топологической модели железнодорожной станции в рабочем окне программы ИСУЖТ. Математический алгоритм построен на основе теории множеств, а также представлен пример отображения подмножеств с помощью кругов Эйлера. Разработаны этапы оцифровки топологических моделей станций и выявлено основное правило объединения элементов. Получено имитационное отображение схемы станции и описание технологии работы с помощью блок-схемы.
Интеллектуальная система моделирования железнодорожного транспорта функционирует на основе математического алгоритма условий, ограничений и последовательностей.
Бесперебойная работа программы обеспечивается за счёт соблюдения последовательности выполнения определенных математических операций. Для того, чтобы описать алгоритм выполняемых действий, необходимо ввести математические подмножества
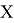
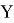
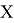
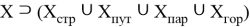
где:
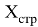
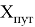
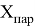
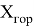
Значок
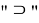
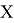
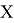
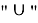
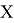
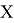
Описание подмножества
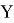
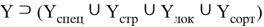
где:
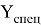
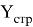
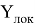
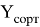
Чтобы наглядно представить объединение подмножеств
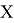
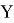
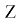
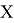
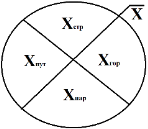
Рис. 1. Круг Эйлера, образующее множество инфраструктурных элементов
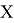
Правило объединения элементов между собой представлено записью:
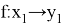
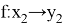
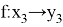
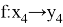
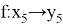
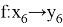
Тогда множество
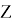
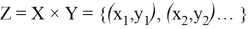
Для запуска математического цикла операций, необходимо загрузить данные из АС «ТРА». Вводим множество Z тра для сравнений подмножеств Х и У с нормативными подмножествами Х тра и У тра , где Х тра является подмножеством инфраструктурного назначения, а У тра — подмножеством технологического назначения. Совместно, подмножества Х тра и У тра образуют множество элементов Z тра , представленное формулой 4.
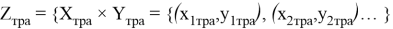
где:
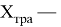
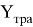
Множество элементов
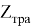
При загрузке данных происходит проверка на полное соответствие элементов множества Z с элементами множества
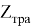
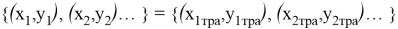
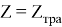
Если условие согласно формуле 5 не удовлетворено, то необходимо провести корректировку элементов с целью получения одинаковых размерностей инфраструктурного и технологического диапазонов множеств Z и
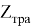
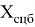
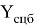
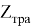
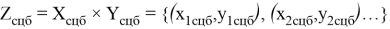
где:
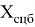
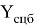
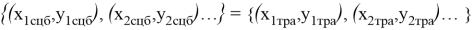
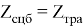
Представим, что на языке программирования «1» обозначает полное соответствие и удовлетворение математического условия ограничения, а «0» обозначает неудовлетворение математического условия и выявление ошибки. Таким образом, множества должны удовлетворить условию 8.
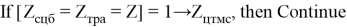
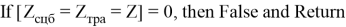
Удовлетворение условию 8 формирует множество элементов
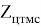
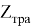
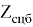
Результаты работы алгоритма показали, что данный инструмент может послужить платформой для разработки и получения цифровых топологических моделей железнодорожных станций. Можно произвести моделирование инфраструктурных и технологических процессов на станциях, что позволяет сократить трудозатраты на прогнозирование работы железнодорожных станций при изменении величин пассажиро- и грузопотока. Также алгоритм обеспечивает наглядное имитационное отображение всех происходящих процессов на станции и дает возможность заранее идентифицировать «узкие места».
В дальнейшем данный алгоритм подлежит дополнительной проработке для добавления динамики технологических процессов на цифровой топологической модели станции.
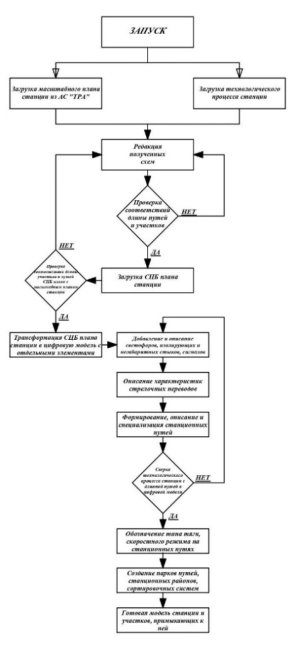
Рис. 2. Блок-схема, демонстрирующая основной принцип работы алгоритма цифровой топологической модели станции.
Литература:
- Александров П. С. Введение в теорию множеств и общую топологию. — М.: «Наука», Главная редакция физико-математической литературы, 1977.
- Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М. «Наука», Главная редакция физико-математической литературы, 1984.

