Под понятием кластеризации понимается процесс автоматического разбиения изначально заданного количества объектов на различные подгруппы, называемые кластерами, так, что два кластера не имеют между собой схожих свойств, а объекты, находящиеся в одной подгруппе, схожи.
Рассмотрим задачу кластеризации данных. Имеется выборка 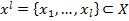 и функция, отображающая расстояние между объектами
и функция, отображающая расстояние между объектами 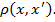 Алгоритм кластеризации — это функция
Алгоритм кластеризации — это функция 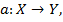 которая всем объектам
которая всем объектам 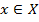 проставляет метку кластера
проставляет метку кластера 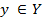 [1].
[1].
Основной идеей неиерархических алгоритмов кластеризации данных является минимизация расстояний между объектами в кластерах. Это происходит до тех пор, пока минимизирование расстояния между объектами становится невозможным.
Рассмотрим один из самых популярных и широко используемых методов кластерного анализа — алгоритм k–means (k–средних). В данном методе построение оптимального разбиения объектов на кластеры, определено как требование минимизации среднеквадратического отклонения на точках каждого кластера:
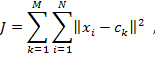 (1)
(1)
где
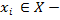 объект кластеризации (точка);
объект кластеризации (точка);
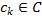 — центр кластера (центроид),
— центр кластера (центроид), 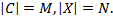
На момент начала работы алгоритма должно быть известно количество кластеров C, которые именно при первой итерации работы алгоритма будут считаться центрами кластеров. В дальнейшем будет проводиться перераспределение объектов по кластерам путем нахождения расстояния от каждой точки до центра кластера по наименьшему расстоянию. Евклидово расстояние является геометрическим расстоянием в многомерном пространстве и вычисляется по формуле:
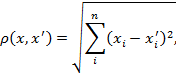 (2)
(2)
где
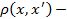 расстояние между объектами
расстояние между объектами 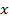 и
и 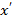 ;
;
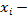 числовое значение
числовое значение 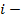 й переменной для объекта
й переменной для объекта 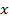 ;
;
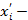 числовое значение
числовое значение 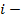 й переменной для объекта
й переменной для объекта 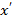 ;
;
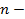 число переменных, которыми описываются объекты (или количество данных характеристик) [3].
число переменных, которыми описываются объекты (или количество данных характеристик) [3].
После того как все объекты распределены по кластерам, заново считаются центры масс кластеров по формуле:
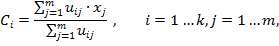 (3)
(3)
где
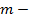 количество набора кластеров в результате кластеризации;
количество набора кластеров в результате кластеризации;
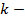 количество начального набора кластеров;
количество начального набора кластеров;
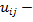 коэффициент принадлежности.
коэффициент принадлежности.
Определения коэффициента принадлежности объекта к определенному кластеру, которая считается по формуле:
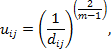 (4)
(4)
где
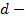 расстояние от объекта до центра кластера;
расстояние от объекта до центра кластера;
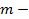 коэффициент неопределенности,
коэффициент неопределенности,
Перераспределение объектов по кластерам и пересчет центра масс каждого кластера проводится до тех пор, пока кластерные центры не стабилизируются, то есть если 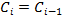 , либо пока не наступит момент, когда ни одна из данных точек не перейдёт к соседнему кластеру на текущей итерации.
, либо пока не наступит момент, когда ни одна из данных точек не перейдёт к соседнему кластеру на текущей итерации.
К достоинствам данного алгоритма можно отнести простоту реализации, понятность и прозрачность, а так же приемлемую сложность 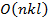 , где
, где 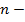 множество объектов,
множество объектов, 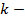 количество кластеров,
количество кластеров, 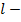 число итераций алгоритма.
число итераций алгоритма.
Недостатками алгоритма являются зависимость результата от инициализации центров кластеров и неопределенность выбора начального количества точек, играющих роль центров кластеров при первой итерации [2].
Далее вводится метрика, которая позволит оценить качество распределения элементов выборки по кластерам, полученное в результате работы алгоритма, относительно ожидаемого (иначе говоря, правильного) разбиения, задаваемого при проектировании набора данных.
Определим понятия точности и полноты полученного кластера 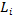 относительно ожидаемого кластера
относительно ожидаемого кластера 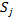 :
:
- точность:
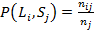 ;
;
- полнота:
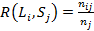 ,
,
где
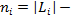 число элементов в кластере
число элементов в кластере 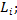
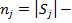 число элементов в кластере
число элементов в кластере 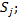
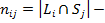 число общих элементов
число общих элементов 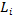 и
и 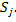
Введем для пары 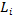 и
и 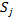
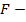 меру как среднее гармоническое точности и полноты:
меру как среднее гармоническое точности и полноты:
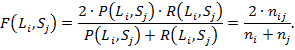 (5)
(5)
Далее определим 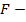 меру
меру 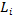 относительно ожидаемого разбиения
относительно ожидаемого разбиения 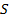 как максимальное значение
как максимальное значение 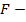 мер
мер 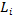 относительно кластеров из разбиения
относительно кластеров из разбиения 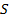 :
:
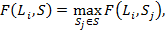 (6)
(6)
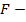 меру всего полученного разбиения
меру всего полученного разбиения 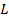 относительно ожидаемого будем считать как взвешенную сумму
относительно ожидаемого будем считать как взвешенную сумму 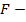 мер для каждого из полученных кластеров:
мер для каждого из полученных кластеров:
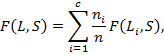 (7)
(7)
где 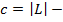 количество кластеров в разбиении
количество кластеров в разбиении 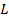 ;
;
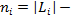 число элементов в кластере
число элементов в кластере 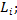
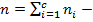 общее число элементов в выборке.
общее число элементов в выборке.
Чем 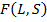 больше, тем ближе полученное разбиение к ожидаемому разбиению. В лучшем случае, когда каждому кластеру из
больше, тем ближе полученное разбиение к ожидаемому разбиению. В лучшем случае, когда каждому кластеру из 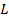 отвечает ровно один из
отвечает ровно один из 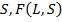 обращается в единицу [4].
обращается в единицу [4].
Наконец, определим 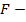 меру системы
меру системы 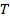 вложенных разбиений данной выборки на кластеры относительно ожидаемого распределения
вложенных разбиений данной выборки на кластеры относительно ожидаемого распределения 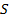 как
как 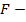 меру наилучшего разбиения из системы
меру наилучшего разбиения из системы 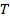 :
:
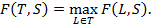 (8)
(8)
Одним из подходов определения оптимального количества кластеров является анализ индексов Калинского-Харабаза (Caliński–Harabasz index). Для этого необходимо найти такое количество кластеров, которое максимизировало бы функцию, представленную в формуле:
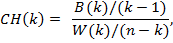 (9)
(9)
где
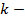 количество кластеров;
количество кластеров;
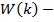 матрица внутренней дисперсии;
матрица внутренней дисперсии;
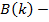 матрица внешней дисперсии.
матрица внешней дисперсии.
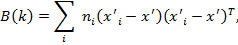 (10)
(10)
где
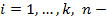 количество объектов в изучаемых данных.
количество объектов в изучаемых данных.
Наиболее вероятным количеством кластеров является значение 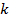 , на котором индекс
, на котором индекс 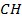 достигает максимальное значение [4].
достигает максимальное значение [4].
Алгоритм k-means является простым итеративным алгоритмом кластеризации, разделяющим множество данных на k кластеров. По своей сути, алгоритм работает с помощью перебора в два этапа: 1) кластеризация всех точек данных в зависимости от расстояния между точкой и ее ближайшим представителем кластера; 2) переоценка представителей кластера. Ограничения алгоритма k-means включает чувствительность k-means к инициализации и определению значения k.
Несмотря на все недостатки, k-means остается наиболее широко используемым разделяющим алгоритмом кластеризации на практике. Алгоритм простой, понятный и достаточно масштабируемый и может быть легко модифицирован для решения различных задач, таких как частичное обучение с учителем или потоковых данных. Постоянные улучшения и обобщения основных алгоритмов обеспечили его актуальность и постепенное увеличение эффективности.
Литература:
1. Кутуков Д. С. Применение методов кластеризации для обработки новостного потока / Д. С. Кутуков // Технические науки: проблемы и перспективы: материалы междунар. науч. конф. (г. Санкт-Петербург, март 2011 г.). — СПб.: Реноме, 2011. — с. 77–83.
2. Кондратьев М. Е. Анализ методов кластеризации новостного потока. — Труды 8-й Всерос. науч. конф. «Электронные библиотеки: перспективные методы и технологии.
3. Баргесян А. А., Куприянов М. С., Степаненко В. В., Холод И. И. Методы и модели анализа данных: OLAP и Data Mining. — СПб.: БХВ-Петербург, 2004. — 336 с.
4. Сокэл Р. Р. Кластерный-анализ и классификация: предпосылки и основные направления. В кн: Классификация и кластер /Под ред. Дж.Вэн Райзина М: Мир, 1980, с.7–19.







