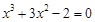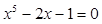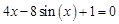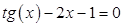Численные методы — это раздел математики, содержащий методы решения математических задач в численном виде: разработка, обоснование и реализация (на базе вычислительной техники) методов приближенного решения разнообразных задач на уровне математических моделей. В основе численных методов лежат алгоритмические схемы переработки информации с целью нахождения приближенного решения рассматриваемой задачи в числовой форме. Численные методы являются основным инструментом решения современных прикладных задач. Аналитическое решение задачи можно найти далеко не всегда в силу сложного, как правило, нелинейного, вида систем уравнений, описывающих задачу. Поэтому численный анализ математических моделей — метод решения, алгоритм, программа, вычислительный эксперимент — является в настоящее время наиболее эффективным аппаратом исследования прикладных проблем [1,2].
Следует также подчеркнуть компьютерно-ориентированный характер численных методов в конечном итоге их реализация связана с применением вычислительной техники и программирования. Естественно, что прогресс в области вычислительной математики в немалой степени обусловлен новыми возможностями в развитии компьютерных ресурсов. Однако даже сравнительно высокая производительность современных компьютеров не снимает проблему разработки эффективных и экономичных в плане вычислительных затрат методов решения, специализированных для определенных классов задач. Проблема оптимизации (модификации, модернизации) вычислительных методов по-прежнему сохраняет свою актуальность и определяет перспективу дальнейшего развития численного анализа.
При обучении студентов численным методам основными формами занятий являются лекции и лабораторные работы. Лабораторная работа является активной формой обучения, использующей различные информационные технологии.
Надо отметить, что в любом фундаментальном учебнике по численным методам основной объем занимают не алгоритмы и вычислительные схемы, а строгие обоснования используемых методов, получение оценок решения, сходимости метода и его устойчивости. Это объясняется тем, что вычислительная математика строгая математическая дисциплина, которая появилась задолго до компьютеров и информатики. Но при получении решения прикладной задачи с использованием компьютерных технологий на первый план выступают вопросы выбора методов решения, их алгоритмизации и программирования.
Таким образом, курс «Численные методы», с одной стороны, излагает математическую теорию методов вычислений, с другой — аккумулирует возможности компьютерных информационных подходов для изучения процессов и явлений реальной действительности в ходе инженерной практики.
Однако существующая практика обучения численным методам в вузе показывает, что обучение студентов основано на изучении определенного количества задач разного типа, так называемых классических задач, с использованием разных методов и средств. Такой подход позволяет эффективно обучать решению только типовых задач, вошедших в учебную программу.
При выполнении лабораторных работ нередко используется программирование численных методов на современных алгоритмических языках. Этот подход, во-первых, является традиционным, а, во-вторых, усиливает активность студентов при изучении методов. За многие годы накоплены обширные библиотеки научных подпрограмм на различных алгоритмических языках, предназначенных для решения типовых задач вычислительной математики.
В образовательный процесс, наряду с классическим подходом к проведению лабораторных работ по численным методам (программирование вычислительных алгоритмов и их реализация с помощью компьютерных средств) в настоящее время применяются различные компьютерные математические пакеты (Maple, Mathematica, MathLab, MathCad и др.) [3,4]. Данные пакеты предназначенные для автоматизации решения математических задач в различных областях науки, техники и образования, интегрирующие в себе современный интерфейс пользователя, систему аналитических, численных методов решения достаточно широкого класса математических задач, средства визуализации результатов вычислений, что на стадии принятия управленческих решений позволяет с большей достоверностью проанализировать полученные результаты, в том числе дать им содержательную экономическую интерпретацию
Использование возможностей математических пакетов не лишают студента возможности создания собственных программ, реализующих численные методы. Так как большинство пакетов имеют встроенные алгоритмические языки. Таким образом, в одном файле студент получает, как минимум, решение задачи тремя способами, которые можно сопоставить, провести оценку погрешности и сделать выводы об эффективности методов.
Еще один аргумент в пользу использования математических пакетов — отсутствие необходимости хорошего владения алгоритмическими языками. Алгоритмическая культура формируется довольно длительно, а дисциплина «Численные методы» изучается на младших курсах. Значительная часть времени лабораторных работ при использовании алгоритмических языков отводится отладке программ, а не исследованию параметров алгоритмов и их эффективности. Математические пакеты в разной степени отвечают требованиям вычислительной среды при изучении численных методов. Для проведения лабораторных работ по данной дисциплине сформированы следующие требования к инструментарию вычислительной среды: привычные стандартные математические обозначения, среда визуального программирования, возможность символьных вычислений, понятный интерфейс пакета, относительная непритязательность к возможностям компьютера.
Тем не менее, следует отметить, что программная реализация вычислительных алгоритмов с помощью компьютерных средств позволяет студентам более глубоко усвоить фундаментальные основы теории и методологии нахождения приближенных решений математических задач. В процессе обучения численным методам на лабораторных работах целесообразно применяются различные информационные технологии.
В результате изучения курса численных методов студент должен не только получить фундаментальные математические знания по этой дисциплине, но и повысить свои основные навыки в применении новейших компьютерных технологий применительно к вычислительной математике. Таким образом, можно сделать вывод, что «Численные методы» можно и нужно изучать в два этапа, вначале с помощью любого математического пакета, а после того как студенты поймут суть методов, можно переходить к их программированию.
Мною разработано учебно-методическое пособие «Численные методы», предназначенное для студентов всех форм обучения направления подготовки «Прикладная информатика» Рубцовского института (филиала) алтайского государственного университета. Оно посвящено изложению основ численных методов решения задач алгебры, математического анализа, обыкновенных дифференциальных уравнений и реализации этих методов в современном математическом пакете Maple. Пособие содержит разделы «Элементы общей теории приближенных методов», «Методы решения систем линейных алгебраических уравнений», «Методы решения нелинейных уравнений и систем», «Аппроксимация и интерполяция функций», «Численное дифференцирование», «Численное интегрирование», «Численные методы решения обыкновенных дифференциальных уравнений», «Основы Maple». Темы заканчиваются заданиями к соответствующим лабораторным работам, каждая из которых снабжена 20 вариантами индивидуальных заданий. Типовые задачи даны с подробными решениями.
Каждый его раздел включает: необходимый теоретический материал, блок-схемы вычислительных алгоритмов, с составлением которых у студентов чаще всего связаны основные трудности и большое количество примеров решения практических задач с использованием современного математического пакета Maple.
Использование такого пособия на лабораторных занятиях по численным методам позволяет студентам с различным уровнем подготовки и индивидуальными особенностями выполнять необходимые задания; способствует формированию у них представления о фундаментальных основах теории и методологии вычислений, высокого уровня знаний, умений и навыков, необходимых для численного решения прикладных задач, анализа, сравнения, обобщения полученных результатов.
Приведем пример лабораторной работы «Методы отделения корней уравнений с одной переменной»
Цель работы: Освоение различных численных методов решения нелинейных уравнений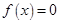 
. Решение проблемы отделения корней на отрезке. Подробное изучение различных методов для уточнения корня уравнения. Получение навыков решения задач вычислительной математики на ЭВМ.
Задание:
1. Отделите корни трансцендентного уравнения графически, используя математический пакет Maple.
2. Решите уравнение в математическом пакете Maple с помощью встроенных функций.
3. Напишите программу приближенного вычисления корня уравнения 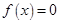методом половинного деления, Ньютона, простых итераций и хорд. В программе задается точность вычисления 
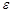, начальное приближение 
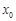или отрезок 
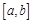; выводится результат решения 
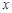и число итераций 
.
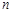4. Проведите сравнительную характеристику методов. Сравните число итераций до достижения заданной точности в различных методах.
5. Ответьте на вопросы.
Варианты заданий:
|
№ |
Задание |
|
Задание |
|
1 |
|
3 |
|
|
2 |
|
4 |
|
|
|
… |
|
… |
Таким образом, использование математического пакета Maple в учебном процессе позволяет перейти на новый, более глубокий и качественный уровень преподавания дисциплины «Численные методы».
Литература:
1. Срочко, В. А. Численные методы. Курс лекций / В. А. Срочко — изд. 1-е стер. — М.: Лань, 2010. — 208 c.
2. Бахвалов, Н. С. Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков — изд. 7-е — М.: Бином. Лаборатория знаний, 2012. — 636 c.
3. Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах Mathcad 12, Matlab 7, Maple 9/ — М.: НТ Пресс, 2006. –496с (самоучитель).
4. Дьяконов В. П. Mathematica 5.1/5.2/6. Программирование и математические вычисления. — М.: ДМК_Пресс, 2008. — 576 с.
