Тәуелсіздік алған Қазақстан Республикасы үшін елдің ертеңі жарқын, болашағымыз кемелді, ұрпағымыз сауатты болуы үшін әрине еліміздің дамуының басқа бағыттарымен қатар білім саласы да ерекше маңыздылыққа ие болуы қажет. Білім берудің бүгінгі күнгі талабы- оқушының жан-жақты іс-әрекеттік қабілетінің дамуы. Оқушыны дамытуда ежелгі замандардан бері математиканың алар орны ерекше. Математика ғылымының өзге ғылымдар мен техниканың қарқынды дамуына қосар үлесі аз болған жоқ. Математика – барлық ғылымдардың логикалық негізі болғандықтан да математика- оқушының дұрыс ойлау мәдениетін қалыптастырады, дамытады, оны шыңдай түседі, оған қоса өзге салаларды дұрыс қабылдауға көмек береді.
Математикалық логиканы жетік түсінбейінше, оны меңгеру өте қиын. Себебі қазіргі кезде ғылым мен техника қарыштап дамыған сайын ол адамның ойлау қабілетінің ең ірі жетістіктері болып табылады.
Математикадағы комбинаторика көптеген логикалық есептерді оңай жолдармен шығаруға, есептерді шешуде және олардың шығару жолдарын адам есіне лезде сақтап қалу үшін де көмектеседі. Логикалық есептер адамның ойлау қабілетінің дамуына әсер етеді және арттырады. Сондай-ақ комбинаторлық есептерде теңдеуді шешуге, өрнекті ықшамдауға, теңдікті дәлелдеуге болады.
Комбинаторлық әдістер физика, химия, биология, экономика, тағы басқа ғылымда қолдануға болады.Саны шектеулі элементтерден әртүрлі комбинациялар құрастыруға және белгілі біререже бойынша құрастырылған барлық мүмкін комбинациялар санын есептеуге туракелетін жағдайлар жиі кездесіп отырады. Мұндай есептер комбинаторлық есептер, ал оларды шешумен шұғылданатын математика бөлімі комбинаторика деп аталады. Көптеген комбинаторлық есептерді шешу үшін қосынды және көбейтінді ережелерін қолданады. Комбинаторика есептерін шешуде қолданатын өзіндік заңдылықтар мен формулалар бар.
Төменде қарастырылған комбинаторлық есептерді шешу жолдарын қарастыралық.
1.Теңдеуді шешу керек:
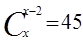
Шешуі: Теңдеуді шешу барысында терулердің формуласын
= 
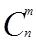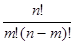(1)
пайдаланып, 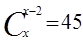келесі түрде жазамыз:
=
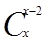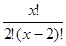
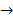
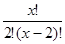=45алдымен теңдіктің сол жағын түрлендіріп аламыз,
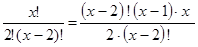
Сосын алынған түрлендіруді теңдіктің оң жағындағы санға теңестіргенде:
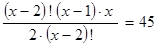
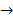
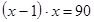
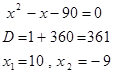
Теңдеудің шешімі ретінде оң мәнді аламыз, яғни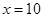 
болады.
Жауабы: .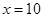
2. Өрнекті ықшамдау: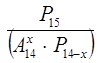
Шешуі: Берілген өрнекті шешу мақсатында орналастырулардың формуласы:
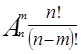(2)
Жәнеалмастырулардыңформуласы: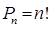 
(3)
Демек, (2) және (3) формулаларды пайдалансақ, төмендегі нәтиже шығады:
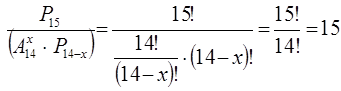
Жауабы: 15.
3.Теңдікті дәлелдеу: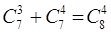 
Теңдікті ділелдеу үшін (1) формуланы қолданамыз. Сонда былай жазылады:
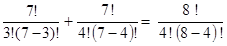
Теңдіктің екі жағын жеке-жеке шешейік,
1) 
,
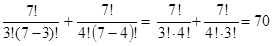2) 
.
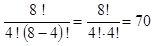Осыдан теңдіктің екі жағының тең екендігіне көзіміз жетті. Демек, 70 = 70.
Математика- оқушының дұрыс ойлау мәдениетін қалыптастырады, дамытады, оны шыңдай түседі, оған қоса өзге салаларды дұрыс қабылдауға көмек беретіндігін ескере отырып, жоғарыда қарастырылған есептер оқушының пәнге деген қызығушылын арттырады деп қорытындылай аламыз. Білімге, дағдыға, ептілікке үйрететінін атап көрсетуге болады.Сондықтан комбинаторика алған математикалық білімін нақты қолданатын, адам өмірінде маңызы зор математиканың бір тарауы ретінде қарастырылады.
Әдебиет:
1. Жаңбырбаев Б.С., Добрица В.П. Математикалық логиканың бастамалары: Оқу құралы – Алматы: Абай атындағы АлМУ, 2001.
2. Ершов Ю.Л., Палютин Е. А. Математическая логика. - СПб.: Лань, 2004.
3. Игошин А.А. Математическая логика, теория алгоритмов. - М., Академия, 2004.
4. Хаггарти Р. Дискретная математика для программистов: Пер.с англ. – М.: Техоссфера, 2003. -320 с.
