Формализация процедуры выбора оптимальной структуры организации

Теория организационного управления предоставляет разработчикам систем управления (СУ) социально-экономическими объектами (СЭО) различные структуры организации, отличающиеся по ряду признаков: степень централизации власти, характер распределения функций и ресурсов, целый спектр корпоративных культур и т.д.  В данном признаковом пространстве можно выделить несколько видов эталонных структур: иерархическая, матричная, дивизиональная и пр. С целью формализации задачи выбора подходящей структуры обозначим их символом s_i , где индекс i – номер структуры, изменяется от 1 до n. Кортеж

S=(s₁, s₂, …, s_n)                                                   (1)  

представляет собой полный перечень возможных для реализации альтернативных структур организации.

Оцениваются структуры экспертами – специалистами  в области корпоративного управления. На первом этапе определяется перечень критериев оценки. Например: с₁ – степень адаптивности структуры к изменению условий среды функционирования организации, с₂,с₃ – управленческая эффективность (скорость и точность достижения управленческих целей), с₄  – экономическая эффективность (затратность) и т.д. Кортеж

С=(с₁, с₂, …, с_m)                                                   (2)  

определяет полный перечень критериев оценки структуры организации.

Для оценки альтернатив по векторному критерию иногда применяются преобразования, переводящие многокритериальную задачу в однокритериальную [1]:

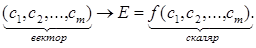
Наиболее распространенными схемами перевода векторного критерия в скалярный вид являются свертки: аддитивная и мультипликативная. Для применения этих методов необходимо знать ответы на следующие непростые вопросы: как определить вид функции свертки f ? Как назначить веса критериев в этой функции? Как измерять качественные критерии? Какова чувствительность многокритериального выбора к изменениям весов критериев? Кроме того, при использовании свертки критериев эффекты компенсируются и вариант решения «плохой» по одному критерию может быть «вытянут» в «хорошие» другим. Эти проблемы требуют использования современных схем многокритериальной оптимизации, учитывающих условия функционирования социально-экономических систем [1].

Специфика объекта исследования (СЭО) не позволяет дать точные априорные оценки вариантов s_i по заданным критериям (2): априорной информации, как правило, у лица, принимающего решения (ЛПР) – нет, статистика о предыдущих периодах функционирования СЭО отсутствует или нестационарная. Имеется единственный способ –  использовать опыт и интуицию специалистов. Это подход требует учесть и рассмотреть несколько аспектов.

В моделях принятия решений в условиях неопределенности широкое распространение получил принцип Беллмана-Заде [2], согласно которому оптимальная альтернатива ищется в соответствие со следующим алгоритмом:

1) каждый критерий с_i представляется в виде нечеткого множества, заданного на универсальном множестве альтернатив S (1);

2) путем пересечения нечетких множеств-критериев образуется множество потенциально хороших решений? То есть, решений, одновременно удовлетворяющих всем критериям (рис. 1);

3) в нечетком множестве потенциальных решений выбирается альтернатива с наибольшей степенью принадлежности, она и есть оптимальное решение.

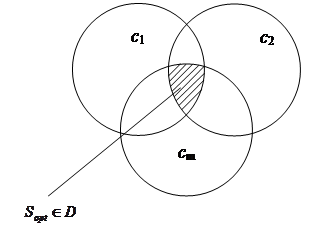
Рис. 1. Множество потенциально хороших решений

Принцип Беллмана-Заде [2], как правило, применяется совместно с методом иерархий Т. Саати [3], что позволяет находить степени принадлежности элементов нечетких множеств с  помощью процедуры парных сравнений вариантов. Соответствующая методика подробно описана в [4]. Метод иерархий [3, 5] предусматривает формирование матрицы парных сравнений, проверку ее согласованности и отыскание собственного вектора, который определяет искомые степени принадлежности. Если согласованность матрицы отсутствует, то процедура парных сравнений должна выполняться заново, что усложняет практическое применение метода.

В работе [6] предложена модификация метода Т. Саати, не требующая нахождения собственного вектора и проверки согласованности матрицы парных сравнений. Методика многокритериального выбора альтернатив, использующая модифицированный метод Т. Саати [6], рассмотрена в [7]. Процедура формирования матрицы парных сравнений является достаточно трудоемкой  из-за наличия в ней дробных элементов, не входящих в девятибалльную шкалу Т. Саати.

В статье [1] предлагается метод, основанный на идеях Беллмана-Заде и Т. Саати, но не требующий формирования парных сравнений. Вместо этого применяются простые расчетные соотношения, содержащие сравнения с наихудшей альтернативой и наименее важным критерием. Отсюда название разработанного метода: «Метод наихудшего случая». В качестве иллюстративного примера в [1]  рассматривается задача выбора подходящего автомобиля из перечня заданных вариантов. Ниже, предложенная технология многокритериального выбора, адаптируется к решению задачи выбора оптимальной структуры организации. Рассмотрим основные положения этой теории.

1. Представление критериев в виде нечетких множеств. Каждый критерий 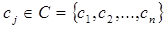 будем интерпретировать как нечеткое множество, заданное на универсальном множестве альтернатив  в виде

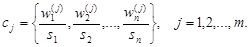                               (3)

Соотношение (3) называется функцией принадлежности нечеткого множества. Под чертой указывается исследуемый объект, над чертой – его вес. Входящие в (3) степени принадлежности 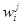 элементов  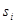к нечетким множествам представляют собой числа в интервале [0, 1], которые могут рассматриваются как веса альтернатив относительно критериев 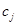. Потребуем выполнения естественного условия

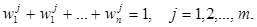
2. Выбор наилучшей альтернативы. Согласно принципу Беллмана-Заде, наилучшую альтернативу s_opt будем искать внутри пересечения (∩) нечетких множеств-критериев (рис. 1), т.е.

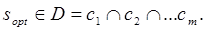
В теории нечетких множеств имеет место замена операций: ∩ → min. Поэтому множество потенциально хороших решений выглядит так

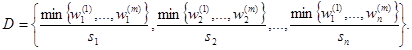              (4)

В качестве наилучшей альтернативы s_opt следует выбирать альтернативу 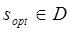 c максимальным весом

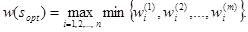                                                   (5)

В научно-методической литературе данная технология принятия решений известна также как максиминная или гарантированная стратегия.

Таким образом, задача выбора оргструктуры СЭО свелась к задаче идентификации весов альтернатив.

3. Определение весов альтернатив. Предполагается метод определения весов альтернатив, входящий в нечеткие множества (3). Идея метода автором [1] заимствована из структурного анализа систем [8], где надежность системы распространяется между ее элементами в соответствии с рангами. Ранг элемента характеризует его важность в смысле надежности. Чем выше ранг, тем выше надежность. В нашем случае сумма весов, равная единице, будет распределяться между альтернативами согласно их рангов.

Пусть r_i – ранг альтернативы 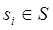 в отношении критерия 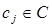. Индекс этого критерия в обозначении ранга не указывается для упрощения записи. Будем предполагать следующее: чем выше вес w_i альтернативы, тем выше ее ранг r_i. Это предположение формализуется соотношением:

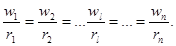                                                       (6)

Пусть s_l – наихудшая альтернатива (по критерию 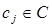) с весом w_l и рангом r_l. Используя соотношение (6), выразим веса всех альтернатив через вес наихудшей альтернативы

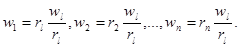                                              (7)

Подставляя веса (7) в условие 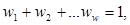 получим вес наихудшей альтернативы

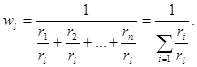                                             (8)

Соотношения (7) и (8) позволяют вычислить искомые веса альтернатив через отношения рангов всех i-х альтернатив к рангу наихудшей l-й альтернативы. Заметим, что сравнение с наихудшим случаем обеспечивает выполнение условия 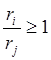  для всех i = 1, 2, …, n.

Для сравнения альтернативных структур необходимо установить отношения их рангов. Саати Т. предложил [2], и практика уже подтвердила адекватность этой позиции, следующую таблицу отношений рангов:

                                 (9)

В предыдущих рассуждениях все критерии предполагались равнозначными. На практике при управлении СЭО ситуация меняется: в зависимости от условий функционирования организации важность критериев изменяется.

5. Механизм учета важности критериев. Пусть α_j – вес критерия 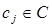, характиризующий его важность. С учетом весов критериев нечеткое множество решений формируется так [2]:

,

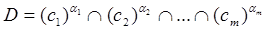где c_j – нечеткие множества (3), j = 1,2, …, m. Если α₁ = α₂ = … α_m = 1, то получаем случай одинаковой важности критериев, рассмотренный выше. Для определения весов α_j также как и для весов альтернатив ранее использовалась достаточно трудоемкая техника парных сравнений [4-6]. Автор [1] предлагает сравнивать критерии с наименее важным из них.

Будем предполагать, что чем выше вес α_j критерия 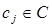, тем выше его ранг R_j т.е.

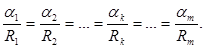
Пусть α_k и R_k – вес и ранг наименее важного критерия соответственно. Требуя выполнения условия α₁ + α₂ + … + α_k = 1,  по аналогии с процедурой определения весов альтернатив, распределим веса критериев согласно их рангам.

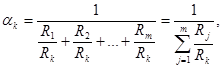                                      (10)

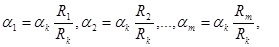                                    (11)

где отношения рангов критериев оцениваются девятибалльной шкалой.

Рассмотрим конкретный пример выбора одной из четырех заявленных альтернатив при синтезе структуры организации: s₁ - иерархическая, s₂ - функциональная, s₃ – матричная, s₄ – дивизиональная. В качестве равнозначных критериев выбора рассматриваются:  с₁– степень адаптивности структуры к изменению условий среды функционирования организации, с₂ – управленческая эффективность, с₃ – экономическая эффективность.

Построим функции принадлежности (3) заданных критериев.

Критерий с₁. По этому критерию наихудшей альтернативой, очевидно, является s₁. Согласно мнению эксперта, а также соотношениям (8) и (9) ее вес равен:

w₁ = 1/(1+5+9+7) = 1/22.

Это получено на основе следующих мнений эксперта: «s₁совпадает с s₁», «s₂ лучше, чем s₁», «s₃ абсолютно лучше, чем s₁» и «s₄ значительно  лучше, чемs₁». Веса остальных критериев согласно (7) равны: w₂ = 5/22,  w₃ = 9/22,w₄ = 7/22.

Критерий с₂. Аналогично предыдущему, считая худшим вариант s₃, получаем: w₃ = 1/(7+5+1+5) = 1/18. Тогда: w₁ = 7/18,  w₂=5/18, w₄ = 5/18.

И, наконец, критерий с₃. По этому критерию худшим эксперт принимаем вариант дивизиональной структуры s₄. Несложные расчеты дают: w₄ = 1/(7+6+2+1) = 1/16. Тогда: w₁ = 7/16,  w₂ = 6/16,w₃ = 2/16.

Операция (4) дает совокупность значений (1/22, 5/22, 1/18, 1/16) – минимальные веса по альтернативам. Максимальное из этих значение равно 5/22, поэтому, согласно (5) оптимальным вариантом структуры является s₂ . Это функциональная структура организации.

Литература:

1.                  Ротштейн А.П. Нечеткий многокритериальный выбор альтернатив: метод наихудшего случая // Теория и системы управления, 2009, № 3.

2.                  Bellman R., Zadeh L. Decision Making in Fuzzy Environment // Management Science. 1970. V. 17.

3.                  Саати Т. Математические методы конфликтных ситуаций. М.: Сов. Радио, 1977.

4.                  Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей: Примеры использования. Рига: Зинатне, 1990.

5.                  Саати Т., Кернс К. Аналитическое планирование. Организация систем. М.: Радио и связь, 1991.

6.                  Rotshtein A.P. Modification of the Saaty Method for the Construction of  Fuzzy Set Membership Functions // Proc. Inf. Cont. on Fuzzy Logic and Its Application. Israel, 1997.

7.                  Ротштейн А.П., Штовба С.Д. Нечеткий многокритериальный анализ вариантов с применением парных сравнений // Изв. РАН ТиСУ. 2001. №3. С. 150-154.

8.                  Нечипоренко В.И. Структурный анализ систем: надежность и эффективность. М.: Сов. радио, 1976.