Прикладная направленность курса математики в строительном вузе

Математика в строительном вузе является одним из общеобразовательных предметов, изучаемых на первых курсах. Целью математического образования является получение математических знаний и выработка умения применять эти знания либо в решении прикладных задач, либо в строительстве и перестройке самого постоянно развивающегося здания математики. Поскольку научить рецептам решения всех задач, встречающихся специалисту в его работе невозможно, то важно выработать культуру мышления, умение творчески подходить к решению возникающих задач. Таким образом, имеется тенденция усиления прикладной направленности курса математики и, одновременно, повышения уровня фундаментальной математической подготовки.

Основные цели, стоящие перед математическим образованием охарактеризуем следующим образом. Выпускники вузов должны уметь в пределах своей специальности: 1) строить математические модели; 2) ставить математические задачи; 3) выбирать подходящий математический метод и алгоритм для решения задачи; 4)применять для решения задачи численные методы с использованием современных вычислительных машин; 5) применять качественные математические методы исследования; 6) на основе проведенного математического анализа вырабатывать практические выводы.

Получаем, что целью обучения математике является приобретение учащимися определенного круга знаний, умения использовать изученные математические методы, развитие математической интуиции, воспитание математической культуры. Упражнение в математике содействует приобретению рациональных качеств мысли и ее выражения: порядок, точность, ясность, сжатость. Исходя из этого, математика предоставляет широкие возможности для формирования профессиональных качеств личности инженера — строителя, тем самым подчеркивая ее фундаментальную значимость.

Профессиональные характеристики личности инженера — строителя, формируемые при обучении математике, определяются требованиями, предъявляемыми к математической подготовке специалиста данного профиля профессиональной деятельностью. Эти требования зафиксированы в Государственном образовательном стандарте высшего профессионального образования по направлению «Строительство».

Согласно Государственному стандарту, основными требованиями к математической подготовке инженера — строителя являются: твердое усвоение фундаментальных понятий (предел, непрерывность и т. д.) математики; понимание приводимых в курсе математики доказательств; усвоение основных математических фактов, формул; понимание связи математических моделей с моделируемыми материальными явлениями; усвоение навыков решения математических задач, в частности, навыков приближенных вычислений; правильное истолкование полученных результатов в применении к практическим приложениям.

Вышеприведенные требования к математической подготовке инженера — строителя предполагают не только вооружение студентов определенным набором математических знаний и методов, но и предусматривают рассмотрение их практических приложений. Для того чтобы успешно использовать математический аппарат в практике профессиональной деятельности будущий инженер — строитель должен обладать следующими качествами: 1) владеть взаимосвязанным представлением о содержании математического образования и содержании дисциплин строительного профиля; 2) иметь представление о математике как о средстве профессионального совершенствования своей личности; 3) обладать основными интеллектуальными умениями (как общематематичекими, так и специфическими), необходимыми инженеру–строителю для решения профессиональных задач.

Именно на развитие данных качеств будущего строителя и должна быть направлена работа педагога по математике. Для этого необходимо при изучении каждой математической темы рассматривать блок задач по ее применению, содержащихся в непосредственной практике, студента какой-либо специальности.

Например, изучаю тему «Интегральное исчисление» можно рассмотреть задачи: 1. По опытным данным зависимости энтропии s от температуры процесса Т:

Определить среднеинтегральную температуру газа Т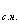, используя для этого термодинамическое соотношение:.

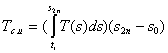2. С помощью подъемного крана извлекают железобетонную надолбу со дна реки глубиной 5м. Какая работа при этом совершается, если надолба имеет форму правильного тетраэдра с ребром 1 м.?

Плотность железобетона 2500 кг/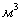, плотность водя 1000 кг/.

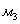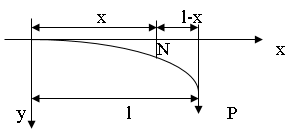
Изучаю тему «Дифференциальные уравнения» можно предложить следующие задачи: 1. Балка (с модулем упругости Е и моментом инерции J) наглухо заделана в конце О и подвергается действию сосредоточенной вертикальной силы Р, приложенной к концу балки L на расстоянии 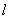 от места закрепления. Определить прогиб балки h на конце балки L.

2. Интенсивность тепловыделения бетона 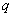 пропорциональна не выделившемуся к данному моменту времени количеству тепла: 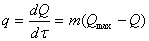, где 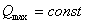 — максимальное количество тепла, которое может выделиться в бетоне данного состава при полной гидратации цемента,  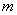— параметр, зависящий от типа цемента (для бетонов на портландцементе он изменяется в пределах от 0,010–0,015 1/ч). Определить функцию интенсивности тепловыделения бетона.

Литература:

1.        Гребенев И. В., Ермолаева Е. И., Круглова С. С. Математическая подготовка абитуриентов — основа получения профессионального образования в университете// Наука и школа, № 6, 2012г. С 27–31.

2.        Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов// Актуальные проблемы гуманитарных и естественных наук, № 7, 2010г. С. 270–272.

3.        Ермолаева Е. И. Математическое моделирование физических процессов в теории вероятностей// Актуальные проблемы гуманитарных и естественных наук. 2010. № 10. С. 13–15.

4.        Ермолаева Е. И., Куимова Е. И. О важности фундаментальной математической подготовки студентов по направлению «Строительство»// Известия Пензенского государственного педагогического университета им. В. Г. Белинского. 2011. № 26. С. 463–467.

5.        Крымская Ю. А., Титова Е. И., Ячинова С. Н. Профессиональная подготовка строителей через решение математических задач// Современные проблемы науки и образования, № 2, 2014.