Объект как система массового обслуживания: моделирование, исходные предпосылки и ограничения

Основным элементом, определяющим процессы в системе массового обслуживания, является входной поток. Нередко его можно рассматривать простейшим и стационарным пуассоновским потоком. В этом случае число k заявок в промежутке времени 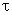 распределяется по закону Пуассона 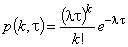;;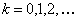  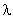— плотность (интенсивность потока), или среднее число событий в потоке за единицу времени,  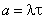— среднее число событий, приходящееся на интервал 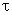. Физический смысл основных характеристик простейшего входного потока [1…3] проиллюстрируем на ряде примеров, имеющих и самостоятельный интерес.

Определим время 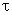 безотказной работы системы (режущий инструмент, покрышка колеса автомобиля и т. д.), а затем и поток отказов системы в этоминтервале. Если инструмент может получить повреждение с вероятностью 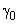, то вероятность того, что поломка инструмента произойдет при изготовлении k-го изделия (по теореме умножения вероятностей)

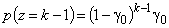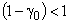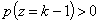,,                                                (1)

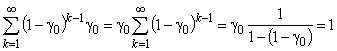;                                                  (2)

 формулой (1) задается геометрическое распределение дискретной случайной величины z (число изделий, изготовленных до поломки инструмента).

Если время изготовления одного изделия равно , то время безотказной работы инструмента 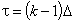. Вероятность изготовления более  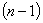изделия практически равна 0, то есть время безотказной работы инструмента практически не превышает .

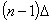Если 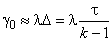,,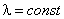 то 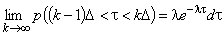. Если 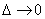, то дискретная случайная величина  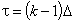фактически превращается в непрерывную. Напомним, если плотность распределения случайной величины есть 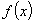, то 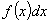 определяет вероятность попадания случайной величины в интервал 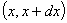. Так что

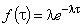                                                                                                                  (3)

 дает распределение вероятностей времени 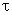 безотказной работы (показательное распределение).

Наконец, определим вероятность 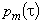 ровно m поломок в интервале времени при условиях: вероятность поломки инструмента в интервале времени при пренебрежимомало( 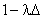— вероятность противоположного события); числа поломок на каждом изnнеперекрывающихся интервалов длиной являются независимыми. Непосредственно из формулы Бернулли следует, что вероятность ровно m поломок за время определится формулой

(поток поломок инструмента на интервале 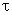 подчиняется закону Пуассона;

,,,; ).

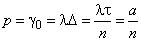Поток будет простейшим (стационарным пуассоновским; число событий попадающих на любой фиксированный интервал времени распределено по закону Пуассона), если он является:

-          стационарным (вероятность попадания того или иного числа событий на участок длиной зависит только от длины участка и не зависит от его расположения на оси 0t),

-          потоком без последействия (для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие),

-          ординарным (вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события).

Для простейшего потока среднее число событий в единицу времени равно ; .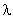

На практике часто встречается и поток Пальма (поток с ограниченным последействием). Например, если срок безотказной работы инструмента случаен (отдельные экземпляры инструмента выходят из строя независимо друг от друга; инструмент используется до поломки, после чего он заменяется на новый), то поток отказов (поток восстановления инструмента) дает поток Пальма. Если при этом срок работы детали распределен по показательному закону, то поток Пальма превращается в простейший.

При проектировании станций технического обслуживания автомобилей [4…7] нередко используется теорема Пальма о выходном потоке. А именно: если в систему массового обслуживания поступает поток заявок типа Пальма, и заявка при занятых каналах получает отказ (не обслуживается), то, если время обслуживания подчиняется показательному закону распределения, поток необслуженных заявок будет потоком Пальма (при простейшем входном потоке поток необслуженных заявок, не будучи простейшим, будет все же потоком Пальма). При показательном распределении длительности 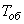 распределение длительности оставшейся части работы по обслуживанию не зависит от того, сколько оно продолжалось.

Если на станции имеется 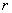 подъемников для обслуживания, то при  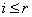требований (в момент 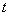)  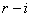подъемников остаются свободными; при  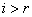обслуживаются  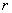требований,  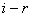остаются в очереди и ожидают обслуживания. Обозначим через  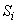состояние, когда в системе находится  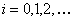требований, а через  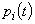— вероятность того, что система в моментtокажется в состоянии 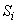. Если в момент t₀ система находится в состоянии 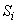, то дальнейшее течение обслуживания определяется:

-       моментами окончания обслуживаний, осуществляемых в момент t₀;

-       моментами появления новых требований,

-       длительностью обслуживания требований, поступивших после t₀.

Известно, длительность остающейся части обслуживания (в силу особенности показательного распределения) не зависит от времени обслуживания до момента времени t₀. При простейшем потоке требований прошлое не влияет на то, как много требований появится после t₀; длительность обслуживания требований, появившихся после t₀,не зависит от того, что и как обслуживалось до t₀. Как видим, в системе с ожиданием в случае простейшего потока и показательного времени обслуживания имеет место случайный процесс Маркова (процесс без последействия; будущее развитие зависит только от достигнутого в момент t₀ состояния 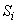 и не зависит от того, как происходило развитие в прошлом до моментаt₀).

Сразу после включения системы в работу возникает переходный нестационарный процесс. После затухания переходного процесса система перейдет на стационарный установившийся режим, вероятностные характеристики которого не будут зависеть от времени (существование таких решений определяется эргодическими теоремами). Стационарные вероятности определяются из уравнений:

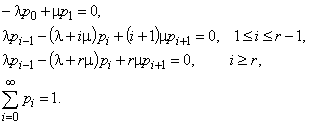
В частности, если на станции имеется три подъемника, рабочий день продолжается 8 часов, необходимость в подъемнике возникает четыре раза, среднее время обслуживания одной заявки 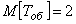 часа, то установившийся режим обслуживания существует (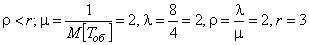):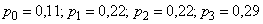; вероятность очереди 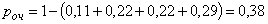; средняя длина очереди .

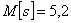Литература:

1.         Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.

2.         Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС. — 2011. — 308 с.

3.         Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. № 2(41). 2013. –С.123–130.

4.         Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. –№ 5. –С. 42–45.

5.         Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие. — Пенза: ПГУАС. — 2010. — 228 с.

6.         Гарькина И. А., Данилов А. М., ЛапшинЭ.В., Юрков Н. К. Системные методологии, идентификация систем и теория управления: промышленные и аэрокосмические приложения / Известия высших учебных заведений. Поволжский регион. Технические науки. — 2009. — № 1(9). — С.3–11.

7.         Гарькина И.А, Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин.–2013. –№ 1(40). –С.115–122.