Налаживание взаимовыгодных экономических связей, управление, анализ производственных процессов направлены, в первую очередь, на поиск наилучшего, оптимального, с точки зрения намеченной цели, варианта. Известно, что наиболее разработанными, хорошо адаптированными и распространенными являются математические модели, реализуемые с помощью методов линейного программирования. Линейное программирование изучает задачи оптимизации, в которых целевая функция является линейной функцией независимых переменных, допустимые значения которых определяются из условий, имеющих вид линейных уравнений и неравенств.
Основным, универсальным методом решения задач линейного программирования является симплексный метод. Однако, многие классы широко распространенных на практике задач приводят к задачам линейного программирования, которые можно решать более простыми методами. Наиболее широким классом таких задач являются задачи распределительного типа, позволяющие существенно упростить расчеты, повысить точность вычислений и снизить затраты времени на ввод исходной информации.
Первоначально распределительный метод применялся в задачах, связанных с транспортировкой грузов, их распределением между несколькими пунктами отправления и приема, вследствие чего и получил название «транспортная задача».
В настоящее время транспортная задача получила широкое применение, в том числе и в системах военного назначения: материально-технического обеспечения операций; целераспределения; организации ремонта и восстановления военной техники 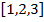 .
.
Математически транспортная задача формулируется следующим образом. Требуется минимизировать:
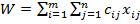 (1)
(1)
при ограничениях
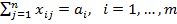 (2)
(2)
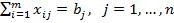 (3)
(3)
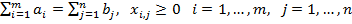 (4)
(4)
где
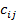 — стоимость перевозки единицы груза из i-го пункта отправления до j-го пункта назначения;
— стоимость перевозки единицы груза из i-го пункта отправления до j-го пункта назначения;
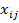 –количество груза, перевезенного i-го пункта отправления в j-й пункт назначения;
–количество груза, перевезенного i-го пункта отправления в j-й пункт назначения;
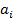 — запасы груза на i-м пункте отправления;
— запасы груза на i-м пункте отправления;
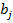 — потребности в грузе на j-м пункте назначения.
— потребности в грузе на j-м пункте назначения.
Условия (2) и (3) означают, что количество груза, вывозимого из i-го пункта отправления, равно запасам груза в этом пункте, и количество груза, ввозимого в j-й пункт назначения, равно потребностям в грузе для данного пункта назначения. Из условия (4) следует, что общие запасы потребности в грузе равны.
Показателем эффективности плана перевозок является стоимость, поэтому сформулированную задачу называют транспортной задачей по критерию стоимости. Величина 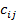 может иметь не только стоимостный смысл. Например,
может иметь не только стоимостный смысл. Например, 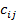 может означать расстояние, время, расход топлива и т. п.
может означать расстояние, время, расход топлива и т. п.
Одним из методов решения транспортной задачи является венгерский метод. Вычислительный алгоритм метода следующий:
1. Преобразуем исходную матрицу 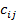 таким образом, чтобы в каждом столбце и каждой строке был хотя бы один нулевой элемент. Для этого вычитаем минимальные элементы столбцов из всех элементов соответствующих столбцов с последующим вычитанием минимальных элементов строк из всех элементов соответствующих строк.
таким образом, чтобы в каждом столбце и каждой строке был хотя бы один нулевой элемент. Для этого вычитаем минимальные элементы столбцов из всех элементов соответствующих столбцов с последующим вычитанием минимальных элементов строк из всех элементов соответствующих строк.
2. Определим начальный опорный план 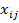 , назначая перевозки способом «северо-западного угла» в нулевые элементы
, назначая перевозки способом «северо-западного угла» в нулевые элементы 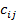 .
.
3. Определим невязки по строкам 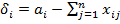 и столбцам
и столбцам 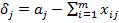 и суммарную невязку
и суммарную невязку 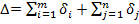 . Если
. Если 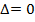 , то план является допустимым и оптимальным. Если
, то план является допустимым и оптимальным. Если 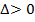 , то план недопустимый и дальнейшая вычислительная процедура направлена на ликвидацию невязок.
, то план недопустимый и дальнейшая вычислительная процедура направлена на ликвидацию невязок.
4. Выделим столбцы 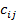 , для которых
, для которых 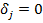
5. Находим среди невыделенных элементов 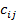 минимальный элемент h. При
минимальный элемент h. При 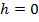 переходим к п.7, при
переходим к п.7, при 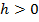 — к п.6.
— к п.6.
6. Вычитаем h из всех элементов невыделенных строк 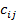 и прибавляем h ко всем элементам выделенных столбцов. Возвращаемся к п. 5.
и прибавляем h ко всем элементам выделенных столбцов. Возвращаемся к п. 5.
7. Отметим нулевой элемент h матрицы 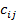 знаком «штрих» (0').
знаком «штрих» (0').
8. Проверяем невязку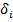 строки, в которой находится 0'. При
строки, в которой находится 0'. При 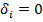 переходим к п. 9, при
переходим к п. 9, при 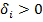 — к п. 13.
— к п. 13.
9. Выделим в 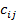 строку, в которой находится 0'.
строку, в которой находится 0'.
10. В выделенной строке по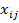 последовательно проверяем в выделенных столбцах значения
последовательно проверяем в выделенных столбцах значения 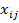 . При
. При 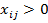 переходим к п. 12.
переходим к п. 12.
11. Открываем в 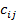 выделенный столбец и отмечаем нулевой элемент этого столбца, находящийся в выделенной строке, звездочкой (0*).
выделенный столбец и отмечаем нулевой элемент этого столбца, находящийся в выделенной строке, звездочкой (0*).
12. Если проверены все выделенные столбцы 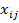 , переходим к п. 5, в противном случае — к п. 10.
, переходим к п. 5, в противном случае — к п. 10.
13. Строим цепочку по столбцу от 0' к 0*, по строке от 0* к 0'. Цепочка начинается от 0', находящегося в столбце с 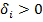 , и заканчивается в 0', находящемся в столбце с
, и заканчивается в 0', находящемся в столбце с 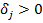 . Возможен случай, когда цепочка содержит только один 0', т. е.0' находится в строке и столбце, для которых
. Возможен случай, когда цепочка содержит только один 0', т. е.0' находится в строке и столбце, для которых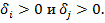
14. Определяем величину сокращения невязки: 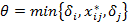 , где
, где 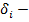 невязка строки, в которой находится первый 0' цепочки;
невязка строки, в которой находится первый 0' цепочки;  0' цепочки,
0' цепочки, 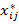 - минимальное значение перевозок, соответствующее 0*, входящему в цепочку. Если в цепочку входит один 0', то
- минимальное значение перевозок, соответствующее 0*, входящему в цепочку. Если в цепочку входит один 0', то 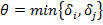 .
.
15. Находим новый план, прибавляя 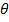 к элементам
к элементам 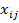 , соответствующим 0' цепочки, и вычитая
, соответствующим 0' цепочки, и вычитая 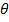 из элементов
из элементов 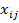 , соответствующим 0* цепочки. Остальные элемент остаются без изменений.
, соответствующим 0* цепочки. Остальные элемент остаются без изменений.
16. Раскрываем все выделенные столбцы и строки, стираем у нулевых элементов знаки штриха и звездочки переходим к п. 3.
Представленный алгоритм наглядно показывает, что венгерский метод формализован, но достаточно сложен. Поэтому его удобно реализовывать на компьютере. На кафедре автоматизированных систем управления и программного обеспечения Пензенского артиллерийского инженерного института разработана и внедрена программа для решения транспортной задачи венгерским методом 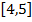 .
.
Пример. Определить оптимальный (по минимуму суммарного расхода горючего) план доставки боеприпасов с артиллерийских складов в подразделения, если наличие и потребности боеприпасов, а также расход горючего на доставку одного БК с каждого склада в каждое подразделение заданы таблицей следующего вида:
|
B1 |
B2 |
B3 |
аi | |
|
A1 |
10 |
1 |
3 |
40 |
|
A2 |
6 |
2 |
2 |
80 |
|
A3 |
12 |
5 |
14 |
60 |
|
bj |
30 |
100 |
50 |
Решение задачи с помощью разработанного программного обеспечения представлено на рисунке 1.
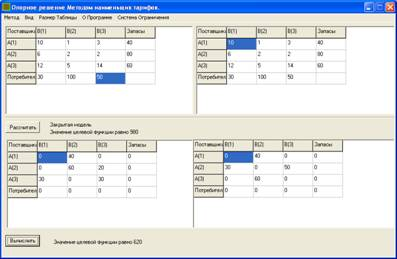
Рис. 1. Решение транспортной задачи венгерским методом
Вычислительные эксперименты показали эффективность разработанного программного обеспечения, реализующего венгерский метод решения военно-прикладных задач, и в частности, транспортной задачи.
Литература:
1. Культин П. Б. Самоучитель С++Builder — СПб.: БХВ-Петербург, 2004–320 с.
2. Бочкарева, О. В. Математические задачи как средство формирования профессиональных качеств личности / О. В. Бочкарева, Т. Ю. Новичкова, О. В. Снежкина, Р. А. Ладин // Современные проблемы науки и образования. — 2014. — № 2;
3. URL: www.science-education.ru/116–12584
4. Бочкарева, О. В. Формирование профессиональных умений на занятиях по математике / О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый — 2014. -№ 2(61). –С. 735–738.
5. Привалов А. Н. Методы оптимизации в системах военного назначения. Часть 2. Из-во ТАИИ, 2006 г — 86 с.
6. Бочкарева, О. В. О роли профессионально ориентированных задач в обучении математике / О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый — 2014. № 3(62). — С.877–879.

