Рассматриваются проблемы стабилизации орбитального движения космического аппарата в окрестности коллинеарной точки либрации системы Солнце–Земля. Для управляемой системы уравнений движения космического аппарата анализируется связь между поведением специальной функции фазовых переменных, называемой в работе «функцией опасности», и областью управляемости. Проводится численный анализ управляемых траекторий с законами управления, которые демпфируют «функцию опасности» и обеспечивающими пребывание космического аппарата в окрестности точек либрации L1, L2системы Солнце–Земля в течение длительного времени. Результаты численного моделирования проиллюстрированы графически.
Ключевые слова: круговая ограниченная задача трех тел, задача Хилла, коллинеарная точка либрации, управляемое орбитальное движение, область управляемости.
Введение. Известно, что некоторые математические модели, такие как задача двух тел и задача трех тел, являются полезными для разработки проектов, связанных с исследованием космического пространства. Одной из наиболее известных моделей движения является модель ограниченной круговой задачи трех тел [1].
Уравнения движения космического аппарата (КА), получаемые в рамках ограниченной задачи трех тел Солнце–Земля–КА, как показали Эйлер и Лагранж [2], имеют частные решения, сохраняющие положение в пространстве конфигураций, они и получили название либрационных.
С использованием теоретических свойств точек либрации связаны многие проекты, как освоения космического пространства, мониторинга околоземного космического пространства, так и защиты Земли от потенциально опасных космических объектов.
Уравнения движения и их характеристика. Пусть КА движется в окрестности коллинеарных точек либрации L1 или L2. Тогда в рамках хилловского приближения круговой ограниченной задачи трех тел Солнце–Земля–КА уравнения управляемого движения КА во вращающейся системе координат имеют вид [3–6]:
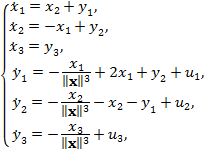 (1)
(1)
где центр инерции Земли совпадает с началом системы координат, а ось 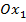 направлена вдоль оси, соединяющей центры масс Земли и Солнца. Здесь
направлена вдоль оси, соединяющей центры масс Земли и Солнца. Здесь 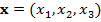 — вектор координат КА,
— вектор координат КА, 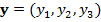 — вектор импульсов,
— вектор импульсов, 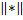 — евклидова норма. Точки либрации L1 и L2 во вращающейся системе неподвижны и имеют координаты
— евклидова норма. Точки либрации L1 и L2 во вращающейся системе неподвижны и имеют координаты 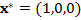 ,
, 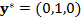 и
и 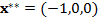 ,
, 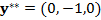 , соответственно. За единицу расстояния принята величина, равная
, соответственно. За единицу расстояния принята величина, равная 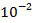 а. е., за единицу времени —
а. е., за единицу времени — 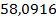 суток (год, деленный на
суток (год, деленный на 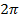 ).
).
На значение управляющих воздействий 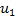 ,
, 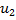 ,
, 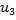 имеются ограничения
имеются ограничения
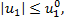
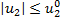 ,
, 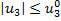 .
.
Неуправляемая система (1) является гамильтоновой, где функция Гамильтона 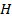 представляется в виде
представляется в виде
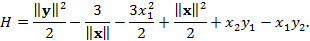
Система линеаризованных уравнений в окрестности коллинеарных точек либрации L1 или L2 имеет вид
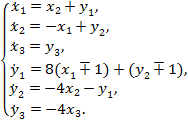 (2)
(2)
Замечание. Выбор знака в выражении для 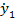 соответственно зависит от рассматриваемой окрестности коллинеарной точки либрации L1 или L2.
соответственно зависит от рассматриваемой окрестности коллинеарной точки либрации L1 или L2.
Матрица линеаризованной системы (2) имеет набор собственных значений [4]
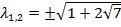 ,
, 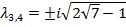 ,
, 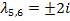 .
.
Замечание. Из положительности собственного значения 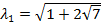 следует неустойчивость точки либрации L1 и L2.
следует неустойчивость точки либрации L1 и L2.
Так как последние два уравнения, соответствующие пространственным переменным (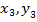 ), отделяются от остальных, удобно рассмотреть задачу нахождения законов управления отдельно для системы плоского движения:
), отделяются от остальных, удобно рассмотреть задачу нахождения законов управления отдельно для системы плоского движения:
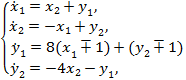 (3)
(3)
и системы пространственных переменных:
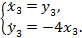 (4)
(4)
Замечание. Для неуправляемой системы (4) (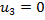 ) в силу интеграла энергии имеет место устойчивость по Ляпунову стационарного решения.
) в силу интеграла энергии имеет место устойчивость по Ляпунову стационарного решения.
Из проведенного анализа системы уравнений орбитального движения КА можно сделать вывод, что неустойчивость коллинеарной точки либрации, с одной стороны, требует стабилизирующего управления, а с другой стороны, может быть использована как положительный фактор в задачах маневрирования [7, 8].
Функция опасности, область управляемости. Выше было показано, что стационарное решение уравнений неуправляемого движения, соответствующее коллинеарной точке либрации, является неустойчивым положением равновесия. Поэтому весьма актуальной будет задача стабилизации КА в окрестности точки либрации.
В связи с этим возникает вопрос: поскольку на практике управляющее воздействие ограничено, то какова будет область управляемости, т. е. область, в которой возможно удержание КА при ограничениях на управления.
Пусть 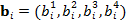 — собственный вектор, соответствующий собственному значению
— собственный вектор, соответствующий собственному значению 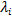 линеаризованной управляемой системы (3), а
линеаризованной управляемой системы (3), а 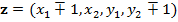 .
.
Определим линейные формы 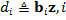 =1,…,4, тогда в силу неуправляемой системы (3) справедливы равенства
=1,…,4, тогда в силу неуправляемой системы (3) справедливы равенства
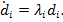 (5)
(5)
Если в (5) положить 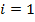 , то
, то
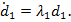 (6)
(6)
Дифференциальное уравнение (6) имеет решение
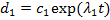 ,(7)
,(7)
где 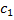 – некоторая постоянная интегрирования.
– некоторая постоянная интегрирования.
Легко видеть, что решение 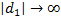 при
при 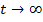 , когда
, когда 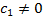 .
.
Отсюда следует, что определенная функция 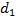 экспоненциально возрастает (когда
экспоненциально возрастает (когда 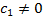 ) и ее рост определяется равенством (7).
) и ее рост определяется равенством (7).
Если же 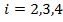 , то
, то
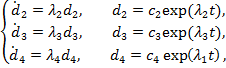
где 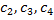 – некоторые постоянные интегрирования.
– некоторые постоянные интегрирования.
Функция 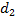 экспоненциально стремится к нулю, когда
экспоненциально стремится к нулю, когда 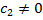 . Функции
. Функции 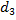 и
и 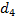 описывают колебательный процесс.
описывают колебательный процесс.
Линейная форма 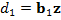 играет важную роль в задаче стабилизации и называется функцией опасности [9, 10].
играет важную роль в задаче стабилизации и называется функцией опасности [9, 10].
Тогда, если нам удастся некоторым образом обеспечить выполнение условия ограниченности функции 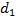 в окрестности коллинеарной точки либрации, т. е. выполнение неравенства
в окрестности коллинеарной точки либрации, т. е. выполнение неравенства
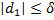 , (8)
, (8)
где 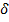 — достаточно малая величина, то КА будет находиться в некоторой окрестности коллинеарной точки либрации достаточно длительное время (быстрого ухода по экспоненте, по крайней мере, в линейном приближении не будет).
— достаточно малая величина, то КА будет находиться в некоторой окрестности коллинеарной точки либрации достаточно длительное время (быстрого ухода по экспоненте, по крайней мере, в линейном приближении не будет).
В случае управляемого движения КА для производной функции 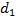 можем записать (в силу линеаризованной системы уравнений движения (3))
можем записать (в силу линеаризованной системы уравнений движения (3))
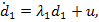
где 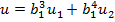 .
.
Откуда для обеспечения ограничения функции опасности в линейном приближении необходимо и достаточно, чтобы
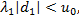 (9)
(9)
где 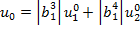 .
.
Смысл данного неравенства заключается в том, что по значению величины 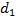 можно судить о возможности стабилизации КА в окрестности коллинеарной точки либрации, поскольку при нарушении неравенства (9) (слишком большое значение функции опасности) стабилизация станет невозможной.
можно судить о возможности стабилизации КА в окрестности коллинеарной точки либрации, поскольку при нарушении неравенства (9) (слишком большое значение функции опасности) стабилизация станет невозможной.
Проведенное исследование дает математическую базу для построения (с помощью функции опасности) не только алгоритмов стабилизации движения КА, но, например, и поиска траекторий возвращения КА в окрестность точки либрации [7].
Управления, стабилизирующие орбитальное движение КА. Предположим, что с помощью управляющего воздействия удалось добиться ограничения по модулю функции опасности (8).
Возникает вопрос: достаточно ли выполнения условия (8) для того, чтобы КА оставался в окрестности коллинеарной точки либрации. Этот вопрос в теоретическом плане представляет собой качественное исследование нелинейной системы (1) с соответствующими управлениями.
В этой работе представим результаты численного исследования, поведения траекторий движения КА с управлениями, обеспечивающими ограничение (8).
Примером таких управлений могут быть управления с компонентами [10]:
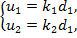 при
при 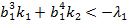 , (10)
, (10)
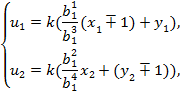
при 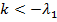 , (11)
, (11)
где 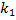 ,
, 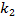 и
и 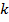 — вещественные константы, удовлетворяющие неравенствам в (10) и (11).
— вещественные константы, удовлетворяющие неравенствам в (10) и (11).
Численные эксперименты. Приведем несколько примеров с предложенными законами управления. Проинтегрируем нелинейную систему (1) на промежутке времени, соответствующему 50 единицам (около 8 лет), с начальными данными:
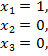
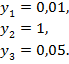
Выбор таких начальных данных связан с предположением, что КА, находясь в фазовом пространстве с координатами точки L1, получил дополнительный импульс вдоль составляющих 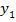 и
и 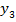 вектора
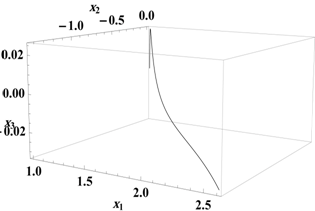
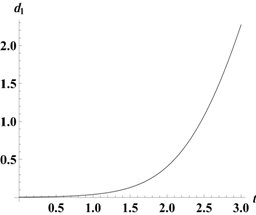
вектора 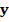 . На рис. 1 представлена траектория неуправляемого движения КА на промежутке времени
. На рис. 1 представлена траектория неуправляемого движения КА на промежутке времени 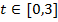 , за которое наблюдается уход на расстояние порядка
, за которое наблюдается уход на расстояние порядка 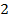 млн. км.
млн. км.
|
|
|
|
Рис 1. Траектория КА без управления (слева) и соответствующий ей график значения функции опасности (справа) | |
|
|
|
|
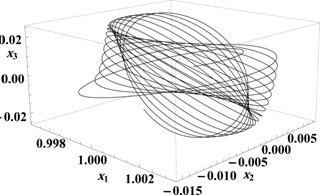
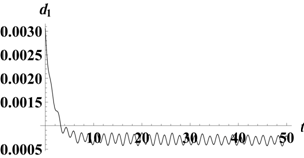
Рис 2. Траектория движения КА с управлением (10) при | |
|
|
|
|
Рис 3. Траектория движения КА с управлением (11) при | |
Заключение. Таким образом, была показана возможность стабилизации КА в окрестности коллинеарной точки либрации с помощью управляющего воздействия, которое демпфирует функцию опасности.
Необходимо отметить возможность осуществления такого рода управлений на практике, например, в случае использования таких технических систем управления как солнечный парус. Его применение становится возможным в силу того, что управляющие ускорения оказываются достаточно малыми по величине (порядка 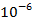 м/c2).
м/c2).
Литература:
1. Брюно А. Д. Ограниченная задача трех тел. М.: Наука, 1990. 295 с.
2. Маркеев А. П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978. 312 с.
3. Hill G. W. Researches in the lunar theory // Amer. Journal of Mathematics, 1878. Vol. 1. P. 5–26, 129–147, 245–260.
4. Шмыров В. А. Стабилизация управляемого орбитального движения космического аппарата в окрестности коллинеарной точки либрации L1 // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2005. Вып. 2. С. 193–199.
5. Shmyrov A., Shmyrov V. Controllable orbital motion in a neighborhood of collinear libration point // Applied Mathematical Sciences, 2014. Vol. 8, № 10. P. 487–492.
6. Шмыров А. С., Шмыров В. А. Синтез оптимального управления орбитальным движением в окрестности коллинеарной точки либрации // Вестн. С.-Петерб. ун-та. Сер. 1: Математика, механика, астрономия, 2012. Вып. 4. С. 139–146.
7. Шиманчук Д. В., Шмыров А. С., Построение траектории возвращения в окрестность коллинеарной точки либрации системы Солнце—Земля // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2013. Вып. 2. С. 76–85.
8. Kulakov F., Shmyrov A., Shymanchuk D. Supervisory Remote Control of Space Robot in an Unstable Libration Point // Proceedings — 7th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing System: Technology and Applications 12–14 September 2013, Berlin, Germany. Berlin, 2013. Vol. 2. P. 925–928
9. Шмыров А. С., Шмыров В. А. Об асимптотической устойчивости по отношению к части переменных орбитального движения космического аппарата в окрестности коллинеарной точки либрации // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2009. Вып. 4. 250–257.
10. Шиманчук Д. В. Моделирование орбитального управляемого движения космического аппарата в окрестности коллинеарной точки либрации L1 // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2010. Вып. 3. С. 86–92.
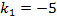 ,
, 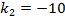 (слева) и соответствующий ей график значения функции опасности (справа)
(слева) и соответствующий ей график значения функции опасности (справа)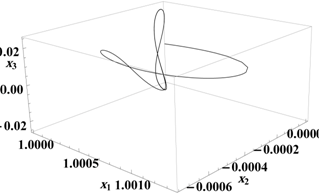

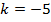 (слева) и соответствующий ей график значения функции опасности (справа)
(слева) и соответствующий ей график значения функции опасности (справа)
