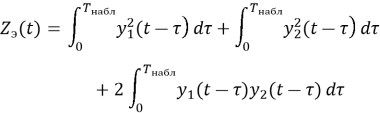Актуальность работы
Исследование радиолокационных станций и систем методами математического моделирования предполагает получение оценок параметров и характеристик статистической обработки входных данных. При этом, в силу временных ограничений на проведение моделирования, объем этих данных также ограничен. В связи с этим, исследователь должен оценивать качество результатов обработки применяя специальные методы, дающие приемлемый результат в указанных условиях.
Для радиолокационных станций обнаружения целей и измерения их координат вне зависимости от вида радиолокации (активной или пассивной), применяемой для получения данных, наибольшую значимость имеют показатели качества обнаружения, которые в соответствие с критерием Неймана-Пирсона характеризуются условной вероятностью правильного обнаружения при фиксированной условной вероятности ложной тревоги. Оценки этих показателей качества получаются при заданном пороге обнаружения, значение которого определяется уровнем собственного шума приемного тракта, плотностью его распределения и значением заданной условной вероятности ложной тревоги. Таким образом, в процессе математического моделирования процесса обработки сигналов и получения оценок показателей качества обнаружения РЛС требуется знание плотности распределения шума и величины порога обнаружения.
В данной статье авторы, на основе личного опыта проведения исследований в области радиопеленгации, представляют методику расчета порога обнаружения при ограниченном объеме входных данных с использованием аппарата проверки статистических гипотез о законах распределения случайных величин по минимальному набору входных данных.
Постановка задачи
В ходе оценки показателей качества обнаружения сигналов от источников радиоизлучения макетом пассивного двухканального обнаружителя-пеленгатора требуется вычисление порога обнаружения
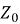
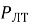
Исходные данные
Входные реализации шума приемного тракта представляют из себя независимые стационарные случайные процессы
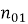
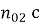
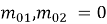
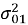
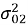
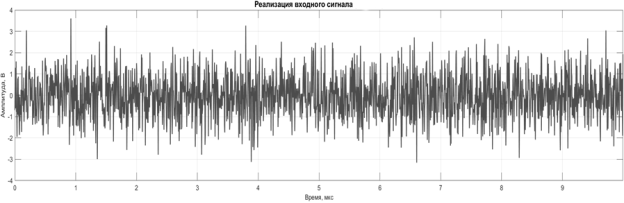
Рис. 1. Реализация входного шума
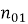
Для статистического моделирования собственного шума было использовано выражение числового вектора
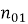
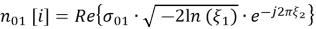
где
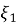
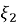
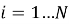
В качестве достаточной статистики обнаружения использовался результат совместной обработки сигналов от двух приемных каналов, реализующих классический амплитудный метод пеленгации по критерию максимума отношения правдоподобия при условии распределения шума по нормальному закону. Аналитический вид достаточной статистики представлен формулой (2).
|
|
(2) |
Анализ выражения показывает, что в процессе обработки входные реализации сигналов возводятся в квадрат, что приводит к изменению их статистических характеристик. При наличии во входной реализации только шума плотность распределения выходной статистики будет подчиняться закону Рэлея. Это приводит к снижению отношения сигнал-шум на выходе устройства обработки и зависимости порогового значения от времени интегрирования (накопления). Таким образом, при исследовании данного способа обработки требуются знания о законе распределения шума на выходе и получении оценок его параметров для пересчета порогов обнаружения.
Описание методики расчета порога обнаружения
- Определение закона распределения выходной статистики
Для определения закона распределения реализуется статистический эксперимент, при котором многократно вычисляется достаточная статистика (2) при подаче на вход реализаций шума (1). Полученные значения статистики используются для построения вариационного ряда, который записывается в виде таблицы частот в пределах между минимальным и максимальным экстремальными значениями с разбиением на заданные интервалы [1, c. 136]. Графически вариационный ряд можно представить в виде полигона частот (гистограммы), т. е. количества попаданий значений статистики в заданные интервалы, отнесенных к объему выборки.
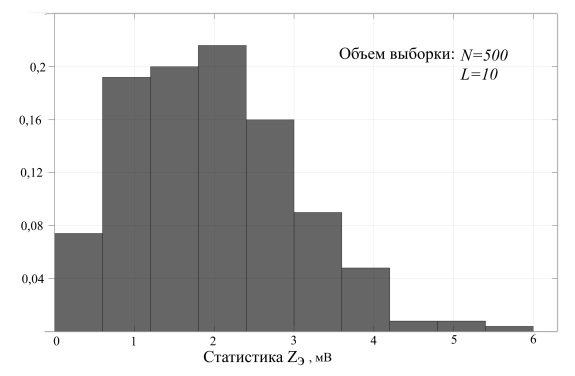
Рис. 2. Полигон частот выборки значений достаточной статистики
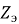
По виду полигона частот делается предположение о виде распределения достаточной статистики. В рассматриваемом случае статистики (2) предполагается, что она распределена по закону Рэлея:
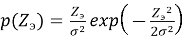
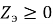
где
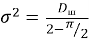
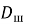
На основании этого реализуется проверка статистической гипотезы по критерию согласия
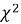
Статистика критерия вычисляется по формуле:
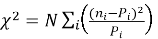
где
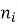
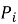
Теоретическая вероятность попадания случайной величины
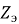
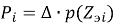
где
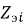
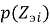
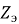
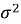
Очевидно, что чем меньше разница между
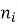
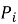
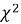
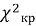
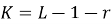
где L — количество интервалов разбиения;
r — количество параметров предполагаемого распределения.
Для выбранного закона распределения Рэлея r=1, при L=10,
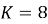
Критическое значение
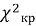
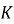
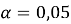
Текущее значение
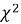
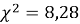
Таким образом,
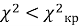
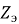
Эмпирическая и теоретическая плотности распределения статистики
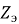
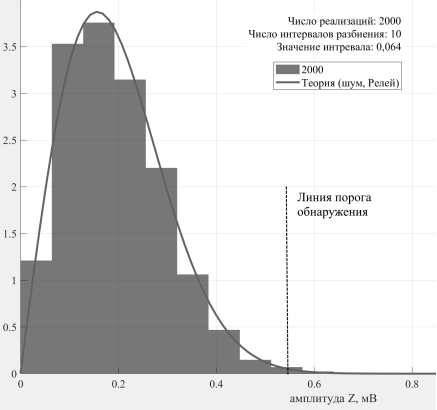
Рис. 3. Эмпирическая и теоретическая плотности распределения статистики
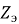
- Расчет порога обнаружения
В соответствие с известным критерием Немана-Пирсона [2, c. 84] качество обнаружения оценивается по величине условной вероятности правильного обнаружения
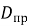
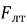
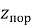
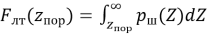
В рассматриваемом случае
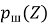
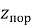
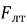
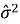
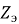
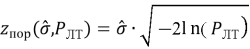
Следует отметить, что значения
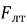
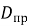
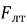
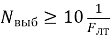
Выводы
Таким образом, расчет порога принятия решения для оценки показателей качества обнаружения может производиться по изложенной выше методике на основании выборки достаточной статистики ограниченной размерности, с использованием методов проверки статистических гипотез при заданном значении условной вероятности ложной тревоги и полученной оценки параметра закона распределения. Данная методика применима для любых законов распределения и с успехом применяется авторами в процессе своей научной работы в области радиолокации и радиопеленгации.
Литература:
- Вентцель, Е. С. Теория вероятности / Е. С. Вентцель. — М.: Наука, 1969. — 576 с. — Текст: непосредственный.
- Теоретические основы радиолокации / Под ред. Ширмана Я. Д. Учебное пособие для вузов — М.: Советское радио, 1970. — 560 с. — Текст: непосредственный.