Введение
Математическое описание характеристик сетевого трафика необходимо при разработке архитектур многомашинных вычислительных систем (МВС), а также соответствующих им алгоритмов анализа и балансировки потоков данных возникающего сетевого трафика. Сложность архитектур современных МВС, содержащих большое число взаимодействующих узлов (серверов, мэйнфреймов, коммуникационных пулов и т. п.), обуславливает не только значительную интенсивность сетевых транзакций, но также сильную вариативность межпакетных интервалов и, следовательно, изменение характера трафика. В результате алгоритмы обработки и балансировки потоков данных, основанные либо на предположении о стационарности и симметрии распределения транзакций, либо ориентированные на определенные типы приложений, оказываются неэффективными в условиях пульсирующего и изменяющегося характера сетевого трафика. Таким образом, возникает необходимость в создании математических моделей сетевого трафика МВС, учитывающих различные формы, асимметрию, эксцесс, «тяжелые хвосты» его распределений [1–3].
Действительно, например, модель Пуассона [4] фактически определяет МВС как систему массового обслуживания, где транзакции формируют поток пакетов (заявок), интервал поступления между которыми подчиняется экспоненциальному закону распределения с известной (заданной) интенсивностью. Логическим продолжением такого подхода можно считать модель On/Off [5], когда выделяются активное и пассивное состояния источника трафика. Такая модель представляет собой одноканальную систему массового обслуживания с двумя состояниями, причем вероятности переходов из активного состояния в пассивное состояние и наоборот также подчиняются экспоненциальному закону распределения с известными интенсивностями. Очевидно, такие модели не могут отразить пульсации трафика, хотя находят свое применение в видеотелефонии при условии стационарности процессов в МВС.
Известны работы [4–6], в которых предлагаются различные стохастические модели, описывающие специфические виды поведения сетевого трафика. Например, авторегрессионная (autoregressive — AR) модель n -го порядка AR( n ) представляет трафик как статистическую линейную модель временного ряда, при которой текущее значение числа транзакций зависит от n предыдущих значений и случайного отклонения (ошибки). Модель AR подходит для относительно «спокойного» трафика (например, телетрафика с видеоданными), когда наблюдается сильная корреляция между пакетами в n моментах времени. Добавление к модели AR модели скользящего среднего (Moving Average — MA) для сглаживания отклонений определяет модель с авторегрессионным скользящим средним ARMA (autoregressive moving average). Поскольку трафик в МВС может в ряде случаев иметь сезонный характер, то модель ARMA может успешно использоваться для прогнозирования такого трафика (например, BitTorrent [7]), а также для несанкционированных вторжений и атак [8]. Другая популярная модель с авторегрессионным интегрированным скользящим средним ARIMA (autoregressive integrated moving average) сегодня широко используется для прогнозирования трафика, оценки производительности МВС, а также аномального поведения трафика (например, DDoS-атаки) [4–6].
Модели на основе цепей Маркова, особенно т. н. «скрытые» Марковские модели, могут использоваться для формирования различных типов трафика с поддержкой различных протоколов (HTTP, FTP, SMTP, SSH, Gnutella, BitTorrent и eDonkey). Наиболее известной моделью из данного класса моделей является пуассоновский процесс с Марковской модуляцией его интенсивности (Markov Modulated Poisson Process — MMPP), то есть представляет собой результат агрегирования нескольких пуассоновских потоков с одинаковой интенсивностью, где активные состояния определяются схемой «гибели-размножения». Поскольку условие стационарности пуассоновских потоков данных в МВС не выполняется, то модель ММРР инициализируется набором оценок параметров, которые являются случайными величинами, что влияет на качество верификации и параметризации сетевого трафика.
В ряде работ (например, [8]) было показано, что пакеты, которые формально передаются независимо, при их перемещении в компьютерных сетях, в том числе и в МВС, формируют потоки, представляющие самоподобные процессы, степень самоподобия которых оценивается с помощью параметра Херста. Cамоподобные процессы характеризуются распределениями с «тяжелыми хвостами» и медленно убывающей автокорреляционной функцией. Такие распределения достаточно хорошо описываются моделями Парето и Вейбулла. Моделирование самоподобных процессов возможно также с помощью вышерассмотренных моделей временных рядов AR, ARMA, ARIMA. Для моделирования самоподобного трафика отдельно выделяют класс фрактальных моделей, к которому относят фрактальное броуновское движение, фрактальный гауссовский шум, фрактальную модель ARIMA, фрактальный On/Off процесс и фрактальный процесс восстановления. Фрактальные модели трафика можно использовать для анализа явления его пульсации (Burstiness), а также для обнаружения DDoS-атак или перегрузок в МВС. К сожалению, количество используемых пакетов, необходимое для функционирования фрактальной модели в реальном масштабе времени, ограничено, что приводит к неправильным решениям относительно характера поведения трафика и ошибкам прогнозирования.
Отдельно следует отметить использование нейронных сетей, в частности, рекуррентных нейронных сетей (recurrent neural network), которые теоретически могут обнаруживать аномальное поведение, например, резкое увеличение числа транзакций в МВС, вызванное атакой, идентифицировать типы атак, а также моделировать сложные комбинации различных событий в МВС. К сожалению, только применение многослойных нейронных сетей позволит успешно решить задачу моделирования сетевого трафика, что, в свою очередь, сталкивается с необходимостью иметь полные и репрезентативные датасеты для обучения и забирать относительно много вычислительных ресурсов [2].
Таким образом, из вышеприведенного краткого обзора следует, что каждая из рассмотренных моделей может быть применима в строго определенных условиях, при этом для ее адекватной работы требуется предварительная настройка параметров, отражающих интенсивность, длительность активных состояний, вероятности переходов и другие особенности конкретного сетевого трафика. В результате с практической точки зрения возникает задача разработки универсального метода моделирования сетевого трафика, который допускает воспроизведение различных видов поведения трафика в рамках одного алгоритмического решения.
Предлагаемый в статье метод использует систему распределений Пирсона, которая до недавнего времени применялась в сетевых технологиях лишь фрагментарно — в основном для описания временных характеристик, таких как задержки или интервалы поступления пакетов [9]. При этом в большинстве случаев выбор конкретного типа распределения выполнялся вручную или на основе ограниченного набора статистических признаков. Описываемый ниже метод имитационного моделирования определяет тип распределения по оценкам статистических параметров наблюдаемого сетевого трафика, что позволяет автоматически идентифицировать и имитировать сетевой трафик в реальном масштабе времени.
Постановка задачи
Распределениями Пирсона называются непрерывные распределения, плотности вероятности которых являются решениями дифференциального уравнения [9]:
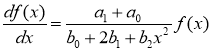
где
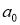
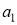
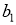
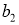
Пусть
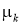
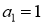
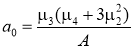
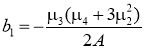
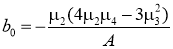
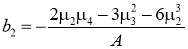
где
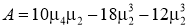
В соответствии с распределением корней квадратного трехчлена
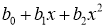
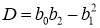
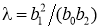
Пусть
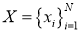
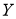
Этап верификации и параметризации
С точки зрения процесса обучения, этап верификации и параметризации включает следующие шаги.
- Вычисление второго, третьего и четвертого центральных моментов:
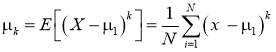
где
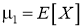
-
Подстановка в выражения для коэффициентов
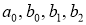
-
Оценка параметра
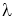
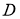
-
Идентификация типа распределения на основании таблицы классификации, составленной по знаку и значениям параметра
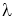
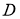
Этап имитации
На этапе имитации необходимо использовать датчики случайных чисел (ДСЧ), которые генерируют последовательности псевдослучайных чисел по определенному выше закону распределения. Как известно, распределения Пирсона включают «классические» распределения (тип I — бета-распределение, тип III — гамма-распределения, тип VII — распределение Стьюдента, тип X — показательное распределение, тип XI — нормальное распределение), для которых уже созданы алгоритмические и соответствующие программные решения, реализованные в различных средах моделирования (например, Matlab) и библиотеках (например, Python). Другие типы распределений требуют моделирования специализированных ДСЧ, параметры которых (в частности, длина и количество интервалов разбиения гистограмм) будут варьироваться в зависимости от вычисленных параметров функций плотности вероятности.
Оценка эффективности предложенного метода
Для оценки эффективности предложенного метода был проведен сравнительный анализ последовательностей транзакций, сформированных с использованием различных моделей сетевого трафика МВС. В качестве объектов моделирования выбраны: реальные данные конкретной МВС, авторегрессионная модель (AR), Марковский модулированный пуассоновский процесс (MMPP), модель ON–OFF, псевдогенератор MirageNet, генеративная модель PACGAN и итеративная модель NetDiffusion. Объем каждой выборки составил 256 элементов. Для получения устойчивых статистик выполнена серия из 500 экспериментов.
Имитационное моделирование проводилось в среде MATLAB, где используется встроенная функция
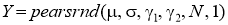
осуществляющая непосредственную генерацию псевдослучайных чисел, распределенных по закону из семейства распределений Пирсона по указанным параметрам, здесь
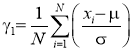
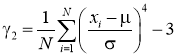
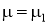
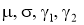
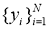
Для оценки степени соответствия результирующей последовательности исходной выполнялось сравнение оценок статистических характеристик, построение гистограмм и временных диаграмм сигналов и вычисление относительных погрешностей:
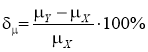
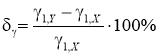
Результаты имитационного моделирования представлены в таблице 1.
Таблица 1
Статистические характеристики и типы распределений Пирсона
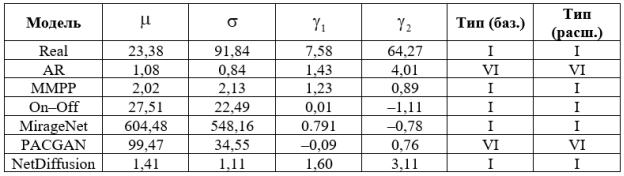
Анализ показал, что большинство источников трафика описываются распределениями типа I, что соответствует сильно асимметричным законам распределения с ограниченной или полуограниченной областью определения. Исключения составляют модели AR и PACGAN, где классификация однозначно указывает на тип VI, соответствующий экспоненциальным или квазинормальным распределениям со сдвигом.
На основе оцененных характеристик для каждой из последовательностей выполнено моделирование с использованием соответствующего распределения Пирсона. После генерации по каждой моделируемой последовательности проведен расчет характеристик и сравнение с оригиналом по относительным отклонениям. Результаты усреднены по 500 независимым прогонам и представлены в таблице 2.
Таблица 2
Относительные отклонения статистических характеристик моделируемых последовательностей от исходной
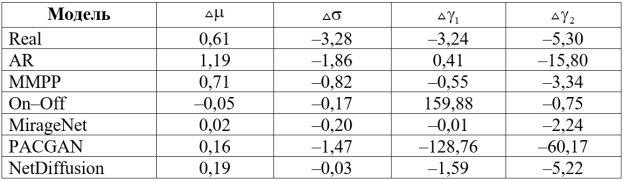
В большинстве случаев отклонения по всем характеристикам не превышают ±3 %, что подтверждает способность метода воспроизводить в статистическом смысле поведение входных последовательностей. Большие значения асимметрии наблюдаются у моделей ON–OFF и PACGAN, где форма распределения близка к симметричной или периодически модулируемой, что ограничивает точность аппроксимации в рамках одной выборки фиксированной длины. В то же время даже при таких условиях метод обеспечивает практически те же значения дисперсии и эксцесса.
На рис. 1 представлены реальные сетевые данные (Real) трафика МВС, отличающиеся нерегулярным характером с редкими, но высокоинтенсивными пиками активности. Распределение значений выражено асимметрично, а наличие значительных выбросов указывает на типичные для сетей явления перегрузки или сетевых атак.
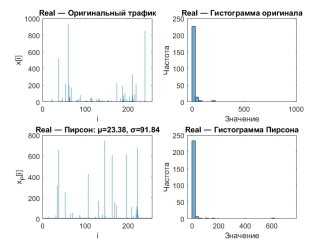
Рис. 1. Временная реализация и распределение значений реального сетевого трафика (Real) и аппроксимации распределением Пирсона
В отличие от реального трафика, модель AR (рис. 2) демонстрирует более предсказуемую структуру с постепенным снижением плотности событий. Поток характеризуется равномерным распределением активности и отсутствием резких изменений (выбросов), что типично для стационарных линейных процессов.
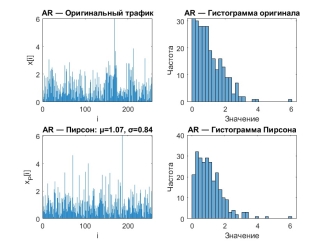
Рис. 2. Временная реализация и распределение значений трафика, сгенерированного авторегрессионной моделью (AR), и аппроксимации распределением Пирсона
Модель MMPP (рис. 3) формирует последовательность с чередованием фаз высокой и низкой нагрузки, что приводит к переменной интенсивности передачи трафика. Такая структура отражается в асимметричном распределении с удлинённым хвостом и хорошо подходит для описания трафика, подверженного фазовым переходам.
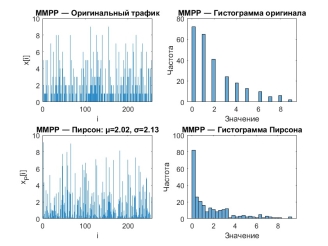
Рис. 3. Временная реализация и распределение значений трафика, сгенерированного моделью MMPP, и аппроксимации распределением Пирсона
В свою очередь, модель ON-OFF (рис. 4) генерирует дискретный поток, состоящий из чередующихся состояний активности и простоя. Гистограмма подтверждает жёсткую двухуровневую структуру, соответствующую типовым сценариям с прерывистой передачей данных, например, в сенсорных сетях.
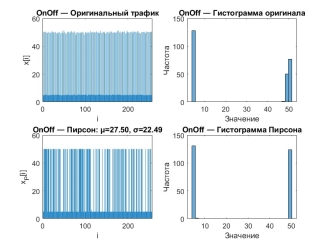
Рис. 4. Временная реализация и распределение значений трафика, сгенерированного моделью ON–OFF, и аппроксимации распределением Пирсона
MirageNet (рис. 5) демонстрирует многомодальное поведение, где зоны высокой активности чередуются с участками низкой плотности. Такая структура приводит к распределению с несколькими выраженными пиками и отражает сложные сценарии с разнородной генерацией пакетов.
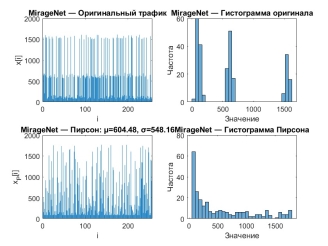
Рис. 5. Временная реализация и распределение значений трафика, сгенерированного моделью MirageNet, и аппроксимации распределением Пирсона
На рис. 6 модель PACGAN формирует трафик с равномерной плотностью событий и распределением, приближённым к нормальному.
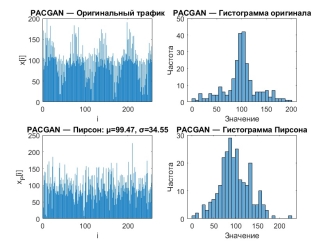
Рис. 6. Временная реализация и распределение значений трафика, сгенерированного моделью PACGAN, и аппроксимации распределением Пирсона
Наблюдаемые различия между моделями охватывают несколько характерных типов поведения сетевого трафика — от стационарных и линейных до фазово-зависимых и дискретных. Несмотря на разнообразие форм, классификация по критерию Пирсона сохраняет характеристики временных последовательностей и их распределений, что позволяет применять данный подход для идентификации и имитации сетевых трафиков различного вида.
Заключение
Проведенное исследование показало, что система распределений Пирсона может быть использована для моделирования сетевого трафика различного вида без необходимости знания внутреннего механизма формирования последовательностей данных. Метод основан на восстановлении функции плотности вероятности по первым четырем моментам и автоматической классификации типа распределения из семейства распределений Пирсона. Такая схема позволяет воспроизводить поведение потока транзакций с высокой степенью точности в отношении среднего значения, дисперсии, асимметрии и эксцесса. Метод может применяться в прикладных задачах анализа зашифрованного или агрегированного сетевого трафика, когда глубокий анализ пакетов, например, по DPI, недоступен.
Эксперименты подтвердили применимость метода к широкому спектру моделей, включая как генераторы (AR, MMPP, ON–OFF), так и модели, имитирующие реальные источники трафика (MirageNet, PACGAN, NetDiffusion). В большинстве случаев отклонения по основным статистическим характеристикам не превышали 3 %, что соответствует требованиям к воспроизведению поведения потока транзакций в задачах тестирования, анализа и моделирования сетевого трафика.
В перспективе предполагается совершенствование метода за счет включения трендовых компонент. Современные исследования указывают на наличие скрытых закономерностей и структурных смещений в сетевых последовательностях транзакций. Разработка комбинированной схемы, объединяющей вероятностное моделирование с воспроизведением динамики тренда, позволит тестировать существующие и разрабатывать новые методы обнаружения долгосрочных трендов в трафике, включая выявление скрытых аномалий и структурных изменений.
Благодарности
Данная работа финансировалась за счет средств бюджета в рамках государственного задания Министерства науки и высшего образования РФ № FSWF-2025–0010 «Разработка научно-технических основ создания программных и аппаратных решений для управления объектами энергетики с использованием цифровых двойников и технологий искусственного интеллекта» и написана под руководством доктора технических наук, профессора Бехтина Ю. С. Никаких дополнительных грантов на проведение или руководство данным конкретным исследованием получено не было. Авторы данной работы заявляют, что у них нет конфликта интересов.
Литература:
1. Павлович А. В., Дубровская Е. А., Баланев К. С., Бехтин Ю. С. Стабилизация пульсирующего сетевого трафика многомашинных вычислительных систем… // Технологии будущего… М.: НИУ «МЭИ», 2025. С. 348–359.
2. Баланев К. С., Бехтин Ю. С. Сравнительный анализ прогнозирования сетевого компьютерного трафика с использованием RNN, ARIMA моделей и вейвлет-преобразования… Казань: КГЭУ, 2024. С. 739–742.
3. Willinger W., Paxson V., Riedi R. H., et al. Long-range dependence and heavy tail behavior in Internet traffic. IEEE/ACM Transactions on Networking, 1997.
4. Park K., Willinger W. (Eds.). Self-similar network traffic and performance evaluation. Wiley, 2000.
5. Papagiannaki K., et al. Long-term forecasting of Internet backbone traffic. IEEE Transactions on Neural Networks, 2005.
6. Heffes H., Lucantoni D. M. A Markov Modulated Characterization of Packetized Voice and Data Traffic and Related Statistical Multiplexer Performance. IEEE Journal on Selected Areas in Communications, 1986.
7. Karagiannis T., Molle M., Faloutsos M. Long-range dependence: now you see it, now you don't! IEEE GLOBECOM, 2002.
8. Norros I. On the use of fractional Brownian motion in the theory of connectionless networks. IEEE Journal on Selected Areas in Communications, 1995.
9. Pearson K. Contributions to the Mathematical Theory of Evolution. Philosophical Transactions of the Royal Society of London, 1895.

