Presently and in the future, waterway transport activities will continue to develop strongly thanks to its low cost advantage, however, waterway transport activities also have many potential risks. For many different reasons, waterway vehicles (ships, boats, canoes, etc.) can be penetrated by water into the cargo hold, slowing down the transportation process and even causing sinking in severe cases. Based on the theory of ships and the theory of swimming vehicles, the author develops the calculation contents using integral models to simplify and make the calculation results more accurate. On that basis, the article presents the sequence of contents to evaluate the swimming ability of waterway vehicles when water penetrates into the cargo hold through physical parameters: speed, time, and the distance the ship can swim over time.
Keywords: boat, swimming ability, sinking, water ingress, swimming speed, water flow rate, swimming distance, swimming time.
- Introduction
Nowadays, water transportation means are increasingly asserting their important role in the trade of goods between regions due to the advantage of low transportation costs. According to statistics from the Vietnam Inland Waterway Administration, the cost of waterway transportation is only half that of rail and a quarter that of road transport. In addition to the advantage of low transportation costs, inland waterway transportation also poses many risks of accidents. According to statistics from the Vietnam Inland Waterway Administration [1], from 2015 to 2023, there were 662 accidents nationwide, resulting in 418 deaths and 78 injuries. One of the common causes of waterway traffic accidents is the use of old transportation vehicles that have undergone multiple modifications, with the hull condition severely deteriorated due to rust [11]. When physical interactions occur, it easily leads to the appearance of cracks and holes in the hull, allowing water to enter the cargo hold and causing the vessel to sink.
Ship theory has been presented in many research works [2], [5], [4],, etc., however, according to the author's research, there has not been any serious study on this issue in the world and in Vietnam up to the present time. In this article, the author presents a method for assessing the swimming capability of water transport vehicles when water enters the cargo compartment, based on the theoretical foundation of swimming vehicles [6], [8], [10], etc., This is done through parameters such as speed reduction, distance, and the time the vehicle can swim with water entering a specific transport vehicle. From this, recommendations are made for operators to make decisions on how to handle situations when water enters the cargo hold.
2. Research methods
Below, the author presents the theoretical basis for the swimming of ships to determine the basic physical parameters necessary for assessing the swimming capability of waterway transport vehicles in situations where cracks or holes appear in the hull, causing water to flood into the cargo hold.
2.1 The flow of water entering the cargo hold through a hole in the hull of the ship over time t.
According to [7, pages 56–64], the flow of water entering the cargo hold of the ship through a hole in the hull at a specific time t is determined by the following expression:
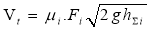
V t — The water flow entering the cargo hold of the ship through a hole in the hull over time t.
µ i — the flow coefficient, (0,65 -0,68);
F i — the area of the hole in the hull of the ship through which water enters the cargo hold, m 2 ;
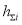
g — gravitational acceleration, m/s 2 ;
The total pressure head is understood as the sum of the static pressure head and the dynamic pressure head, along with the back pressure created by the excess air pressure in the vessel or the amount of water in the hull of the vessel. The total pressure head is determined by the following expression [7]:
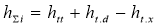
In that,
htt —
hydrostatic pressure column, is equal to the distance from the center of the hole on the hull of the ship to the waterline of the vessel.
h
tt = d3;
ht.d
— hydraulic pressure column (determining formula
ht.d
= 0,5.a.
v
2/g), m; in that
v
— the swimming speed of the ship relative to the water surface., m/s; a = 1,1–1,2 — dimensionless empirical coefficient;
ht.x
— he pressure column converted with respect to the center of the hole on the hull of the ship depends on the amount of water that enters the cargo hold of the ship, determined to satisfy the following condition:
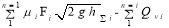
- The amount of water remaining in the cargo hold of the ship over time t.
The amount of water accumulated in the cargo hold of the ship up to a certain point in time is determined by the following expression [7, pages 56–64]:
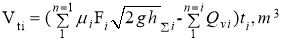
2.3 The speed of a ship depends on the amount of water that enters its cargo hold.
The swimming speed of the ship depends on the amount of water that enters the cargo hold, which will change as follows:
If the ship is not equipped with a pump to remove water from the cargo hold — the amount of water entering the cargo hold increases over time, causing the ship to gradually sink, the hydrodynamic resistance to increase, the ship's speed to decrease towards 0, and the ship will eventually sink. The ship travels a distance S 1 .
If when opening the pump to drain water from the cargo hold of the ship, two cases occur:
+ The pump capacity is less than the water inflow into the cargo hold, causing the amount of water in the cargo hold to increase, which in turn increases the drag force acting on the hull, gradually reducing the vessel's speed to zero. This case is similar to the previous one, but the ship will be able to travel a longer distance S 2 > S 1 .
The swimming speed of the ship depends on the amount of water that enters the cargo hold, determined by the following expression [7, pages 56–64]::
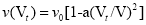
v (V t ) — The swimming speed of the ship depends on the amount of water entering the cargo hold over time t i ;
V t — the volume of water accumulated in the cargo hold of the ship, m 3 ;
V — the water displacement of a ship, m 3 ;
v o — The swimming speed of the ship when no water enters the cargo hold of the ship, m/s;
a — The non-integer coefficient has a value: 11–13.
- Determining the time a ship can stay submerged underwater when a specified amount of water enters the cargo hold of the ship.
Considering the following relationship:
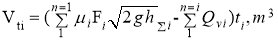
V t — The maximum value is exactly equal to the volume of the ship: V tt = 16 m 3 , from this, we can deduce the total time t that the ship can sail.
2.5 Determine the distance that the ship can travel S.
- The distance a boat can travel over a specified time t is as follows: S = v tb .t, m. (6)
The average swimming speed of a ship:
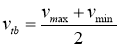
The maximum time a ship can float is precisely at the moment it is completely submerged in water, meaning the volume of the ship is fully filled with water.
The distance that a boat can travel is determined as follows:
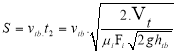
3. Research results and discussion
Now let's consider any swimming vehicle (ship, boat, canoe, amphibious vehicle, etc.) with a cross-sectional profile presented as shown in Figure 1 below
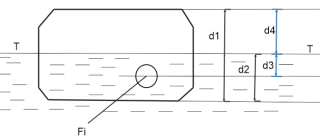
Fig. 1 Cross-sectional diagram of the ship
In that:
d1 — the height of the ship, m;
d2 — the height of the waterline T-T of the ship, m;
d3 — The distance from the center of the hole on the hull of the ship to the waterline T-T, m;
d4 — The distance from the waterline to the upper edge of the ship's side, m;
F i — the area of the hole on the hull of the ship, m 2 .
The hypothesis is that the ship has the initial technical specifications presented in Table 1 below:
Table 1
Calculation parameters for assessing the swimming capability of a vessel with a hole in the hull
|
№ |
Specifications |
Symbol |
Value |
Unit |
|
1 |
The weight of the ship |
G |
14000 |
kg |
|
2 |
The cargo hold volume of the ship |
V tx |
16,3 |
m 3 |
|
3 |
The water displacement volume of a ship |
V cn |
14 |
m 3 |
|
4 |
The actual water depth of the vessel |
d2 |
1,1 |
m |
|
5 |
The reserve buoyancy of a ship |
D dt |
15,6 |
% |
|
6 |
The maximum swimming speed of a ship |
v 0 |
2,8 |
m/s |
|
7 |
The height of the ship |
d1 |
2,3 |
m |
|
8 |
The distance from the center of the hole to the waterline of the ship |
d3 |
0,5 |
m |
|
9 |
The distance from the waterway T-T to the side of the vessel |
d4 |
1,2 |
m |
|
10 |
The area of the hole in the hull of the ship |
F i |
0,003 |
m 2 |
|
11 |
The pump capacity for extracting water from the cargo hold of the ship |
Q |
180 |
liters/minute |
The calculations below are conducted under the assumption that the water transport vehicle is operating in still water, meaning the flow velocity is zero v dc = 0 m/s, The wind speed is zero v gi = 0 m/s, standard atmospheric pressure 1 at.
3.1 Determine the water flow entering the cargo hold of the ship through the hole over time t i .
The flow of water entering the cargo hold of the ship through a hole in the hull over time t i can be determined by the expression.
On the other hand, we know that at the initial moment, due to the negligible amount of water entering the cargo hold, we can consider h t.x ≈ 0 m, The boat is still moving at its maximum initial speed v 0 = 2,8 m/s. At that time:
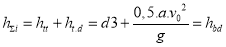
At the moment the ship sinks, the swimming speed of the vessel is zero, so
h
t.d
= 0.5.a.v²/g = 0 m, and
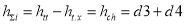
Observing, we see that the values of h tt and h t.x increase proportionally over time ti, which means that the flow of water entering the cargo hold of the ship through the hole in the hull increases proportionally over time ti. In contrast, h t.d = 0.5.a.v²/g will gradually decrease over t i . This means that through the average water flow, we can determine the flow of water entering the cargo hold through the gap over time t i as follows:
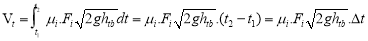
The total value of the average pressure column h tb is determined by the expression h tb = ( h bd + h ch )/2 = [(d3+0,5.a.v2/g) + ( h tt — h t.x )]/2 = [(d3+0,5.a. v 2 /g) + (d3 + d4)]/2, m.
Thus, we can rewrite expression (10) as follows:
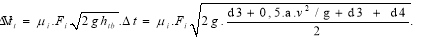
The graph describes the relationship between the water flow entering the cargo hold through a hole in the hull of the ship with an area of Fi = 0,003 m², as shown in Figure 2 below:
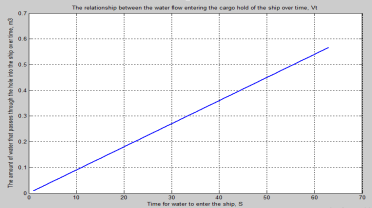
Fig. 2 The relationship between the water flow entering the cargo hold of the ship over time t i
Observing the graph, we see that at the time of measuring, the water flow entering the cargo hold of the ship is approximately 0.009 m³/s, which is about 9 liters per second.
3.2 The amount of water that enters the ship through holes in the hull and accumulates in the cargo hold over time t.
As stated above, the amount of water that enters the cargo hold of the ship when the pump operates is determined by the following expression:
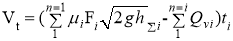
On the other hand, we know that the total column pressure value h∑i will change from the minimum value d3 to the maximum value d4+d3, so the average total column pressure is determined as follows:
h tb = (d3+d4)/2= [d3+(d1-d2)]/2 , m (13)
Thus, the amount of water entering the hull can be determined by the integral of the water flow into the hull over the time period from t 1 to t 2 based on the average pressure value, that is:
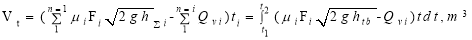
The amount of water that enters the cargo hold of the ship when the ship is not equipped with a bilge pump or when the pump is not turned on is determined as follows:
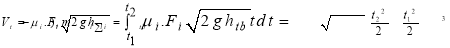
The graph describes the relationship between the flow of water entering the cargo hold of the ship and the water remaining in the cargo hold of the ship V t over time t, as shown in Figure 3.3 below:
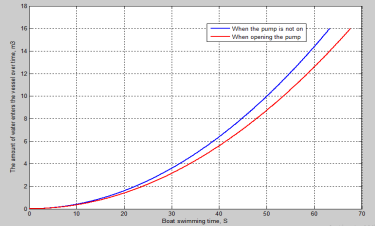
Fig. 3. The relationship between the volume of water V t entering and remaining in the cargo hold of the ship over time t
As stated above, the decrease in the speed of the vessel depends on the amount of water entering the cargo hold of the vessel over time, determined by expression (4). From expressions (10) and (4), it can be inferred that:
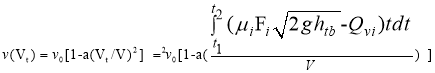
The graph depicting the decrease in the speed of the ship over time is presented in Figure 4 below:
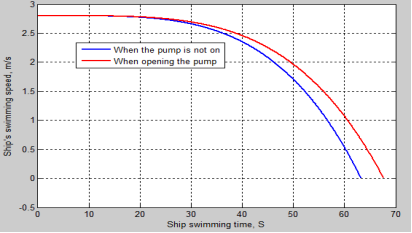
Fig. 4. The decrease in the swimming speed of the vessel over time t
- Determine the time a ship can float when a specified amount of water enters the cargo hold of the vessel.
Considering the relationship:
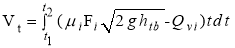
The value V t eaches its maximum value equal to the volume of the ship: V = 16 m 3 . If we choose the starting time of the survey to coincide with the time the water begins to enter the cargo hold of the ship, that is, t 1 = 0, and if the pump to remove water from the cargo hold of the ship is not turned on, then:
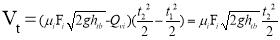
In that:
µ i = 0,65÷0,68; F i = 0,003 m 2 ; g = 10 m/s 2 ; h tb = (d3+d4)/2 = [d3+(d1-d2)]/2= [0,5+(2,3–1,1)]/2≈ 0,823 m;
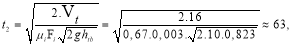
If the ship is equipped with a pump to remove water from the cargo hold with a suction capacity of 180 liters per hour, the time the ship can float is determined as follows:

- Determining the distance S that the ship can travel in time t.
The distance S that the boat can travel in time t is determined as follows:
S = v tb .t.
The average swimming speed of the vessel is determined by the expression below:
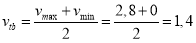
The maximum time a ship can float is precisely when the ship is completely submerged in water, meaning the water has filled the entire volume of the ship.
So the distance that the boat can travel is:
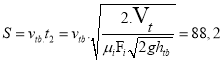
The function describing the distance traveled by the train over time is a simple linear function represented in Figure 3.5 below:
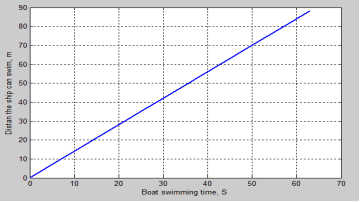
Fig. 5. The relationship between the distance S traveled by the boat over time t
Comment on the calculated contents:
— Observing graph 3.2, we see that the water flow through the hole into the cargo hold at the initial moment is 0.009 m³ = 9 liters/s. Over time, the total pressure column increases, and the water flow through the hole into the cargo hold increases linearly with time t;
— From graph 3.3, we can see that the water accumulation in the cargo hold of the ship over time t, when the pump is not turned on to remove water from the cargo hold, is represented by the blue line, which increases according to a nonlinear function. The water accumulation time is 63 seconds, while the red line represents the scenario when the pump is turned on to remove water from the cargo hold, with the ship operating for 68 seconds.
— From graph 3.4, it can be observed that the swimming speed of the ship decreases from 2.8 m/s to zero along the blue line, following a nonlinear function. The deceleration time from 2.8 m/s to zero is 63 seconds, while the red line represents the time when the pump is turned on to drain water from the ship's cargo hold, with a deceleration time from 2.8 m/s to zero of 68 seconds.
— Graph 3.5 describes the distance a ship can travel; it is a linear function. The distance S the ship can travel is 88.2 m corresponding to a swimming time of 63 s. If the pump is turned on to remove water from the cargo hold, the ship will be able to travel a distance of 95.2 m corresponding to a swimming time of 68 s.
4. Conclusion and recommendations
From the results of the survey calculations, several conclusions can be drawn as follows:
The article conducted calculations to investigate the characteristic parameters affecting the swimming ability of the vessel when water infiltrates the cargo hold over time t, starting from the moment water begins to enter until the vessel is completely submerged. The calculation results are presented in the form of data and visual graphs, making it easy to assess and observe the nature of the changes in the parameters, including:
— The flow of water leaking through the hole in the hull into the cargo hold at any given time t i ;
— The accumulated water flow in the cargo hold over time t i ;
— The decrease in the ship's swimming speed over time t;
— Determining the time t that the ship can continue to swim;
— Determining the distance S that the ship can swim before completely sinking underwater.
However, the calculation results do not fully account for the environmental conditions that may affect the vessel's swimming dynamics. Specifically, the calculated results are based on the theoretical framework of swimming vehicles under the following limiting conditions: still water surface, flow velocity v dc = 0 m/s, no wind, and atmospheric pressure at standard conditions of 1 atm.
If the survey calculations are conducted in more complex environmental conditions, especially when considering the water flow velocity v dc ≠ 0 m/s and the presence of wind, it is necessary to take into account both the wind speed and the angle of the wind hitting the side of the vessel [12]. This makes the problem significantly more complex, as the drag force acting on the frontal area of the ship will increase or decrease depending on the vectors of the flow velocity and wind speed. The author would like to address this issue in upcoming research projects.
References:
1. https://www.baogiaothong.vn/hon-300-diem-nguy-co-xay-ra-tai-nan-duong-thuy-1922401922404 2518393775.htm.
2. K. J. Rawson, E. C. Tupper. Basic ship theory. Newdelhi 2001.
3. Першиц Р. Я. Управляемость и управление судном. Л.: Судостроение, 1983.
4. Снопкова В. И. Управление судном. Санкт-Петербург. 2004.
5. Соболев Г. В. Управляемость корабля и автоматизация судовождения. Л.: Судостроение, 1976.
6. Соларев Н. Ф. и др. Управление судами и составами. М.: Транспорт, 1983.
7. А. П. Степанов, (1983), Конструирование и расчет плавающих машин, Москва.
8. Д. В. Дорогостайстайский, М. М. Жученко, (1976), Теория и устройство судна, Ленинград.
9. В. Б. Жинкин, (2002), Теория и устройство корабля, С — Петербург.
10. П.А Нутович (1970) Водометные движители малых судов, Лелинград.
11. https://knowledgeofsea.com/assessing-and-recording-damage-to-the-ship/

