В данной работе рассмотрены преимущества использования интерактивных иллюстраций и основные способы их разработки при помощи пакета компьютерной алгебры WolframMathematica.
Ключевые слова: Wolfram Mathematica, система компьютерной алгебры, интерактивная компьютерная графика, .NET Framework, Wolfram|Alpha, Computable Document Format, Wolfram.NET/Link, MathLink.
Введение
Наглядность представления материала — одно из необходимых требований для его корректного понимания. Особенно, если этот материал изложен в научном труде или используется в образовательном процессе. Применение в данном случае интерактивной компьютерной графики позволяет обеспечить максимальную наглядность, так как позволяет взглянуть на проблему с разных сторон.
Нередко для подобных иллюстраций необходимы сложные математические, геометрические, статистические и аналитические расчёты. В данном случае огромную пользу принесут программы математического моделирования и системы компьютерной алгебры, примерами которых являются Mathcad, Wolfram Mathematica и Matlab.
Возможность создания интерактивной графики широко обеспечивается в системе компьютерной алгебре Wolfram Mathematica. Это позволяет объединить всю вычислительную и алгоритмическую мощность Wolfram Mathematica для расчёта и прорисовки динамически изменяющихся элементов интерактивной графики: символьных и числовых вычислений или графиков функций.
Wolfram Mathematica
Система компьютерной алгебры Wolfram Mathematica была разработана компанией Wolfram Research. Она содержит множество функций, как для аналитических преобразований, так и для численных расчётов. Кроме того, программа поддерживает работу с графикой и звуком, включая построение двух- и трёхмерных графиков функций, рисование произвольных геометрических фигур, импорт и экспорт изображений и звука.
Кроме того, Mathematica это интерпретируемый язык функционального программирования. Mathematica поддерживает и процедурное программирование с применением стандартных операторов управления выполнением программы (циклы и условные переходы), и объектно-ориентированный подход. Mathematica допускает отложенные вычисления. Также в систему Mathematica можно задавать правила работы с теми или иными выражениями [1].
Основа Mathematica гибкий символьный язык, поддерживающий множество парадигм программирования, продвинутые инструменты отладки, автоматическое проектирование интерфейса и многое другое. Он упрощает весь процесс разработки от дизайна до внедрения. Mathematica всё данные, программы, формулы, графики, документы представляет в виде символьных выражений [2].
Wolfram Mathematica это программное обеспечение, не только для математических вычислений, это гораздо больше: от моделирования и симуляции, визуализации, документации, до создания веб-сайтов. Wolfram Mathematica обладает возможностью осуществлять вызовы функций и принимать вызовы с C,.NET, Java и других языков, генерировать C код, компилировать автономные библиотеки и исполняемые файлы [3].
Все вычисления в Wolfram Mathematica находятся в блокнотах и имеют расширение .nb. В блокнотах находятся как и код, так и результаты вычислений. Блокноты разбиты на ячейки различного типа: ячейки ввода (в них задаются команды, которые будут вычислены), ячейки результата (в них выводится результат вычислений) и другие ячейки (ячейки с текстом, заголовки и все остальное) [3]. Пример блокнота Wolfram Mathematica представлен на рис. 1.
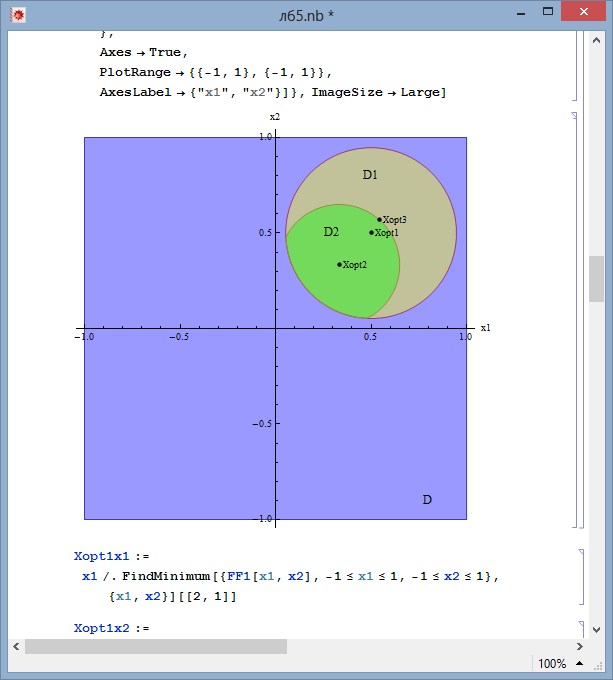
Рис. 1. Демонстрация блокнота Wolfram Mathematica
Wolfram|Alpha API
Система Wolfram|Alpha является базой знаний и набором вычислительных алгоритмов. Wolfram|Alpha не возвращает перечень ссылок, основанный на результатах запроса, а вычисляет ответ, основываясь на собственной базе знаний, которая содержит данные о математике, физике, астрономии, химии, биологии, медицине, истории, географии, политике, музыке, кинематографии, а также информацию об известных людях и интернет-сайтах. Он способен переводить данные между различными единицами измерения, системами счисления, подбирать общую формулу последовательности, находить возможные замкнутые формы для приближенных дробных чисел, вычислять суммы, пределы, интегралы, решать уравнения и системы уравнений, производить операции с матрицами, определять свойства чисел и геометрических фигур [4]. В основе Wolfram Alpha лежит программа компьютерной алгебры Wolfram Mathematica.
Разработчиками Wolfram|Alpha было создано API для обеспечения возможности встраивания результатов выполнения запросов к системе в веб-сайты, прикладные и развлекательные приложения. Для некоммерческого использования данное API бесплатно. К сожалению, возможно выполнение только одной команды, что, в свою очередь, делает невозможным использование модулей и функций.
Демонстрация выполнения запроса в системе Wolfram|Alpha представлена на рис. 2. При использовании же API, ответ возвращается в виде XML.
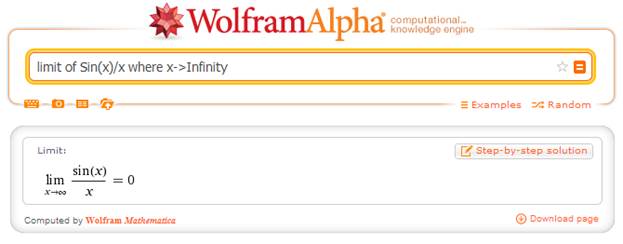
Рис. 2. Демонстрация работы Wolfram|Alpha
Computable Document Format
Формат вычисляемых документов (Computable Document Format или CDF) — это электронный формат документов, созданный с целью облегчения создания динамически сгенерированного интерактивного контента. Формат разработан компанией Wolfram Research. Формат вычисляемых документов предусматривает такие графические элементы пользователя как ползунки, меню и кнопки. Содержимое документа обновляется с использованием встроенной вычислительной подсистемы при взаимодействии с графическими элементами пользователя. В документе могут использоваться текст, таблицы, изображения, звуки и анимации. Формат CDF предусматривает использование печатной вёрстки и технических обозначений системы Wolfram Mathematica. Также поддерживаются компоновки документа с разбивкой на страницы, со структурной детализацией и режим слайд-шоу. Стилистическое оформление документа можно контролировать с использованием каскадных таблиц стилей.
CDF файлы можно просматривать с помощью бесплатной программы CDF Player, которую можно загрузить с сайта компании Wolfram Research. В отличие от статических форматов, таких как PDF и предварительно сгенерированного информационного материала в форматах, таких как Adobe Flash, и благодаря тому, что программа CDF Player целиком содержит библиотеку времени исполнения системы Wolfram Mathematica, содержимое документа может генерироваться в ответ на действие пользователя с помощью любых алгоритмов или визуализационных функций, которые можно описать в системе Wolfram Mathematica. Это делает CDF особенно уместным для научного, инженерного и другого технического материала, а также электронных учебников [5].
Файлы формата CDF могут быть созданы из существующих блокнотов Wolfram Mathematica или с нуля. Они могут содержать абсолютно все, что может быть создано в блокноте Wolfram Mathematica. Основное отличие между блокнотом Wolfram Mathematica и файлом формата.cdf заключается в возможности взаимодействия с документом при его просмотре в CDF Player. Файлы блокнота в Wolfram Mathematica (файлы с расширением .nb) при просмотре в CDF Player отображаются как статичные документы, однако в файле формата.cdf любой объект, созданный с помощью функции Manipulate, обладает полной интерактивностью при просмотре в CDF Player [6].
Примером данной реализации интерактивной иллюстрации является разработанное программное обеспечение для поиска кривой Парето и компромиссной кривой (рис. 3) для численной минимизации критериев.
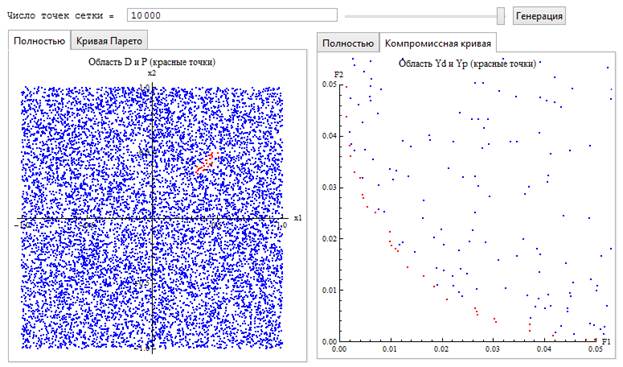
Рис. 3. Пример создания CDF файла
Wolfram.NET/Link
Для обмена данными между Wolfram Mathematica и другими программами существует специально разработанный протокол MathLink. Модуль .NET/Link позволяет программисту избегать низкоуровневых деталей этого процесса и позволяет программисту писать высокоуровневый код под .NET Framework. Этот набор библиотек позволяет с помощью одной команды отправить какой-либо запрос ядру Wolfram Mathematica и получить ответные данные с помощью другой. В данном случае, возможно использовать любой язык программирования, поддерживаемый.NET Framework. Разработка кода возможна и на языке Си без использования технологий.NET Framework, но уже с применением самого MathLink.
Основной недостаток применения .NET/Link состоит в том, что хотя сама библиотека занимает всего один файл (Wolfram.NETLink.dll), программа, без предустановленной среды Wolfram Mathematica, успешно функционировать не будет. Плюсом же данного подхода является возможность исполнения любых команд и, даже, групп команды языка Mathematica и возвращение результата вычислений. В том числе и графического [7].
Для работы с ядром Wolfram Mathematica проще всего использовать компонент MathKernel из пространства имён Wolfram.NETLink: По умолчанию свойство CaptureGraphics этого компонента задано как false. Если результат вычислений ожидается графический, то это свойство необходимо инвертировать.
Передача команд ядру Wolfram Mathematica осуществляется методом Compute компонента MathKernel. Результат вычислений помещается в свойство Result компонента. Графический результат — в свойство Graphics. Таким образом, код под .NET Framework сводится к минимуму. Примером служит программное обеспечение для синтез ПИ-регулятора квазимаксимальной степени устойчивости и заданной колебательности (рис. 4).
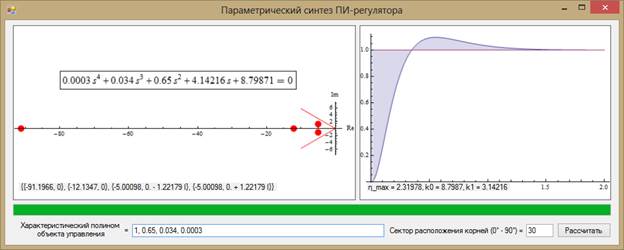
Рис. 4. Демонстрация работы приложения с библиотекой.NET/Link
Заключение
В результате данной работы были рассмотрены возможности системы компьютерной алгебры Wolfram Mathematica для создания и внедрения интерактивной компьютерной графики. Так же были рассмотрены примеры их реализации. Wolfram Mathematica может стать хорошим инструментом для студентов и молодых учёных для иллюстрации своих работ. К сожалению, основные минусы Wolfram Mathematica — высокая цена и плохая мобильность — могут препятствовать активному использованию данного программного пакета.
Литература:
1. Mathematica [Электронный ресурс]: Википедия. — США: wikipedia.org, 2013. — Режим доступа: http://ru.wikipedia.org/wiki/Mathematica, свободный. — Дата обращения 08.07.2013.
2. Wolfram Mathematica: знакомство [Электронный ресурс]: Хабрахабр. — Россия: habrahabr.ru, 2011. — Режим доступа: http://habrahabr.ru/post/113588/, свободный. — Дата обращения 08.07.2013.
3. Введение в Wolfram Mathematica [Электронный ресурс]: Хабрахабр. — Россия: habrahabr.ru, 2013. — Режим доступа: http://habrahabr.ru/post/180925/, свободный. — Дата обращения 08.07.2013.
4. WolframAlpha [Электронный ресурс]: Википедия. — США: wikipedia.org, 2013. — Режим доступа: http://ru.wikipedia.org/wiki/WolframAlpha, свободный. — Дата обращения 08.07.2013.
5. Формат вычисляемых документов [Электронный ресурс]: Википедия. — США: wikipedia.org, 2013. — Режим доступа: http://ru.wikipedia.org/wiki/ %D0 %A4 %D0 %BE %D1 %80 %D0 %BC %D0 %B0 %D1 %82_ %D0 %B2 %D1 %8B %D1 %87 %D0 %B8 %D1 %81 %D0 %BB %D1 %8F %D0 %B5 %D0 %BC %D1 %8B %D1 %85_ %D0 %B4 %D0 %BE %D0 %BA %D1 %83 %D0 %BC %D0 %B5 %D0 %BD %D1 %82 %D0 %BE %D0 %B2, свободный. — Дата обращения 08.07.2013.
6. Создание файла формата CDF (Computable Document Format) [Электронный ресурс]: Хабрахабр. — Россия: www.kobriniq.ru, 2013. — Режим доступа: http://www.kobriniq.ru/mathematica/rukovodstvo-sozdanie-fayla-formata-cdf-computable-document-format, свободный. — Дата обращения 08.07.2013.
7. Используем возможности Wolfram Mathematica в.NET приложениях [Электронный ресурс]: Хабрахабр. — Россия: habrahabr.ru, 2012. — Режим доступа: http://habrahabr.ru/post/154169/, свободный. — Дата обращения 08.07.2013.

