Современные спутники связи функционируют на различных орбитах, предоставляя широкий спектр услуг, включая мобильную связь, подключение к Интернету, телевидение, навигацию и другие. Для обеспечения высокого качества связи и бесперебойной работы спутников необходимо гарантировать их стабильное и точное положение на орбите. Одним из важнейших факторов, влияющих на движение спутников, является воздействие внешних сил, среди которых особенно значимым является солнечное давление. Учитывая малую сопротивляемость космического пространства, малейшие внешние силы, такие как солнечное давление, могут приводить к смещению спутников с их орбит. Поэтому исследование солнечного давления и его влияния на спутники связи имеет большое значение для обеспечения точного управления их орбитами и для минимизации возможных ошибок, связанных с орбитальными маневрами.
В рамках данного исследования проведены расчёты силы солнечного давления, действующей на спутник связи «ТуркменАлем 52Е», который работает на геостационарной орбите на позиции 52° в. д. С помощью этих расчётов проанализировано влияние солнечного давления на спутник и его орбитальное движение, что является важным для точности спутниковых услуг связи.
Влияние солнечного давления на спутники
Солнечное давление зависит от нескольких факторов, таких как положение Солнца относительно спутника, масса спутника, площадь поверхности спутника, а также отражающие и рассеяющие свойства материалов, из которых изготовлена поверхность спутника. Основной проблемой при расчёте солнечного давления является точное определение расстояния между спутником и Солнцем в каждый момент времени, а также учёт угла падения солнечных лучей.
Формула для расчёта давления солнечного света выражается через световой поток, который на расстоянии 1 астрономической единицы (АЕ) от Солнца равен 1367 Вт/м². Важно отметить, что для всех спутников на геостационарной орбите расстояние от спутника до Земли значительно меньше, чем расстояние от Земли до Солнца, что позволяет в расчётах использовать постоянное значение для этого расстояния — 1 АЕ, равное 149 597 871 км.
Общая формула для расчёта давления солнечного света:
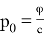
Здесь φ — световой поток, который равен φ=1367 Вт/м 2 на расстоянии 1 А.Е. (астрономическая единица) от Солнца, c≈3x108 м/с — скорость света. Тогда,
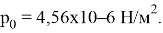
Сила давления, оказываемая солнечным давлением в нормальном направлении на спутники, движущиеся по геостационарной орбите, рассчитывается по следующей формуле:
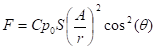
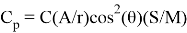
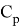
Здесь C=1+ɳ; ɳ — коэффициент рассеяния. Эта величина меняется в зависимости от материала рассеивающей поверхности. Для солнечной панели рассматриваемого нами спутника эта величина равна 0,3. S — площадь поверхности спутника, фактически площадь солнечной батареи, A — большая полуось орбиты Земли, r — расстояние между спутником и Солнцем, θ — угол падения солнечных лучей. Как видно из рисунка ниже (рис. 1), тангенциальная составляющая силы солнечного давления перпендикулярна орбите спутника. Это означает, что динамическое воздействие тангенциальной силы на спутник за полный оборот равно нулю, т. е. оно не влияет на орбиту спутника. Поэтому в данной работе мы рассматривали только нормальное направление силы давления, создаваемой солнечным светом согласно формуле (2). Также в расчетах для площади поверхности спутника учитывалась только площадь солнечной панели (батареи), так как большую часть площади поверхности спутника занимает солнечная батарея. Также это важно для сравнения расчетных значений коэффициента солнечного давления с коэффициентом, который получается с солнечного датчика спутника.
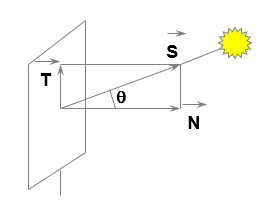
Рис. 1
Расчёты и алгоритм определения координат Солнца
Используя формулу (2), для расчета силы давления, создаваемой солнечными лучами, необходимо определить изменение расстояния между спутником и Солнцем с течением времени. Поскольку расстояние между спутником и Землей очень мало по сравнению с расстоянием между Солнцем и Землей, в расчетах учитывалось расстояние между Солнцем и Землей. Существует несколько теоретических и экспериментальных методов определения координат Солнца. В наших расчетах используются формулы, приведенные в Astronomical Almanac. Astronomical Almanac, основанный на методе Ньюкомба, дает формулы для определения координат Солнца с точностью 0,01 % на период 1950–2050г. Эти формулы определены относительно экваториальной системы координат, при этом ось X направлена на Солнце в день весеннего равноденствия 2000 года. Сначала определяются точные координаты Солнца на дату 01.01.2000, 12:00 (UT), затем вычисляются юлианских дни (формула 3) и, соответственно, вычисляется изменение положения Солнца в пространстве.
JD=((min/60)/24)+hour/24+day+month_day+((year-2000)*365–0.5)+delta_day, (3)
где JD — количество юлианских дней, delta_day — значение, определяющее изменение количества дней в году, поскольку 1 год из каждых 4 лет содержит 366 дней..
L=280.461+0.9856474*JD+720 (4)
L- средняя восточная долгота Солнца;
ω= 357.528+0.9856003*JD (5)
ω- средний угол солнечной аномалии;
Le=L+1.915*sin(ω)+0.02*sin(2 ω) (6)
Le- средняя восточная долгота Солнца по эклиптике;
ɤ=23.439–0.0000004*JD (7)
ɤ- угол наклона плоскости эклиптики;
Ω- прямое восхождение- угол рассчитывается по следующей условной формуле:
y=cos(ɤ)*sin(Le), x=cos(Le);
α=arctg(y/x), eger x<0: Ω= α +180 eger y<0 we x>0: Ω = α +360;
или: Ω= α (8)
Угол наклона Солнца:
θ =asin(sin(ɤ))*sin(Le) (9)
Расстояние от Земли до Солнца рассчитывается по следующей формуле для разного времени:
r=(1.00014–0.01671*cos(ω)-0.00014*cos(2ω))*149597871; (10)
Программное моделирование
Рассчитав значения θ и r по формулам 4–10 и подставив их в формулу (2), можно вычислить силу солнечного давления, действующую на спутник. Но как видно из формул, при подстановке значений θ и r в формулу (2) образуется сложное условное уравнение. Чтобы решить это уравнение для любого заданного времени, формулы, описанные выше, были закодированы и решены на языке программирования Python.
Анализ расчетов
На рисунке 2 графически показано сравнение расчетных значений коэффициента давления (синяя линия) за 2023–2024г. и данных, полученных из спутниковой базы данных (красная линия).
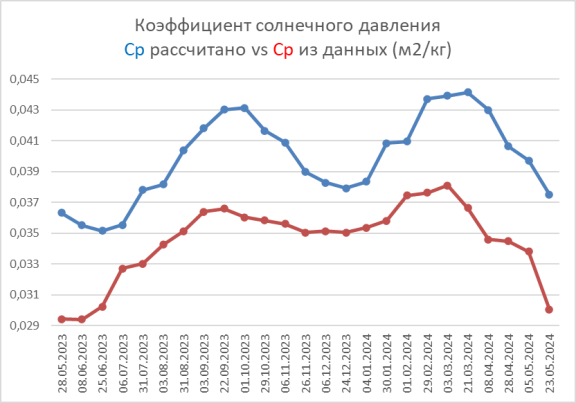
Рис. 2
На рисунке 3 графически показано сравнение расчетных значений силы солнечного давления за 2016–2017 и 2023–2024 годы.
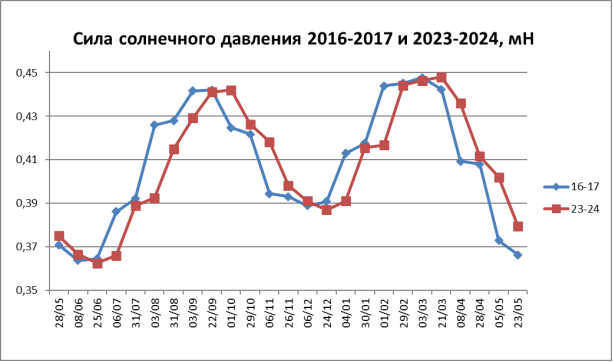
Рис. 3
На рисунке 4 графически показано сравнение расчетных значений ускорения, создаваемого силой солнечного давления на спутник за 2016–2017 и 2023–2024 годы.
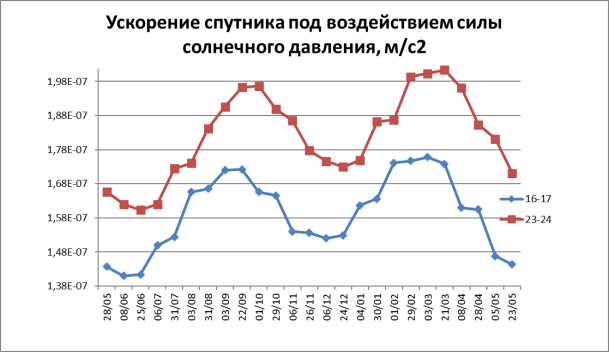
Рис. 4
На рисунке 5 показано сравнение расчетных значений расстояния, на которое сила солнечного давления может переместить спутник в свободном состоянии за одни сутки для 2016–2017 и 2023–2024 годов.
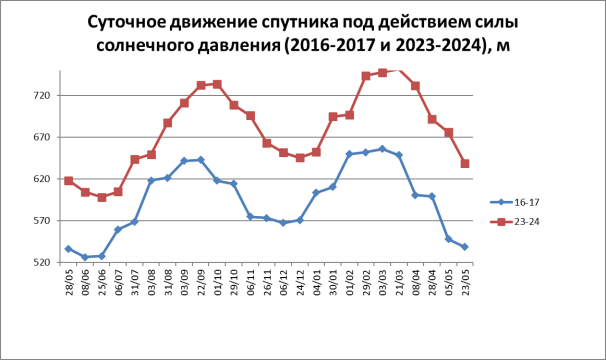
Рис. 5
Пример расчёта солнечного давления
Например, рассчитаем солнечное давление, действующее на спутник связи на дату 06/08/2016. На эту дату
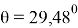
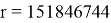
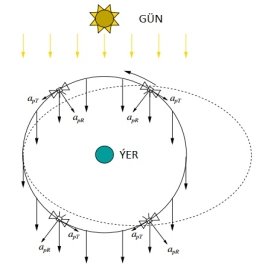
Рис. 6
Заключение
В данном исследовании были рассчитаны коэффициент солнечного давления и сила солнечного давления на спутники, движущиеся по геостационарной орбите, и сопоставлены с данными (коэффициентом давления), полученными из спутниковой базы. Согласно рисунку 3, график показывает почти одинаковые значения для разных лет. Это означает, что сила солнечного давления имеет большие изменения в течение года, которые максимальны в марте и сентябре. Однако ускорение и суточное движение спутника силой солнечного давления увеличиваются по годам. Так как масса спутника уменьшается с использованием топлива для маневров. Как видно из графиков выше (рис. 2), расчетных значений коэффициента давления и оценочные данные дают близкие значения. Это показывает, что уровень точности расчетов достаточен. Результаты также показывают, что сила солнечного давления не зависит от восточного расстояния геостационарной спутниковой орбиты, и этот эффект изменяет эксцентриситет спутниковой орбиты (рис. 6). Точный расчет силы солнечного давления очень важен для маневров, выполняемых для управления спутниками на их орбитах. Это одна из основных проблем в предоставлении бесперебойных высококачественных услуг связи клиентам спутниковой системы связи.
Литература:
- Документы по орбитальной динамике компании «Thales Alenia Space» для геостационарного спутника.— 2014.
- Gerard Maral «Satellite communications systems» — 2009.
- Astronomical Almanac — TheNauticalAlmanac.com -2024.
- Chia-Chun «George» Chao and Spencer Campbell «Estimating solar radiation pressure for geo debris» -2009.
- Hernandez, C., and R. Jehn, «Classification of Geosynchronous Objects, Issue 8,» ESOC, Darmstadt, GE, February 2006.
- Jehn, R., V.Agapov and C.Hernanadez, «The Situation in the Geosynchronous Ring,» Advances in Space Research (a COSPAR publication),JASR 7327, 26 March 2005.

