Циклическое кодирование



В статье автор рассматривает циклические коды, их построение и применение для обнаружения и исправления ошибок в передаче данных.

Ключевые слова: циклические коды, полиномы, кодирование данных, код Хэмминга, контрольные символы.

Пусть генератор циклического кода. Несистематическое кодирование полинома сообщения .

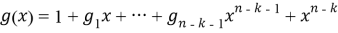
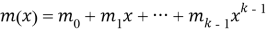
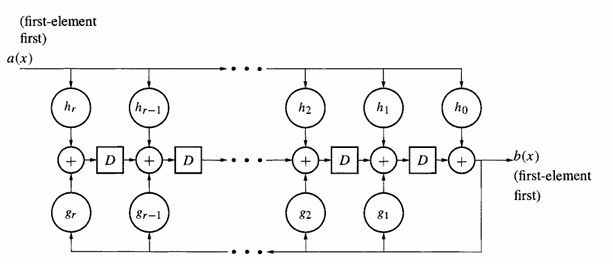
Рис. 1. Реализация (первый элемент первый), форма наблюдаемости

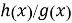
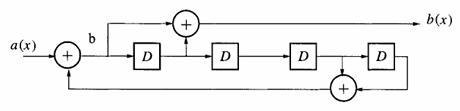
Рис. 2. Схемная реализация форма контроллера

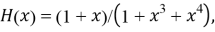
Это можно сделать, сдвинув m(x) (начиная с символа старшего порядка ) в одну из схем, перерисованных с коэффициентами g(x) на рис. 4.

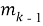
Чтобы вычислить систематическое кодирование, необходимо выполнить следующие шаги:

1. Вычислите

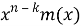
2. Разделите на и вычислите остаток,

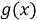
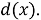
3. Вычислите

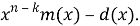
На рис. 5 показана блок-схема схемы, выполняющей эти действия. Структура подключения такая же, как у полиномиального делителя. Однако вместо того, чтобы подавать сигнал с левого конца, сигнал подается с правого конца, что соответствует сдвигу на . Затем этот сдвинутый сигнал делится структурой обратной связи.

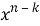
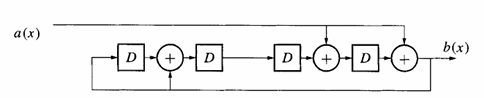
Рис. 3. Реализация схемы , форма наблюдаемости

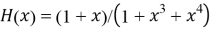
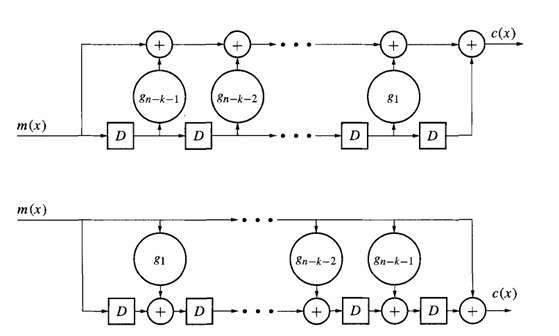
Рис. 4. Несистематическое кодирование циклических кодов

Операции выполняются следующим образом:

1. Когда ворота «открыты» (пропускают сигнал), а переключатель находится в положении A, символы сообщений подаются (в таком порядке) в систему обратной связи и одновременно в канал связи. После сдвига сообщения символы в регистре образуют остаток — это символы четности.
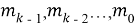
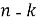
2. Затвор «закрывается», удаляя обратную связь. Переключатель переводится в положение B. (Для двоичного поля коэффициенты -1 не нужны).
3. Система тактируется раз больше, чтобы сдвинуть символы четности в канал.

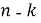
Пример 1. Для (7, 4) двоичного кода Хэмминга с генератором систематическая схема кодера показана на рис. 5. Для сообщения с полиномом содержимое регистров показано здесь.

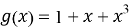
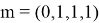
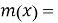
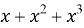
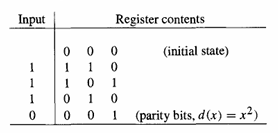
Последовательность выходных битов такова

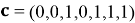
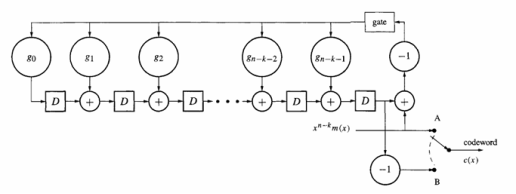
Рис. 5. Схема для систематического кодирования с использованием

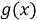
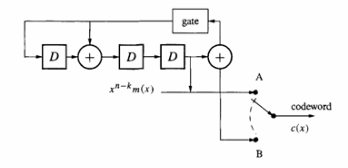
Рис. 6. Систематический кодер для кода (7, 4) с генератором

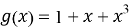
Систематическое кодирование также может быть выполнено с помощью полинома проверки на четность . Поскольку мы можем записать условие в виде

(1)

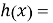
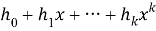
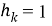
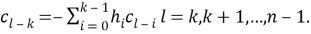
Учитывая систематическую часть сообщения биты проверки на четность могут быть найдены из (1). Схема для выполнения вычислений показана на рис. 7. Операция выполняется следующим образом.

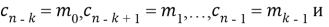
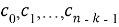
1. При открытом затворе 1 (прохождение символов сообщения) и закрытом затворе 2, а также при очищенном до 0 регистре синдрома, сообщение сдвигается одновременно в регистры и в канал, начиная с символа В конце k сдвигов регистры содержат символы , читая слева направо.

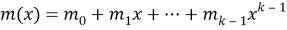
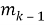
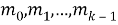
2. Затем ворота 1 закрываются, а ворота 2 открываются.

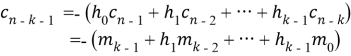
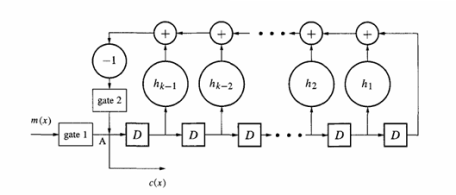
Рис. 7. Систематический кодер с использованием полинома проверки четности.

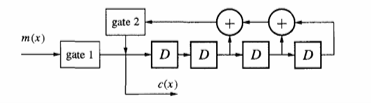
Рис. 8. Систематический кодер для кода Хэмминга с использованием

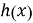
Первая цифра проверки четности производится и появляется в точке, обозначенной A. одновременно подается в канал и в буферный регистр (через затвор 2).

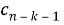
3. Вычисления продолжаются до тех пор, пока не будут получены все

символы проверки четности.

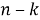
Пример 2. Для генератора кода (7, 4) полином проверки на четность имеет вид

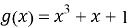
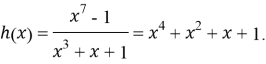
На рис. 8 показана схема систематического кодера. (Коэффициент -1 удален из-за двоичного поля.) Предположим, что . Биты (0,1,1,1) сдвинуты внутрь (причем бит 1 сдвинут первым). Тогда содержимое регистров будет выглядеть следующим образом

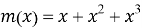
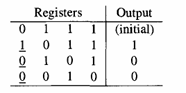
Последовательность выходных битов такова что совпадает с кодировкой из примера 1.

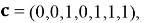
Литература:

1. Moon, Todd K. (2005). Error Correction Coding.