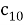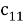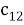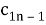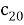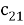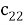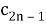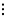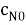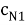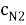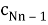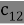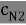В статье автор исследует подверженность данных к ошибкам во время их передачи, а также способ появления стираний, как происходит стирание и рассмотрение метода исправления ошибок.
Ключевые слова : стирание, двоичное декодирование стирания.
Стирание — это ошибка, в которой местоположение ошибки известно, а ее значение — нет. Ошибки могут возникать несколькими способами. В некоторых приемниках принятый сигнал можно проверить, не выходит ли он за допустимые пределы. Если он выходит за эти пределы, он объявляется стиранием. (Например, для сигнала BPSK, если принимаемый сигнал слишком близок к началу координат, может быть объявлено об ошибке).
Пример. Еще один способ, которым стирание может произойти при пакетной передаче, заключается в следующем.
Предположим, что последовательность кодовых слов
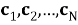
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем столбцы считываются, давая последовательность данных
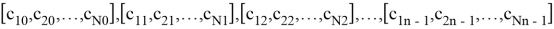
Предположим, что теперь они отправляются в виде последовательности из n пакетов данных, каждый из которых имеет длину
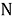
Таблица 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где серые поля обозначают потерянные данные. Хотя потерянный пакет приводит к целому столбцу потерянных данных, он представляет собой только один стертый символ кодовых слов, символ, местоположение которого известно.
Иногда стирания также могут быть объявлены с помощью техники конкатенированного кодирования, когда внешний код объявляет стирания в некоторых позициях символов, которые затем исправляются внутренним кодом.
Рассмотрим возможность стирания для кода с расстоянием
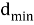
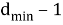
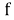
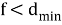
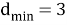
Теперь предположим, что существуют и ошибки, и стирания. Для кода с
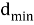
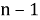
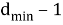
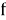
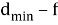
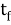
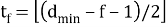
Таблица 3
|
Вставка: Протокол UDP |
|
UDP — протокол пользовательских дейтаграмм — является одним из протоколов в наборе протоколов TCP/IP. Самый распространенный протокол, TCP, обеспечивает доставку пакетов, подтверждая каждый успешно полученный пакет и повторно передавая пакеты, которые запутались или потерялись при передаче. UDP, с другой стороны, является открытым протоколом, который не гарантирует доставку пакетов. По ряду причин он имеет меньшую задержку доставки и, как следствие, представляет интерес для коммуникационных приложений, работающих в режиме, близком к реальному времени. Разработчик приложения должен бороться с потерянными пакетами, используя, например, методы коррекции ошибок. |
Если есть
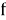
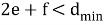
Поскольку исправление ошибки требует определения как положения ошибки, так и ее значения, в то время как заполнение стирания требует определения только значения ошибки, по существу, может быть заполнено в два раза больше стираний, чем исправлено ошибок.
Теперь мы рассмотрим, как с помощью заданного алгоритма декодирования одновременно заполнить f пробелов и исправить e ошибок в двоичном коде. В этом случае для каждой ошибки достаточно определить, каким должно быть пропущенное значение — единицей или нулем. Алгоритм декодирования ошибок для этого случая может быть описан следующим образом:
-
Поставьте нули во все стертые координаты и декодируйте, используя обычный декодер для данного кода. Назовем полученное кодовое слово
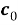
-
Поставьте единицы во все стертые координаты и декодируйте, используя обычный декодер для данного кода. Назовем полученное кодовое слово
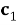
-
Найдите, какое из
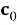
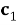
Давайте разберемся, почему этот декодер работает. Предположим, что у нас есть
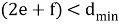
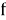
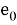
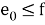
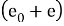
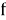
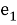
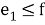
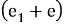
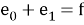
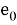
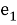
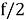
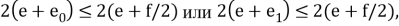
и
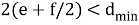
Декодирование стирания для недвоичных кодов зависит от конкретной структуры кода (например, декодирование кодов Рида-Соломона).
Литература:
- Moon, Todd K. (2005). Error Correction Coding.