В данной статье рассматриваются следующие расчеты: составление экспериментально-статистической модели на основе экспериментальных данных зависимости выхода аммиака от температуры и проверка её адекватности. Построение математической модели включает структурную и параметрическую идентификацию математической модели, которая проводится с использованием современных информационных технологий.
Ключевые слова: математическая модель, экспериментально-статистическая модель, численный метод задачи моделирования, эмпирическая модель, зависимость выхода аммиака от температуры.
Математическое описание технологического объекта на основе экспериментальных данных (эмпирическая модель) применяется в тех случаях, когда либо нет информации о механизме протекающих процессов, либо они плохо поддаются описанию с использованием физико-химических блочных моделей. В этом случае технологический объект (ТО) представляется в виде так называемого черного ящика (рис. 1) — кибернетической системы, в которой единственно доступной информацией являются её входные ( Х ) и выходные ( Y ) переменные, где X = [ x1,x2..., xn ] — вектор входных переменных, влияющих на состояние системы и её свойства, Y = [ y1,y2..., yn ] — вектор выходных переменных, характеризующих состояние системы.

Рис. 1. Изображение технологического объекта в виде «черного ящика»
Далее выявляют входные и выходные параметры процесса. К ним относятся: переменные, изменение которых связано с характером протекания процесса (управляемые переменные); переменные, изменение которых непосредственно влияет на ход процесса, — их можно измерять, а также целенаправленно изменять (управляющие воздействия); переменные, изменение которых непосредственно влияет на ход процесса, — их целенаправленное изменение невозможно (возмущающие воздействия); переменные, изменение которых косвенно связано с характером протекания процесса (промежуточные переменные). Затем определяют связи между указанными переменными и граничные условия протекания процесса.
Математическая модель процесса включает: основные переменные процесса, связи между основными переменными в статике, ограничения на процесс, критерий оптимальности, функции оптимальности, связи между основными переменными в динамике.
В данной работе будут использованы опытные данные (табл. 1):
Таблица 1
Зависимость выхода аммиака от температуры
|
Температура, град |
Выход аммиака, % |
|
723 |
35,5 |
|
748 |
31,0 |
|
773 |
26,2 |
|
873 |
23,84 |
|
973 |
7,28 |
|
1020 |
4,89 |
Применительно к рассматриваемому процессу его основным показателем является выход целевого продукта (аммиака), который зависит от ряда переменных параметров (в данном расчёте от температуры).
В общем виде эмпирические модели строятся для каждой отдельной выходной переменной из всех yi (i = 1,2,..., n) в зависимости от всех входных переменных xi (i = 1,2,..., n), т. е.
y = f (x1, x2,..., xn, α ) ,(1)
где α = [α 0, α1 ,..., α m ] — (m+1) коэффициентов эмпирической модели.
Конкретный вид функциональной зависимости ( f ) и значения коэффициентов α определяются из опытных данных, т. е. эмпирически.
Так как результаты опытных измерений являются случайными величинами, то для их обработки используется один из наиболее распространённых методов математической статистики — метод регрессионного и корреляционного анализа.
Для построения эмпирической статистической модели на выборке экспериментальных данных решаем три основные задачи:
— определяем конкретный вид функции (1), т. е. решаем задачу структурной идентификации ;
— определяем выборочные (эмпирические) коэффициенты регрессии α, т. е. решаем задачу параметрической идентификации ;
— проводим статистический (регрессионный) анализ полученных результатов с целью оценки погрешностей полученной модели.
Составление программы для построения экспериментально-статистической модели и анализ результатов моделирования
MathCad включает ряд функций для вычисления регрессии. Обычно эти функции создают кривую или поверхность определенного типа, которая минимизирует ошибку между собой и имеющимися данными.
Функции отличаются, прежде всего, типом кривой или поверхности, которую они используют, чтобы аппроксимировать данные.
Самый простой и наиболее часто используемый вид регрессии — линейная.
В программе MathCad реализована также регрессия одним полиномом, отрезками нескольких полиномов и двумерная регрессия массива данных.
Исходные экспериментальные данные:
Температура, С (аргумент)

Процент выхода аммиака, % (экспериментальные данные)
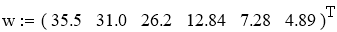
Структурная идентификация (выбор уравнения)
Для выбора уравнения с целью описания зависимости w=f(T) на основе экспериментальных данных построим график (рисунок 2)
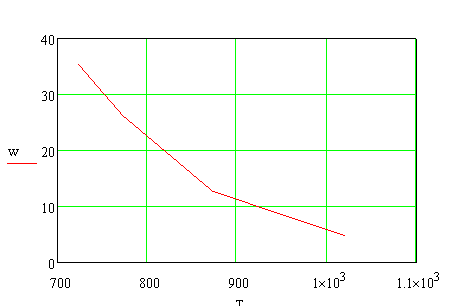
Рис. 2. График зависимости w=f(T) на основе экспериментальных данных
Видно, что зависимость w=f(T) имеет экспоненциальный характер. В соответствии с теорией зависимость выхода аммиака от температуры описывается уравнением:
w = w0*exp(-E/(R*T),(2)
где w0 — предэкспоненциальный множитель; E — энергия активации, Дж/моль; R = 8, 314 Дж/(моль*С) — универсальная газовая постоянная; T — температура, С.
Опишем экспериментальные данные с использованием этого уравнения.
Параметрическая идентификация (определение коэффициентов)
Для расчёта коэффициентов уравнения приведём его к линейному виду. Для этого проинтегрируем уравнение. В результате получим:
ln(w)=ln(w0)-E*1/(R*T),(3)
Если обозначить ye = ln(w), x = 1/T, b = ln(w0), a = -E/R, то получим линейное уравнение:
ye = b +a*x (4)
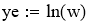
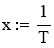
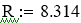
Для расчёта коэффициентов линейного уравнения воспользуемся функциями MathCad.
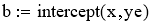
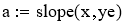
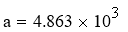
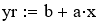
Определение значимости коэффициентов регрессии
Абсолютная величина коэффициентов значительно отличается от нуля, поэтому можно утверждать, что оба коэффициента значимы.
Анализ уравнения (4) и определение коэффициентов уравнения (2)
Построим графики по экспериментальным и расчётным значениям для линейной модели.

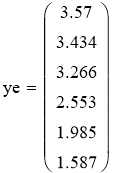
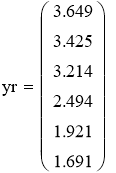
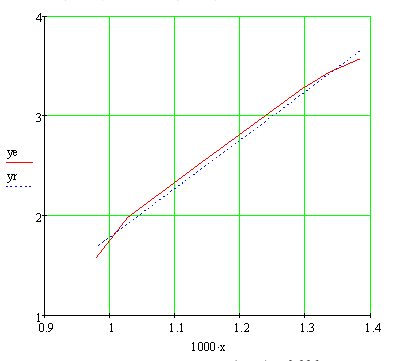
Рис. 3. График Аррениуса
Коэффициент корреляции: corr(x, ye) = 0.996
Вывод: Значение коэффициента корреляции и данные графика свидетельствуют о линейной зависимости между x и ye.
Рассчитываем коэффициенты уравнения (2):
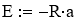
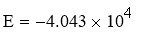
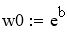
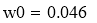
Расчётное уравнение —
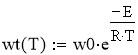
Построим графики по экспериментальным и расчётным значениям для данной модели (рис. 4).
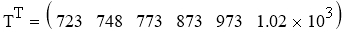


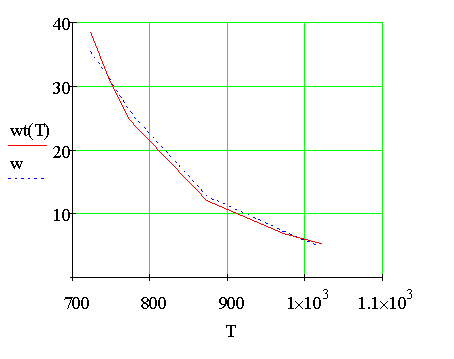
Рис. 4. Зависимость процента выхода аммиака от температуры
Проверка адекватности модели
Так как отсутствуют параллельные опыты при проведении экспериментальных исследований, то для количественной оценки адекватности модели (уравнения регрессии) необходимо определить отношение дисперсии среднего (SSср) к дисперсии адекватности (SSad) и сравнить с табличными значениями критерия Фишера.
Рассчитываем среднее экспериментальных значений процентов выхода аммиака.
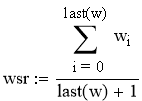
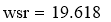
Рассчитаем дисперсию экспериментальных значений процента выхода аммиака относительно среднего значения
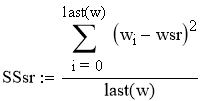
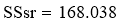
Рассчитаем дисперсию расчётных и экспериментальных значений процента выхода аммиака (дисперсию адекватности)
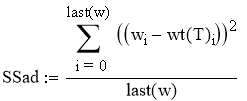
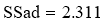
Рассчитаем критерий Фишера:
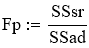
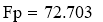
Табличное значение критерия Фишера при α=0,05; f1=1; f2=3;
Fтаб = 10,13
Так как Fp>Fтаб, модель можно считать адекватной.
Литература:
- Кафаров В. В. Методы кибернетики в химии и химической технологии: 4-е изд., перераб., доп. Учебник для вузов. — М.: Химия, 1985. — 448 с.
- Плис А. И., Сливина Н. А. MathCad 2000. Математический практикум. — М.: Финансы и статистика, 2003. — 482 с.
- Самарский А. А., Гулин А. В. Численные методы. — М.: Наука, 1989. — 432 с.

