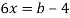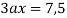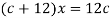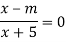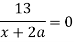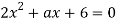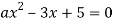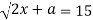Актуальность выбранной темы обуславливается существующим на сегодняшний день противоречием между необходимостью обучения учащихся решению задач с параметрами в школьном курсе математики и фактической степенью развития методики обучения этой теме на практике.
Ключевые слова: уравнение, параметр, дискриминант, квадратный трехчлен.
Задачи с параметрами часто встречались на вступительных экзаменах по математике в высшие учебные заведения. На сегодняшний день таким экзаменом является ЕГЭ по математике профильного уровня, в материалах которого регулярно встречается такая задача, но основная общеобразовательная программа по математике не упоминает в явном виде о задачах с параметрами. Тем не менее, было бы ошибкой считать, что задачи с параметром никоим образом не должны освещаться в школьном курсе математике [2, с. 14].
Как показывает анализ учебников по математике различных авторов, входящих в федеральный перечень учебников, данная тема либо затрагивается косвенно, либо выносится на самостоятельное изучение. Но, в то же время, задачи с параметрами играют важную роль в формировании логического мышления школьников и становлении их математической культуры. Необходимость развития у учащихся этих двух составляющих закреплена Федеральными государственными образовательными стандартами основного общего образования (ФГОС ООО) и среднего общего образования (ФГОС СОО). Нельзя не отметить, что важность изучения данной темы объясняется еще и тем, что навык работы с задачами с параметрами проверяется, как в Государственной итоговой аттестации 9-х и 11-х классов, так и на олимпиадах различного уровня. Этим обосновывается необходимость изучения задач с параметрами в школе.
Достаточно сложный раздел элементарной математики — решение алгебраических уравнений с параметрами — не требует для своего решения особой математической изворотливости, так как без труда проводится подготовленным школьником за 15–20 минут. При этом такая задача на ЕГЭ содержит определённую логическую сложность в выборе метода решения, что не позволяет недостаточно хорошо подготовленному ученику освоить этот раздел простым натаскиванием [1, с. 17].
При изучении алгебраических уравнений с параметрами методически правильно каждый тип уравнений (линейные, квадратные, дробно-рациональные, иррациональные) завершать задачами с параметрами. Включение таких примеров улучшает закрепление пройденного материала. Различные виды параметризации алгебраических уравнений приводятся в таблице 1.
Таблица 1
Виды параметризации алгебраических уравнений в 7–11 классах
|
Алгебраические уравнения с параметром |
Параметризация |
Примеры алгебраических уравнений |
|
Линейные уравнения |
свободного члена; |
|
|
коэффициента при переменной; |
|
|
|
свободного коэффициента и коэффициента при переменной |
|
|
|
Рациональные уравнения |
свободного члена в числителе; |
|
|
свободного члена в знаменателе; |
|
|
|
свободных членов в числителе и знаменателе; |
|
|
|
коэффициентов при переменной в числителе или в знаменателе |
|
|
|
Квадратные уравнения |
свободного члена; |
|
|
коэффициента при переменной 1-й степени; |
|
|
|
коэффициента при старшем члене; |
|
|
|
коэффициентов при переменной или свободном члене |
|
|
|
Иррациональные уравнения |
под знаком квадратного радикала; |
|
|
вне знака квадратного радикала; |
|
|
|
под знаком радикала и вне знака радикала |
|
Ниже приводятся примеры решения алгебраических уравнений с параметрами в углубленном курсе математики общеобразовательной школы.
Задача 1.
При каких значениях параметра
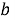
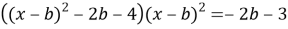
Решение. Исходное уравнение эквивалентно следующему
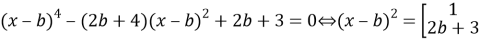
Если
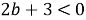
Рассмотрим теперь случай, когда
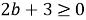
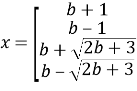
Определим, при каких значениях
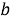



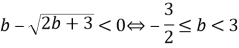
При
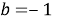

Ответ:

Задача 2.
При каких значениях параметра

|
|
(1) |
имеет не менее двух корней, больших единицы?
Решение. Разделив обе части уравнения (1) на
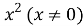
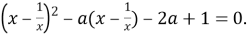
Сделав в этом уравнении подстановку
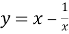
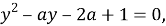
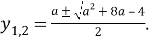
А тогда, учитывая замену, приходим к рассмотрению двух уравнений относительно
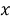
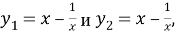
|
|
(2) |
|
|
(3) |
Замечая, что у этих уравнений свободный член отрицателен, приходим к выводу, что они обязательно имеют по одному отрицательному корню.
Таким образом, если мы найдем значения параметра

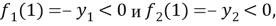
где

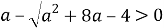

Ответ:

Задача 3.
При каких значениях
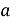
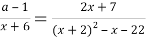
Решение. Квадратный трехчлен в знаменателе второй дроби после преобразований и разложения на простые множители примет вид:
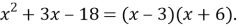
Перепишем исходное уравнение теперь в таком виде:
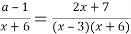
Преобразуем данное уравнение:
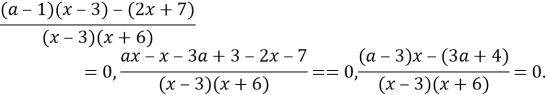
Переходим к равносильной системе
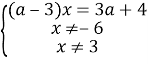
1). Если
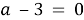
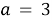
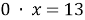
2). Если
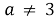

По условию задачи мы должны рассматривать лишь неположительные решения, поэтому искомые значения параметра


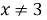
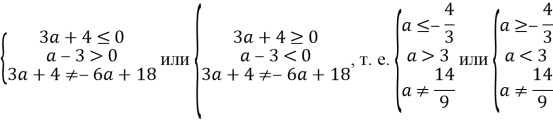
Первая система решений не имеет.
Ответ
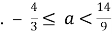

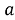
Задача 4.
Найдите все значения параметра

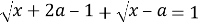
Решение. Уравнение равносильно следующей системе:
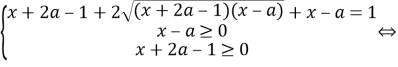
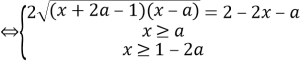
В свою очередь, полученная система равносильна системе:
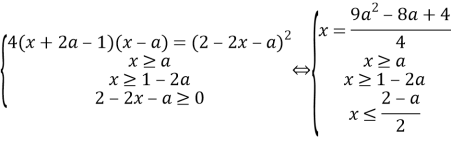
Найдём, при каких значениях параметра
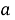
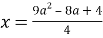
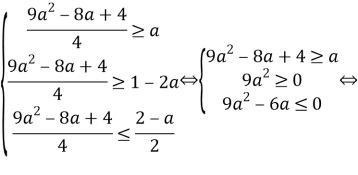
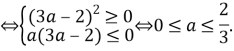
Таким образом, исходное уравнение имеет хотя бы один корень при
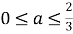
Ответ:
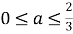
Задача 5.
Найдите все значения

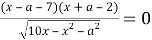
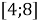
Решение. Числитель должен быть равен 0, а знаменатель не равен нулю и определён. Получаем две возможности:
A

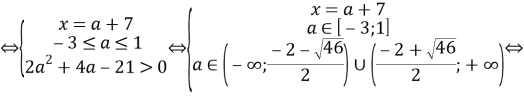
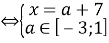
Б
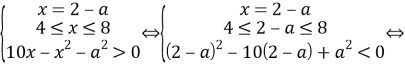
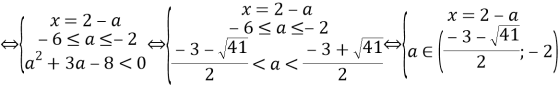
Ответ: единственное решение

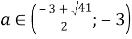
Решение
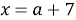
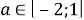
Литература:
- Малкова, А. Г. Математика. Задачи с параметрами: 12 методов решения. ЕГЭ математика 2024 / А. Г. Малкова. — Ростов-на-Дону: Изд-во «Феникс, 2024. — 392 с.
- Шестаков, С. А. ЕГЭ. Математика. Задачи с параметром. Задача 17 (профильный уровень) / С. А. Шестаков. — Москва: Изд-во МЦМНО, 2023. — 288 с.