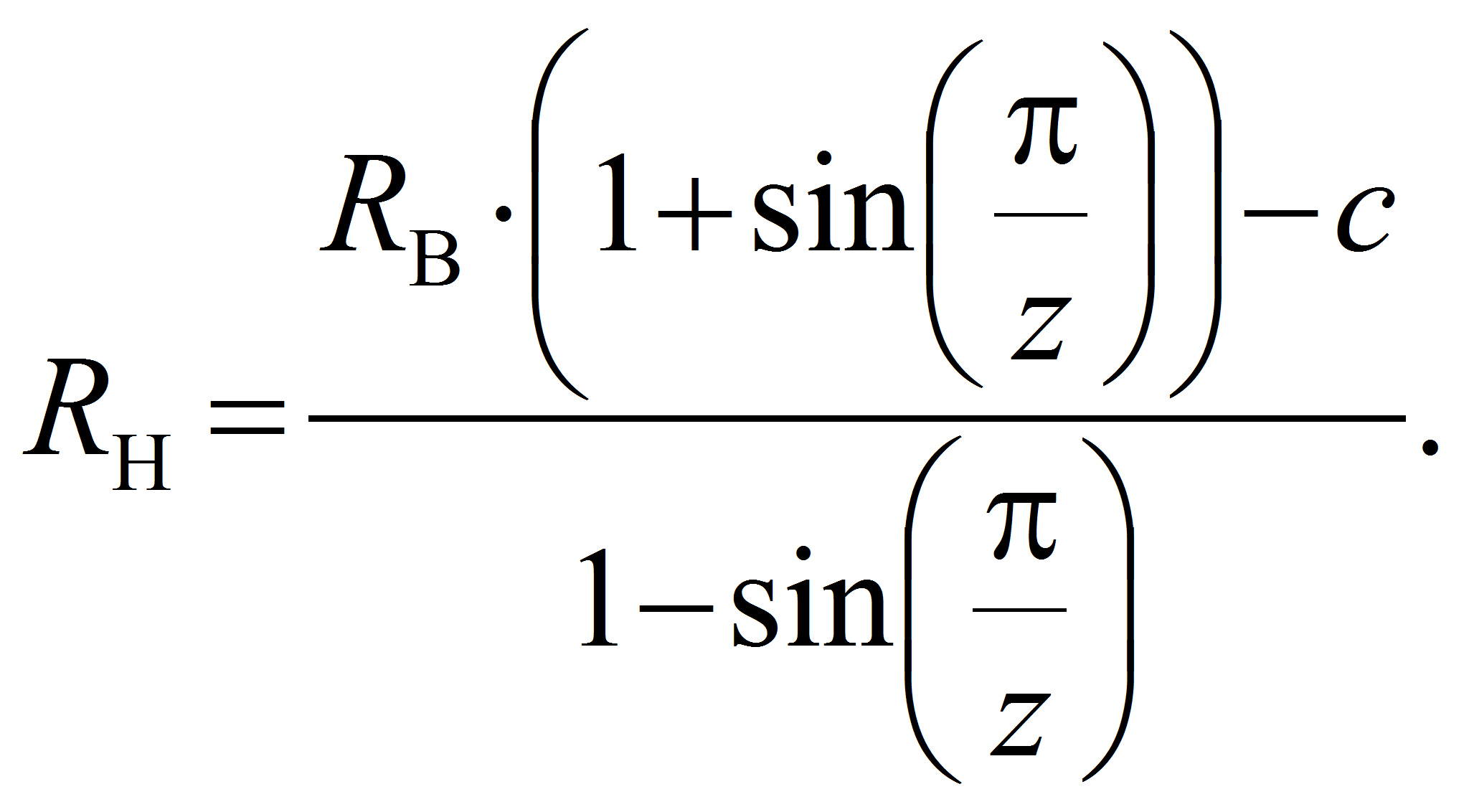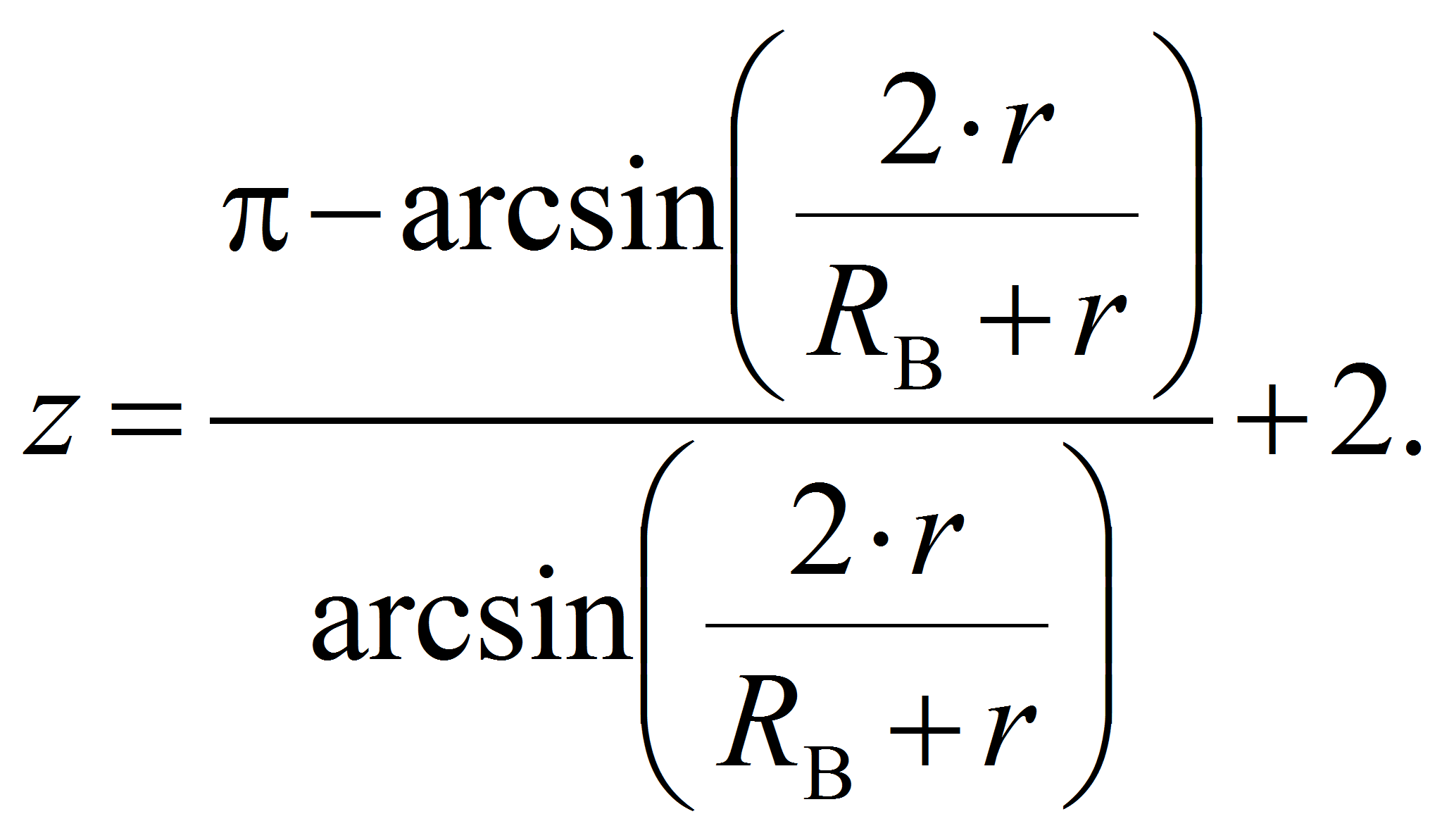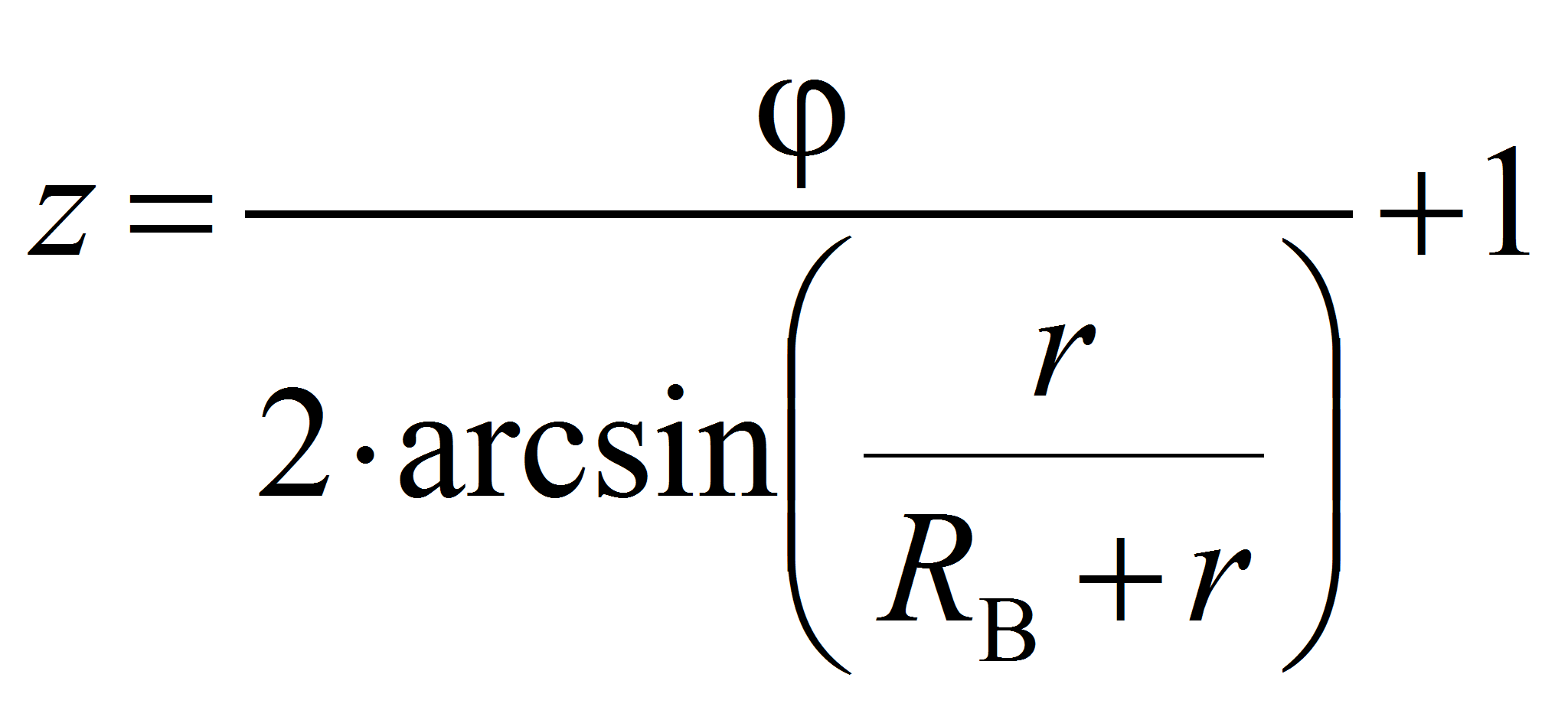Формирование областей существования механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) при вводе поправки по дорожке качения наружного кольца

Рассматривается общий случай решения задачи по формированию областей существования механизма с замкнутой системой тел качения (ЗСТК) с диаметрами равной величины являющегося механизмом-прототипом эксцентрикового механизма качения (ЭМК) с сепаратором (водило) при вводе поправки в расчет номинальных значений геометрических параметров по дорожке качения наружного кольца.

Ключевые слова: механизм с замкнутой системой тел качения с диаметрами равной величины, механизм-прототип, эксцентриковый механизм качения, тела качения, сепаратор, дорожка качения, геометрические параметры.

Форма исполнительного органа и вид движения совершаемого его выходным звеном оказывают непосредственное влияние на эффективность механизмов приводов технологического оборудования. Простота структуры механизма при минимально возможном числе подвижных звеньев совместно с реализацией сложного движения выходного звена позволяют обеспечить повышение показателей качества технологического оборудования, что возможно добиться разработкой привода на базе механизмов с замкнутой системой тел качения (ЗСТК). Механизмы данного вида могут содержать в своей структуре тела качения с диаметрами как равной, так и разной величины. Механизм с замкнутой системой тел качания с диаметрами равной величины является механизмом-прототипом для эксцентрикового механизма качения (ЭМК) как с сепаратором (водило), так и без данного звена. Для ЭМК характерно смещение центров дорожек качения колец относительно друг друга на величину эксцентриситета и наличие замкнутой системы тел качения с диаметрами разной величины [1]. Коллектив авторов проводит теоретические и экспериментальные исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования разработанного на базе механизмов данного вида с диаметрами разной (эксцентриковые) [1…3] или равной (соосные) [4…6] величины. Тела качения механизмов данного вида могут обладать или гладкими рабочими поверхностями (фрикционные) [1…8] или поверхностями с выступами (зубчатые) [9…12].

Анализ результатов выполненных исследований представленных в работах [1…8], показывает, что задача по определению номинальных значений геометрических параметров механизмов данного вида не зависимо от направления вода поправки в выполняемый расчет в некоторых случаях не имеет решения. Указанная ситуация является следствием выбора неверного сочетания величин исходных данных. Определение границ областей существования механизма с замкнутой системой тел качения с диаметрами равной величины, являющегося механизмом-прототипом ЭМК, позволит исключить сочетания исходных данных, при которых задача по определению номинальных значений геометрических параметров не имеет решения.

Рассмотрим пример решения задачи по определению границ областей существования механизмов с замкнутой системой тел качения с диаметрами равной величины с сепаратором (водило) при вводе поправки в расчет по дорожке качения наружного кольца. Для этого составим расчетную модель (рис. 1) и примем следующие исходные условия и обозначения: , — дорожки качения внутреннего и наружного колец; R_В, R_Н, О_В и O_Н — радиусы и геометрические центры дорожек качения внутреннего и наружного колец; С — сепаратор (водило); — зазор между телами качения; r₀, r₁, r_i и , , — радиусы и углы положения тел качения.

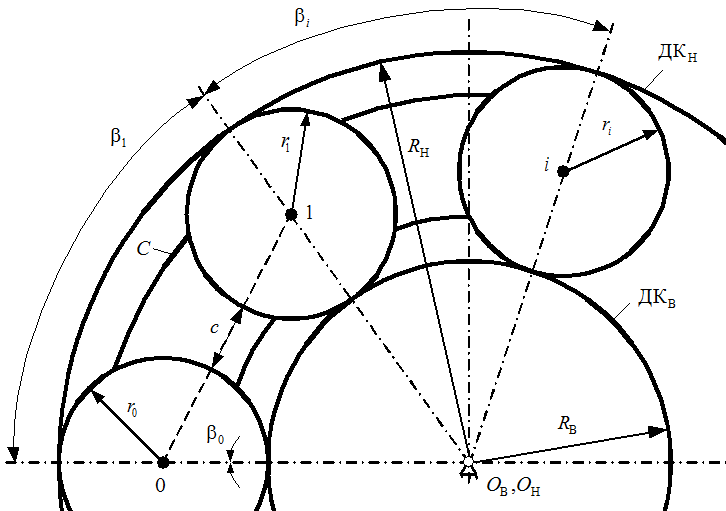
Рис. 1. Расчетная модель механизма с замкнутой системой тел качения с диаметрами равной величины с сепаратором (водило)

В работах [4…6] авторами обосновано и сформулировано условие сборки механизма с ЗСТК с диаметрами равной величины, являющегося механизмом-прототипом ЭМК, которое гласит: число тел качения (z), на угле расположения от 0 до , должно являться целым числом, а при наличии сепаратора (водило) в его структуре, должно удовлетворять условию z  2. Следуя условию сборки и проведя ряд преобразований для механизма рассматриваемого вида с сепаратором (водило), получим:

(1)

Считая, что преобразуем формулу (1) к виду

(2)

где — радиус тел качения.

Варьируя числом тел качения в интервале (0…100), проведем вычисления по выражениям (1) и (2) для величины зазора между телами качения и значений радиуса дорожки качения внутреннего кольца: 55; 65; 75; 85; 95 и 100 мм. С целью повышения эффективности выполняемых расчетов, авторами разработано программное обеспечение [13, 14], которое представляет собой совокупность программных комплексов: «Эксцентрик», «ЭПМ V1» и «ЭПМV1.01» зарегистрированных в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [15–17].

Анализ результатов полученных вычислений показывает при значениях , , , а также , , радиус тел качения равен нулю, т. е. , что соответствует структуре механизма не содержащей тела качения. Дальнейшее увеличение числа тел качения для приведенных значений радиуса дорожки качения внутреннего кольца и зазора дает отрицательные величины. Это означает, что при данных значениях механизм с замкнутой системой тел качения с диаметрами равной величины с сепаратором не существует.

Используя результаты проведенных вычислений, выполняем синтез диаграммы изменения величин радиусов дорожки качения внешнего кольца и тел качения от их количества (рис. 2). Посредством наложения функциональных кривых на одну плоскость координат получим области существования механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) при вводе поправки в расчет по дорожке качения наружного кольца. Анализ диаграммы (рис. 2) показывает наличие нескольких областей существования механизма рассматриваемого вида. С целью дальнейшего анализа нанесем на плоскость диаграммы границы данных областей.

Рис. 2. Диаграмма областей существования механизма с ЗСТК с диаметрами равной величины с сепаратором при вводе поправки по дорожке качения наружного кольца

1 — , 2 — , 3 — ,

4 — , 5 — , 6 —

Анализ результатов вычислений проведенных по выражениям (1) и (2) и диаграммы представленной на рис. 2 показывает: область А ограничена значениями 2  z  6 при 0  R_Н/r  3,08 и соответствует области существования механизма с ЗСТК с сепаратором (водило) обладающего телами качения с радиусами превышающими величину радиуса дорожки качения внутреннего кольца, т. е. . Дальнейший анализ результатов полученных по выражениям (1) и (2) указывает на существование области D ограниченной значениями z  (45…80) при R_Н/r  (29,86…51,88). Данная область соответствует области существования механизма с сепаратором (водило) и замкнутой системой тел качения в виде иголок (малые ролики), обладающих радиусами значительно меньше радиуса дорожки качения внутреннего кольца (рис. 2), а дальнейший рост числа тел качения приводит к отрицательным величинам их радиусов. Это означает, что при данных значениях механизм рассматриваемого вида не существует. В результате проведенных действий получаем область С расположенную между областями А и D и ограниченную значениями 6  z  (45…80) при 3,08 R_Н/r  (29,86…51,88), которая соответствует области существования механизма с ЗСТК и сепаратором (водило) с телами качения в виде роликов, обладающими радиусами меньше величины радиуса дорожки качения внутреннего кольца . Анализ диаграммы областей существования (рис. 2) показывает, что рост значений радиуса дорожки качения внутреннего кольца сопровождается увеличением радиуса дорожки качения наружного кольца при практически неизменных величинах радиусов тел качения в виде роликов, что также сопровождается смещением максимальной границы области С в положительном направлении оси z в интервале (45…80).

Если тела качения механизма с ЗСТК с сепаратором (водило) являются роликами, то следуя работам [4…6] число тел качения определим по выражению

(3)

Варьируя в формуле (3) значением радиуса дорожки качения внутреннего кольца в интервале (55…100) мм, проводим уточнение границ области С. Сравнительный анализ полученных значений 6  z  (61…100) при 1,24 R_Н/r  (64,75…86,88) с ранее выявленными величинами указывает на расположение максимальных границ в области D. Это означает, что вычисленные значения не могут быть приняты за границы рассматриваемой области существования механизма с замкнутой системой тел качения с сепаратором (водило), а ранее определенные границы являются действительными.

Считая, что тела качения механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) являются шариками, то следуя работам [4…6] число тел качения содержащихся в его структуре определим по выражению

, (4)

где — угол заполнения.

Варьируя значениями угла заполнения в пределах (186…200)⁰ [5, 6] и радиусом дорожки качения внутреннего кольца в интервале (55…100) мм, выполняем определение границ областей в соответствии с формулой (4), что позволяет сформировать область В, ограниченную числом тел качения 6  z  (35…61) при 3,08  R_Н/r  (15,07…64,75). Данная область соответствует области существования механизма с замкнутой системой тел качения в виде шариков, обладающими радиусами меньше радиуса дорожки качения внутреннего кольца при наличии сепаратора (водило) в его структуре, т. е. . Анализ диаграммы представленной на рис. 2 показывает: рост значений радиуса дорожки качения внутреннего кольца приводит к увеличению радиуса дорожки качения наружного кольца при незначительных изменениях радиуса тел качения в виде шариков, что сопровождается смещением максимальной границы области В в положительном направлении оси числа тел качения в интервале (35…61), а также расширением площади данной области. Сравнительный анализ областей С и D показывает, что при одних и тех же значениях исходных данных область С всегда имеет большую площадь.

В результате представленных действий определены границы областей существования механизмов с замкнутой системой тел качения равной величины с сепаратором (водило), являющегося механизмом-прототипом ЭМК при вводе поправки в расчет по дорожке качения наружного кольца. Анализ полученных областей существования показывает, что при выборе исходных данных для определения номинальных значений геометрических параметров эксцентрикового механизма качения необходимо придерживаться области В в интервале 6  z  (35…61) при 3,08  R_Н/r  (15,07…64,75) и области С в диапазоне 6  z  (45…80) при 3,08 R_Н/r  (29,86…51,88), так как при 2  z  6 и 0  R_Н/r  3,08 тела качения имеют радиусы превышающие величину радиуса дорожки качения внутреннего кольца, а при z  (45…80) и R_Н/r  (29,86…51,88) тела качения являются иголками (малые ролики) при достаточно большом их количестве, а дальнейший рост числа тел качения приводит к отрицательным величинам их радиусов. Это означает, что при данных значениях механизм с ЗСТК с диаметрами равной величины с сепаратором не существует, а указанные пределы отношения R_Н/r однозначно ограничивают значения радиуса тела качения равными не менее 2 мм, т. е. r  2. Данные рекомендации позволяют исключить сочетания исходных данных, при которых задача по определению номинальных значений геометрических параметров механизма с замкнутой системой тел качения с сепаратором (водило) не имеет решений.

Литература:

1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02. Красноярск, 2002. 26 с.

2. Мерко М. А., Меснянкин М. В., Шемякин Д. В., Леонтьев А. С., Собко И. В. Особенности формирования математической модели ЭМК при ведущем наружном кольце // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/mn2011/thesis/s19/ Shemyakin.pdf.

3. Меснянкин М. В., Мерко М. А., Колотов А. В., Беляков Е. В., Белякова С. А. Математическая модель ЭМК с сепаратором при ведущем внутреннем кольце // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 62–67.

4. Мерко М. А., Меснянкин М. В, Беляков Е. В., Колотов А. В., Груздев Д. Е. Определение областей существования прототипа эксцентрикового механизма качения // Механики ХХI веку: сборник докладов VII-ой Всероссийская науч.-тенх. конф. с междунар. участием. Братск: БрГУ. 2008. С. 89–93.

5. Мерко М. А., Меснянкин М. В., Шевченко Е. С, Китура А. С. Формирование границ областей существования механизмов-прототипов ЭМК // Молодежь и наука: сборник материалов VIII Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых, посвященной 155-летию со дня рождения К. Э. Циолковского [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. федер. ун-т, 2012. — Режим доступа: http://conf.sfu-kras.ru/sites/mn2012/thesis/s017/s017–091.pdf.

6. Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е. Определение границ областей существования механизмов-прототипов ЭМК при вводе поправки в расчет по дорожке качения внутреннего кольца // Вестник Красноярского государственного аграрного университета. 2012. № 12. С. 138–141.

7. Мерко М. А., Меснянкин М. В., Митяев А. Е. Описание математической модели механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце // Молодой ученый. 2013. № 3 С. 71–75.

8. Мерко М. А., Меснянкин М. В., Митяев А. Е., Колотов А. В. Анализ взаимозависимостей геометрических параметров эксцентрикового механизма качения // Вестник Красноярского государственного аграрного университета. 2012. № 11. С. 180–184.

9. Беляков Е. В., Меснянкин М. В, Мерко М. А., Колотов А. В., Груздев Д. Е. Эксцентриковый планетарный механизм // Механики ХХI веку: сборник докладов VII-ой Всероссийская науч.-тенх. конф. с междунар. участием. Братск: БрГУ. 2008. С. 87–89.

10. Беляков Е. В., Колотов А. В., Меснянкин М. В, Мерко М. А. Зубчатый планетарный механизм для воспроизведения требуемого сложного закона движения выходного звена // Проблемы механики современных машин: материалы V-ой международной конференции. Улан-Удэ: ВСГУТУ. 2012. Т.1 С. 3–6.

11. Беляков Е. В., Мерко М. А., Колотов А. В., Меснянкин М. В., Митяев А. Е. Обеспечение требуемого движения выходного звена эксцентрикового эпициклического механизма // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 47–51.

12. Белякова С. А., Груздев Д. Е., Беляков А. Н., Мерко М. А., Меснянкин М. В., Колотов А. В. Применение дифференциального механизма для шлифования плоских поверхностей // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 51–56.

13. Мерко М. А., Меснянкин М. В., Файзиев А. Н., Вацлавский Е. С. Повешение эффективности проектирования эксцентриковых механизмов приводов технологического оборудования на основе ЭМК // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/ mn2011/thesis/s19/Faiziev.pdf

14. Беляков Е. В., Колотов А. В., Мерко М. А., Меснянкин М. В. Применение САПР при исследовании эксцентрикового планетарного механизма // Современные технологии. Системный анализ. Моделирование. 2012. № 3. С. 109–112.

15. Свидетельство о государственной регистрации программы для ЭВМ № 2012614197. Программный комплекс «Эксцентрик» / Меснянкин А. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Беляков Е. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612100 от 22.03.12; зарегистрировано в Реестре программ для ЭВМ 12.05.12.

16. Свидетельство о государственной регистрации программы для ЭВМ № 2012614355. Программный комплекс «ЭПМ V1» / Беляков Е. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Меснянкин А. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612237 от 27.03.12; зарегистрировано в Реестре программ для ЭВМ 16.05.12.

17. Свидетельство о государственной регистрации программы для ЭВМ № 2013610142. Программный комплекс «ЭПМV1.01» / Беляков Е. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Меснянкин А. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012660154 от 23.11.12; зарегистрировано в Реестре программ для ЭВМ 09.01.13.