В статье автор рассматривает два метода экспертных оценок — последовательные и парные сравнения и классический метод Дельфи, и в заключении делает вывод о том, какой из методов является более предпочтительным.
Ключевые слова: сравнения, методы, оценки.
Экспертные оценки играют важную роль в принятии решений в различных сферах жизни. Они позволяют учесть мнение специалистов и получить наиболее точные результаты.
Метод последовательных и парных сравнений
Последовательные и парные сравнения — это методы, основанные на сравнении объектов или альтернатив между собой. Они позволяют получить количественные оценки на основе мнений экспертов. При использовании этих методов эксперты сравнивают каждую пару объектов и дают оценку, которая отражает их предпочтение.
Метод парных сравнений основан на использовании эксперта, который оценивает цели:
Z1, Z2, …, Zn.
Для каждой пары целей эксперт определяет наиболее предпочтительную цель и выражает свое предпочтение с помощью оценки по определенной шкале. На основе полученных оценок формируется матрица, анализ которой позволяет определить веса целей, показывающие их относительную значимость. Также существует вариант метода, который включает составление матрицы бинарных предпочтений, где предпочтения целей выражаются с помощью логических переменных. Затем определяются цены каждой цели путем сложения логических переменных в соответствующей строке матрицы.
Пример 1: Эксперт оценивает 4 цели, связанные с выбором места для нового магазина. Место должно быть удалено от центра города, но рядом с аналогичными магазинами конкурентов, а также учитывать арендную плату и другие факторы. Эксперт оценивает каждый из районов, используя данные исследований. Вектор целей выглядит следующим образом:
Z1 — открыть магазин в районе A;
Z2 — открыть магазин в районе B;
Z3 — открыть магазин в районе C;
Z4 — открыть магазин в районе D.
Матрица бинарных предпочтений выглядит следующим образом в таблице 1:
Таблица 1
Матрица бинарных предпочтений
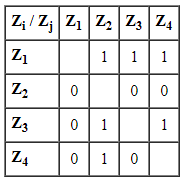
Производим построчное суммирование и определяем цены каждой альтернативы:
C1=3; C2=0; C3=2; C4=1
Нормируем полученные веса и получаем:
V1=3/6=0,5; V2=0; V3=0,33; V4=0,17
Получаем порядок предпочтения целей: Z1, Z3, Z4, Z2
Классический метод экспертных оценок Дельфи
Дельфи — это метод экспертных оценок, разработанный в 1950-х годах в США. Он основан на проведении серии анонимных опросов экспертов с целью получения согласованных мнений. Каждый эксперт оценивает каждую альтернативу, и на основе этих оценок формируется общий рейтинг. Затем эксперты знакомятся с результатами и могут изменить свои оценки, если они считают, что они были ошибочными. Этот процесс повторяется до тех пор, пока не будет достигнут консенсус среди экспертов.
Методы принятия решений Дельфи могут показаться сложными на первый взгляд, но пример использования техники Дельфи может помочь развеять эти заблуждения. Допустим, Петров хочет узнать свои шансы стать руководителем компании или получить повышение.
Он собирает команду консультантов из разных областей, таких как экономисты, инженеры, специалисты по кадрам, менеджеры по продажам, тренеры и психологи. После получения первых опросников с поставленной задачей, участники оценивают шансы Петрова по 100-балльной шкале. Если ответы сильно различаются, аналитики составляют расширенную анкету с дополнительными вопросами для второго этапа. Эксперты, дополнив данные о Петрове, его возможных и реальных конкурентах, их характеристиках, снова оценивают баллы. Проще говоря, команда экспертов генерирует идеи с помощью не только анкет, но и таких методов, как “мозговой штурм”.
После обработки аналитики выбирают наиболее эффективные идеи. В результате, разница в ответах экспертов сводится к минимуму, и инициаторы могут рассчитать среднее арифметическое из них.
Оба метода имеют свои преимущества и недостатки. Последовательные и парные сравнения просты в использовании и позволяют получить количественные результаты, но они могут быть подвержены субъективным оценкам экспертов. Метод Дельфи более точен, так как он позволяет учитывать мнения всех экспертов, но он требует больше времени и ресурсов для проведения.
Таким образом, выбор метода экспертных оценок зависит от конкретной задачи и требований к результатам. Последовательные и парные сравнения могут быть использованы для быстрого получения качественных оценок, а метод Дельфи — для получения более точных и согласованных результатов.
Литература:
1. Бражко Е. И., Серебрякова Г. В., Смирнов Э. А. Управленческие решения: Учебное пособие. — М.: РИОР, 2006. — 126с.
2. Соколова Л. Е. Разработка управленческого решения: Конспект лекций. — М.: 2008. — 188с.
3. Ивасенко А. Г. Разработка управленческих решений: Учебное пособие/ А. Г. Ивасенко, Я. И. Никонова, Е. Н. Плотникова. — Новосибирск: СГГА, 2007. -162с.

