В работе (1) доказывается однозначная разрешимость и непрерывная зависимость решений следующей задачи:
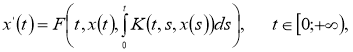
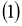
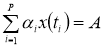
В этой работе рассматривается задача:
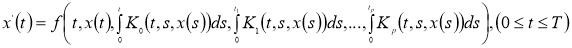
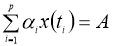
Находятся достаточные условия однозначной разрешимости и непрерывная зависимость решений от параметров, где

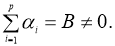
Уравнение (1) является частным случаем уравнения (2). Действительно, если
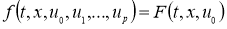
1. Однозначная разрешимость
Теорема 1.
Пусть функции
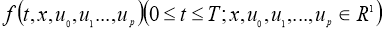
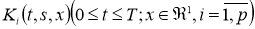
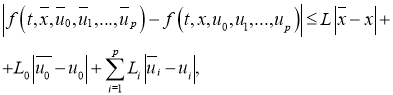
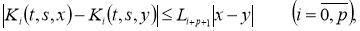
где
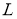
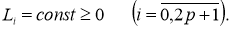
Если существует
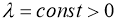
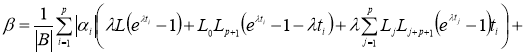
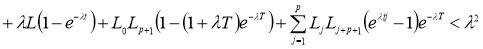
то задача (2), (3) имеет единственное решение в пространстве
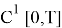
Доказательство. Очевидно, что задача (2), (3) эквивалентна интегрофункциональному уравнению:
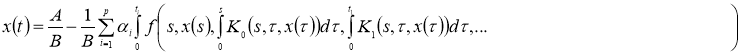
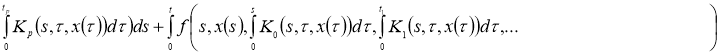
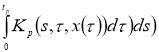
Правую часть этого интегрофункционального уравнения обозначим через оператор
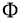
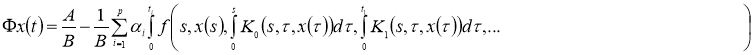
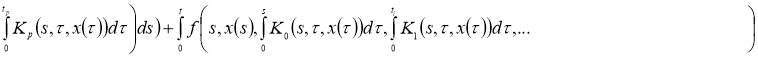
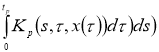
Очевидно, что
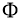
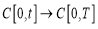
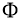
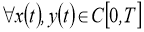
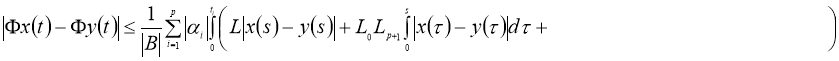
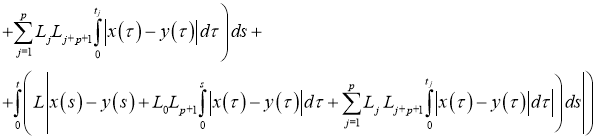
Используя
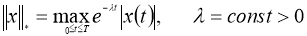
норму получим:
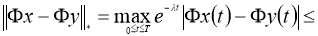
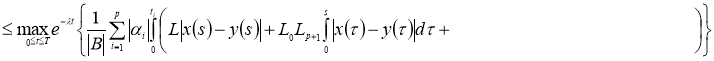
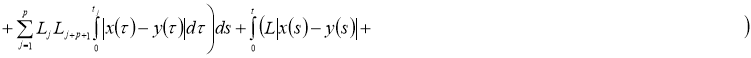
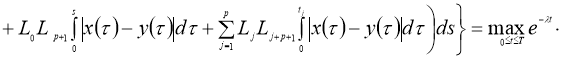
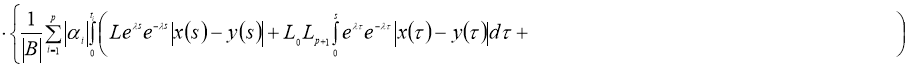
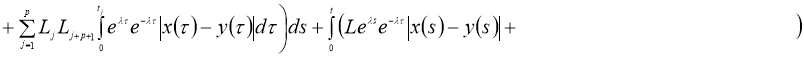
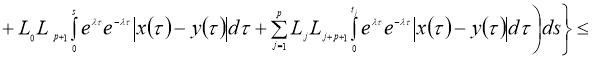
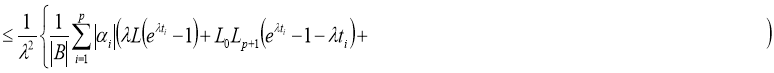
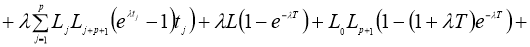
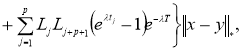
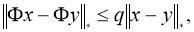
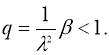
Доказательство теоремы следует из принципа сжимающих операторов.
- Непрерывная зависимость решений от параметров
Теперь рассмотрим задачу:
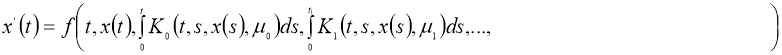
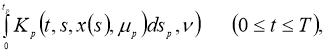
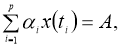
где
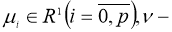
Теорема 2.
Пусть, функции
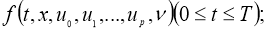
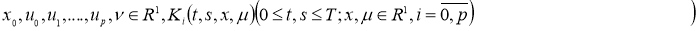

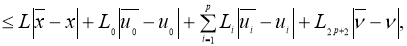
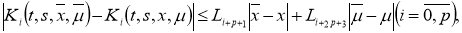
где
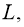
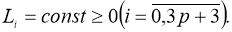
Если существует
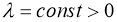
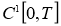
Доказательство. Задача (6)-(7) эквивалентно интегрофункциональному уравнению.
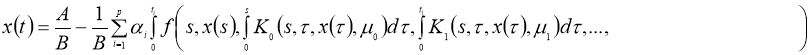
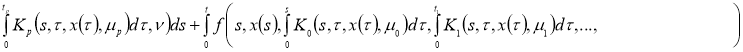
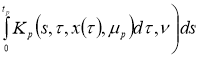
При фиксированных
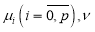
Для доказательства теоремы 2 достаточно доказать непрерывную зависимость решений от параметров.
Обозначим через
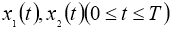
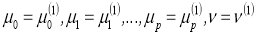
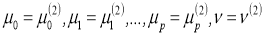
т. е.
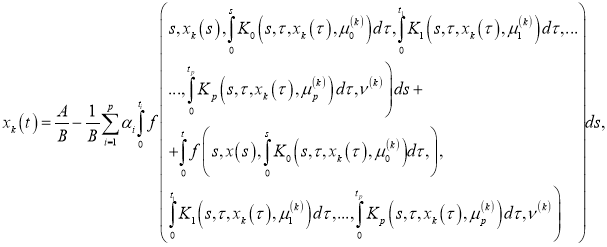
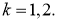
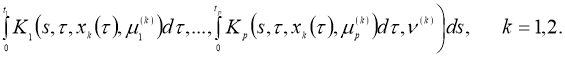
Используя условия (8), (9) из уравнения (11), имеем


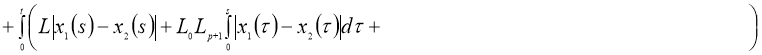
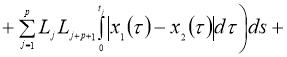
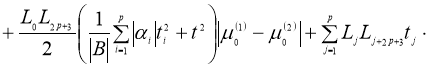
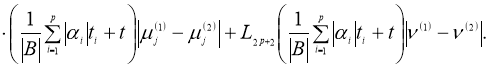
Используя норму (5), получим:
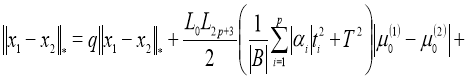


Отсюда следует утверждение теоремы 2.
Литература:
- Gurbanmämmedow N. Birinji tertipli integrodifferensial deňleme üçin köpnokatly meseläniň ýeke-täk çözüwiniň barlygy //Beýik Galkynyş eýýamynyň batly gadamlary 2011–1. Aşgabat-2011.







