In this article, the stability against overturning of the 4-axle universal semi-wagon of the 12–9922 model and the 4-axle closed wagon of the 11–9923 model manufactured in Uzbekistan was analyzed when moving on curved sections of different radii. The analysis was carried out taking into account the dynamic forces acting during the movement of an empty wagon on curved sections. According to the accounts, the information was obtained for the safe passage of the wagon through various curved sections.
Keywords: wagon technical characteristics, curvature, stability coefficient, overturning of the wagon out of curvature, inertial forces, KMZ ShK.
The railway track consists of alternating straight and curved sections. Centrifugal force acts on the car when it moves on the curved sections of the road. Centrifugal force, combined with the force of wind pressure and transverse inertial forces caused by the lateral vibration of the body, cause inconvenience to the transported load. The vibration of the body creates a moment in the springs, as a result, the car moves out of the curve, and the relatively less loaded wheel moves into the curve.
In curved sections with a radius of R, the outer rail is laid higher than the inner rail to compensate for the effect of centrifugal force. The maximum permissible height of the outer rail on a curved section is 150 mm.
Literature review
The height h of the outer rail is usually determined by the condition that the vertical loads of both wheels are the same at the head of the rail. So,
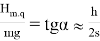
where:
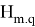
m — wagon mass,
2s — track width,
α is the elevation angle of the rail.
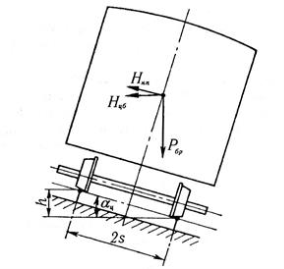
Fig. 1. Forces acting on rolling stock when moving along a curve
The stability of the wagon against overturning is estimated by calculating the conditional criterion based on the ratio of the forces of interaction of the wheels with the rails during its design.
To check the condition of the stability of the car against the overturning of the car, it is necessary to determine the centrifugal force and the stability coefficient of the car. The calculation is performed for the wagon in an empty position, because an empty wagon is less stable.
Analysis
A general algorithm for calculating the coefficient of stability with respect to external curvature.
The centrifugal force directed to the car body in an empty state is determined by the following formula.
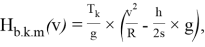
where: v = 15....33 — speed of movement of the wagon, m/s
h = height of the outer rail at a curve of 0.15, meter
Determining the force of wind pressure acting on the body, N.
Determining the point of equally acting wind pressure force and centrifugal loads at the same height from the rail head for the empty state, meter
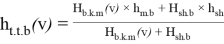
where:
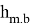
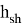
We determine the force of wind pressure on the hull
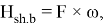
where: F is the size of the side projection of the body, m 2 ;
Determining the ratio of side forces to the weight of the body for the empty state
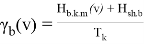
Determining the transverse displacement of the center of mass of the car under the influence of side forces for the empty state
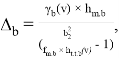
where:
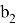
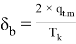
where: r = 0.478 radius of the wagon wheel
Determining the coefficient of stability of the wagon against overturning when moving along a curve
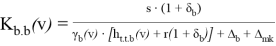
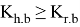
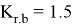
Discussion
The calculation is for closed wagons and specialized semi-wagons of model 11–9923. Specifications are listed in Table 1.
Table 1
Technical characteristics of the wagon
|
Indicators |
4-axle universal semi-wagon model |
12–9922 4-axle closed wagon model 11–9923 |
|
Carrying capacity. t |
70 |
65 |
|
Tara, t |
23.5 |
28.5 |
|
Body size m 2 |
92 |
158 |
|
Wagon base m |
8.65 |
14.14 |
The results of stability coefficient calculation are presented in Tables 2–3.
Table 2
Calculation results of the 4-axle universal semi-wagon model 12–9922
|
Curvature radius R, m |
Outer rail height h, mm |
Maximum speed V, m/s |
Calculated stability coefficient of the wagon |
Speed limit V, m/s |
|
250 |
150 |
33 |
1.203 |
28 |
|
300 |
150 |
33 |
1,337 |
29 |
|
350 |
150 |
33 |
1,363 |
31 |
|
400 |
150 |
33 |
1,374 |
33 |
|
450 |
120 |
33 |
1,470 |
33 |
|
500 |
90 |
33 |
1,543 |
33 |
|
600 |
30 |
33 |
1,628 |
33 |
|
800 |
0 |
33 |
1,890 |
33 |
|
1000 |
0 |
33 |
2.170 |
33 |
Table 3
Calculation results of 4-axle closed wagon model 11–9923
|
Curvature radius R, m |
Outer rail height h, mm |
Maximum speed V, m/s |
Calculated stability coefficient of the wagon |
Speed limit V, m/s |
|
250 |
150 |
33 |
1.148 |
26 |
|
300 |
150 |
33 |
1,180 |
28 |
|
350 |
150 |
33 |
1,195 |
30 |
|
400 |
150 |
33 |
1,329 |
30 |
|
450 |
120 |
33 |
1,267 |
32 |
|
500 |
90 |
33 |
1,260 |
33 |
|
600 |
30 |
33 |
1,281 |
33 |
|
800 |
0 |
33 |
1,494 |
33 |
|
1000 |
0 |
33 |
1,671 |
33 |
After analyzing the research, it can be concluded that the maximum permissible height of the outer rail is required for wagons of the 12–9922 and 11–9923 models in small radii (250÷400), because the rolling stock moving at a relatively low height is overturned; can go In addition, it is necessary to follow the established speed limit for safe movement.
Conclusion
For a universal semi-car of model 12–9922 with a curvature of R=250 m and a maximum height, the speed should be limited to 28 m/s, and for a closed car of model 11–9923, the speed should be limited to 26 m/s. At a curve of R=300 m, the speed is up to 29 m/s for a universal semi-wagon model 12–9922, speed limit is up to 28 m/s for a closed wagon model 11- 9923, R=350 m and height h=150 mm for the universal semi-car of the 12–9922 model, the speed of movement should be limited to 31 m/s, and for the closed car of the 11–9923 model, the speed should be limited to 30 m/s. For a universal semi-car of the 12–9922 model with a curve of R=400 m and a maximum height, the speed should be limited to 33 m/s, and for a closed car of the 11–9923 model, the speed should be limited to 30 m/s.
With the further increase of the radius (450÷1000), the height of the outer rail does not limit the speed of movement of the rolling stock, and the possibility of overturning the wagon decreases. The optimal value of the height of the outer rail for R=450 curvature is h=120 mm, for R=500 curvature h=90 mm, for R=600 curvature h=30 mm, for R=800, R=1000 the height of the outer rail is not required.
References:
- Vershinsky, C. B. Car dynamics / C. B. Vershinsky, V. N. Danilov, V. D. Khusids. -M.: Transport, 1991. — 360 p.
- Norms for the calculation and design of new and modernized cars of railways of the Ministry of Railways of the 1520 mm gauge (non-self-propelled). — M.: GosNIIV-VNIIZhT, 2005. — 317 p.
- Determining the stability of the cement-carrying wagon-hopper against overturning / H. A. Rahmatov, F. F. Muzaffarov, S. B. Namozov [et al.] // Molodoy uchenyy. — 2022. — No. 1(396). — Pp. 312–317.
- Raximov R. V. Introduction of modern technologies in the enterprise SJSRC “O’zbekiston temir yo’llari” / R. V. Raximov, F. S. Galimova // Bulletin of Tashkent State Technical University. — 2015. — No 3. — P. 159–164.
- Waail M. L. Investigated the strength of rolling stock as a fuzzy function / M. L. Waail, R. V. Rahimov // ToshTYMI Axboroti. — 2019. — № 3. — P. 43–49.
- Zaynitdinov O. I. Development of new polymer composite materials for the flooring of rail carriage / O. I. Zaynitdinov, R. V. Rahimov, M. L. Waail, Ya.O. Ruzmetov // International Journal of Engineering and Technology. — 2020. — Vol. 9. — No 2. — P. 378–381.
- Boronenko Yu.P. Experimental determination of forces through measurements of strains in the side frame of the bogie / Yu.P. Boronenko, R. V. Rahimov // Transport problems. — 2021. — Vol. 16 — Iss. 3. — P. 199–211.

