Цель работы — проанализировать значение погрешности кинематического указателя числа Маха в кабине пилота, а также рассмотреть пригодность применения пакетных программ SOLID WORKS в изучении и численном анализе аэродинамических характеристик самолета.
В статье описывается теоретический минимум для понимания определения числа Маха с помощью кинематического указателя. Рассматривается зависимость погрешностей от скоростей, высот и зависимостей окружающей среды, и прикладывается расчетный анализ характеристик.
Число Маха
Число Маха используется для характеристики скорости движения объекта в среде. Оно определяет, насколько быстро движется объект в отношении скорости распространения звуковых волн в данной среде. Для различных объектов и сред число Маха имеет разное значение и может быть как меньше единицы (движение объекта со скоростью меньше скорости звука), так и больше единицы (движение объекта со скоростью больше скорости звука). Знание числа Маха позволяет рассчитывать аэродинамические свойства объекта, такие как сопротивление воздуха, эффективность топлива. Все эти характеристики необходимы пилоту для определения эффективного полета и контроля над самолетом.
Формула числа Маха выглядит следующим образом:
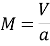
где M — число Маха, V — скорость тела, a — скорость звука в среде, в которой движется тело.
Таким образом число М учитывает в себе скорость движения и изменение параметров воздушной среды через скорость звука, которая как раз от этих параметров и зависит.
Кинематический указатель числа Маха: устройство и методы измерения
Понимая основы определения числа Маха, рассмотрим внутреннее оснащение кинематического указателя.
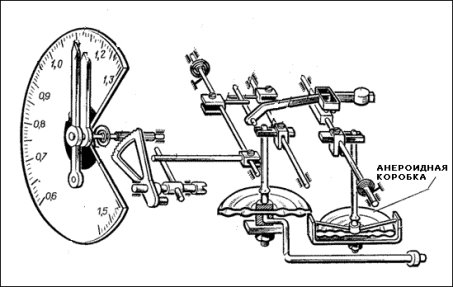
Рис. 1. Кинематический указатель
Воздух, набегая на летательный аппарат, в результате своего движения обладает некоторой кинетической энергией или, попросту говоря, скоростным напором (
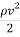
Попадая в приемник воздушного давления (ПВД, или Трубку Пито) он тормозится, и его напор превращается в давление на мембрану стрелочного прибора-указателя. Чем быстрее летит самолет, тем больше скоростной напор, тем большую скорость показывает стрелка прибора.
Воздух взаимодействует с аэродинамическими поверхностями самолета, определяя тем самым параметры его полета. А эти параметры зависят от параметров состояния воздуха, как газа, которые, конечно, зависят от условий, в которых находится данный объем газа.
Трубка Пито выглядит так.
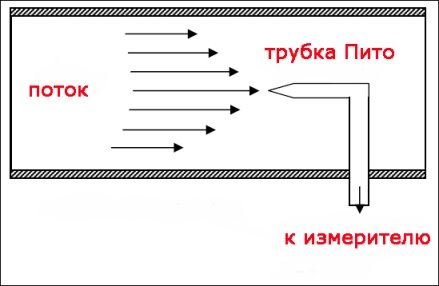
Рис. 2. Трубка Пито
Для расчета скорости применяется следующая формула:
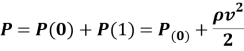
Полное давление Р, динамическое — Р1, статическое — Р0, скорость полета (потока) — V, плотность воздуха ρ.
Выражаем нужное нам
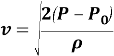
Благодаря выводу этих формул, можно начинать подготовку к опытам.
Сравнение характеристик
Для сравнения я буду использовать практические характеристики, которые я взял из данных полета самолета Boeing 747–800 по датчику числа Маха, расчетное число маха, которое буду выводить через вышеупомянутые формулы, и результаты, предлагаемые программными комплексами Solid Works.

Рис. 3. Модель самолета Boeing 747–800
Создаю гибридную сетку расчета и устанавливаю примерное количество ячеек в 5800000. Датчик скорости, как и в реальной модели расположения трубки Пито, ставлю в носовой части.
Таблица 1
Сравнение скорости звука в км/ч
|
Высота, м |
Практические данные, км/ч |
Расчетные данные, км/ч |
Solid Works , км/ч |
|
0 |
1 225,2 |
1 223,54 |
1 227,1 |
|
1000 |
1 211,7 |
1 210,4 |
1 213,2 |
|
3000 |
1 183,7 |
1 184 |
1 184,4 |
|
5000 |
1 154,2 |
1 149,9 |
1 153,1 |
|
7000 |
1 124 |
1 124,7 |
1 125,1 |
|
9000 |
1 094,3 |
1 094,2 |
1 093,6 |
|
11000 |
1 062,4 |
1 062,3 |
1 060,43 |
Далее можно произвести подсчеты и вычислить погрешность.
Таблица 2
Сравнение погрешности скорости звука в процентах
|
Высота, м |
Погрешность расчетных относительно практических |
Погрешность программных относительно практических |
|
0 |
0,0013 |
0,0015 |
|
1000 |
0,0010 |
0,0253 |
|
3000 |
0,0002 |
0,0005 |
|
5000 |
0,0037 |
0,0021 |
|
7000 |
0,0006 |
0,0011 |
|
9000 |
0,0001 |
0,0010 |
|
11000 |
0,0001 |
0,0024 |
Сравнив скорость звука, понимаем, что погрешность для использования программных комплексов отличается, но не больше, чем 2 единицы второго числа после запятой, в этом случае погрешность можно считать допустимую при расчетах аэродинамических аппаратов гражданской авиации.
Далее запускаем расчет с формулами, где укажем определение числа Маха и посмотрим сравнительно на показания датчика Маха во время полета и рассчитаем реальное число маха.
Таблица 3
Сравнение числа Маха
|
Высота, м |
Показания кинематического указателя |
Показания расчетного реального |
Погрешность, % |
|
0 |
0,41 |
0,361 |
0,119 |
|
3000 |
0,56 |
0,502 |
0,103 |
|
5000 |
0,68 |
0,601 |
0,116 |
|
9000 |
0,79 |
0,753 |
0,046 |
Как видно из таблицы, погрешность существует, количественно больше, нежели погрешность скорости звука из прошлого расчета. Кинематический указатель указывает показание всегда больше, и ошибается на 1–2 деления по шкале прибора.
Таким образом, анализ показал большую погрешность при определении числа Маха кинематическим указателем. Доказана эффективность применения программных комплексов, в частности пакет Solid Works, который показал хорошие данные погрешности, применимые в гражданской авиации.
Литература:
- Statistical Data for the Boeing-747–400 Aircraft in Commercial Operations. U. S. Department of Transportation Federal Aviation Administration, 2005. 244 c.
- Мышенков В. И., Малашин А. А., Галахов Г. Д., Орехов А. Д., Пименов А. С., Пронин К. Н. Исследование пригодности ППП «NUMECA» для численного решения задач внешнего обтекания. Лесной вестник / Forestry Bulletin, 2018. Т. 22. № 6. С. 123–131.
- Пронин К. Н. Популяризация прикладной математики (на примере аэродинамики) для школьников и студентов. Техническое творчество молодёжи № 1 (137) 2023. 32–36 с.

