Problems of strength and deformability of monolithic reinforced-concrete girdless slabs with holes

In the modern literature questions of calculation of slabs with holes that complicates use of the results reached in the theory for the present are insufficiently taken up and frequently leads to application of the approached receptions.

In article the analysis of some modern methods is made: calculation of slabs by methods of the boundary collocation, realised for concrete parametres of a plate, and allowing to receive the reliable approached decision in the form of the formula in problems of a bend, number and the formula in problems of stability; calculation of a slabs with holes on a method of limiting balance in the kinematic way; the method of additional final elements combining three methods of calculation of designs - final elements, additional loadings and limiting conditions.

The primary goal was definition of the most simple and effective method, capable to form a basis not only for analytical calculations, but also for algorithms and the programs realising calculation of designs on limiting conditions, including for monolithic reinforced-concrete girdless slabs with holes.

Keywords: slabs with holes; a calculation method; a limiting condition; a boundary collocation; testing calculation; additional final elements.

Accidents in building happen presently for the various reasons. The basic harbinger - predictability and other physical properties of artificial accidents have been in detail considered and tabulated in Skorobogatov S.M., Homjakov V. A, Mordanov O.N. and Mordanova E.S.'s work «Classification of accidents of reinforced-concrete designs» [1]. One of possible ways of their prevention – correct calculation of buildings and constructions.

Slabs with holes are applied at erection of many designs, such, as elevators, the bunker, refrigerators, many-storeyed industrial buildings with the vertical production technology, the inhabited and public buildings sated with various communications.

Unfortunately, in our literature for the present questions of calculation of slabs with holes that complicates use of the results reached in the theory insufficiently are taken up and frequently leads to application of the approached receptions.

As example calculation of slabs by methods of a boundary collocation [2], result of researches of O.V.Mashkin and prof. V.V.Rogalevich – a method realised for concrete parametres of a plate, allows to receive the reliable approached decision in the form of the formula in problems of a bend, number and the formula in problems of stability. It is based on simple approximation of functions of a deflection, definition of one constant of the decision from a condition of orthogonality are nonviscous with approximating function, search of correcting parametres from a condition of a minimum root-mean-square the integrated is nonviscous in problems of a bend or a minimum of compressing effort in problems of stability.

For avoidance of a duality in calculation of designs when definition of efforts is made by methods of the theory of elasticity, and selection of sections of elements is carried out on a limiting condition, it is necessary to define possibility of a combination of two scientific directions: elastic work of slabs round holes and virtual work of slabs with linear plastic hinges. One more important question is possibility of correlation of sizes between these two conditions for definition of deflections of real designs.

Calculation of slabs on a method of limiting balance helps to solve this problem with an aperture. In R.V.Zinoveva, N.F.Zinovev, A. M.Frakter's work [3] results of experimentally-theoretical researches of the reinforced-concrete flat plates weakened by holes are stated, schemes of a break depending on the location of holes are analyzed and methods of calculation of square, rectangular and round slabs with holes of the various form are stated under different conditions of support. The examples resulted in the book, proves to be true that calculation of slabs with holes on a method of limiting balance comes easy and besides gives essential economy reinforcing to a steel. So, for the calculated plates this economy has made about 24 %.

The kinematic way of a method of the limiting balance which essence is in detail stated in S.M.Skorobogatov's uchebno-methodical grant [4] is applied to calculation of a slabs with holes.

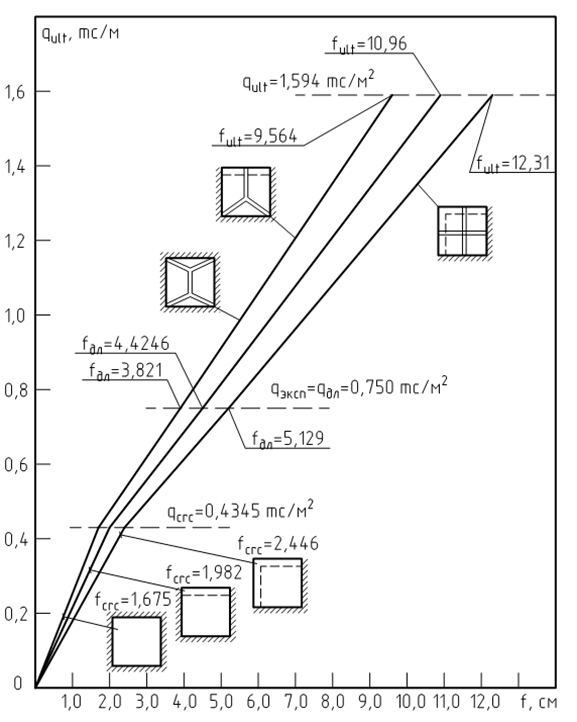
In view of complexity of a problem for design procedure construction results of the old experiences spent in Scientific-Research Institute of Concrete and Reinforced Concrete by A.A.Gvozdev, M.S.Krylov, etc. [5,6] have been used. Experiences have shown that the curve of deflections for convenience can be approximated two almost rectilinear sites at which speeds of increase of deformations essentially differ (see fig. 1). The first site (0 – q_crc) extends from the beginning loading till the moment of formation of the first cracks. The second site (q_crc – q_ult) extends from the moment of formation of cracks before occurrence of plastic hinges, i.e. to a settlement limiting condition (a predestruction stage).

Approximately the deflection of slabs at operational loading q_экс = q_дл can be defined on linear interpolation between a deflection f_crc, directly previous formation of the first cracks, and a deflection f_ult, directly previous exhaustion of bearing ability of plates:

(1)

where

Thus necessity for labour-consuming calculation of known and problem factor ψ_s completely disappears.

In the formula (1) q_экс = q_n – the operating operational standard in regular intervals distributed loading at factor of reliability γ_f = 1,0. In most cases q_экс = q_дл – it is long operating loading.

For the simple support slabs the deflection f_crc is defined as for an elastic plate under formulas of building mechanics. For the slabs jammed on a contour definition f_crc meets didactic and psychological difficulties. For a deflection f_crc it is necessary to accept sizes of a deflection of slabs at formation of cracks in flight (M_crc = R_bt._nW_pl) when cracks in jammings already are available. Therefore formulas of building mechanics for definition M_sp are not recommended [7].

Figure 1. Schemes of linear interpolation on a line between q_crc and q_ult.

The matter is that basic moments M_sup always more than M_sp [7]. The increase in flying moment M_sp to size M_crc leads to an increment of loading in flight. It causes increase in size of basic moment M_sup = M_crc + ΔM and as a whole increase in loading q + Δq.

The settlement scheme of a slab in this case can be presented in a kind the simple support the plate loaded by given loading Δq and unknown moments M_sup + ΔM along the long jammed party (i.e. from q + Δq).

For definition of sizes fcrc it is necessary to accept M_sup = M_crc and to use formulas for elastic plates. From loading M_sup = M_crc + Δ M (or q + Δq) for the scheme with a jamming on a contour:

(2)

where q and Δq are defined from the formula:

(3)

For elastic bodies usually use concept of cylindrical rigidity:

at (4)

For reinforced-concrete as elastic-plastic element or element with cracks in factor of Puassona do not use.

Moreover in modern norms and grants it is recommended to use special formulas for definition of size of rigidity D:

for element without cracks, (5)

for element with cracks. (6)

In formulas (5) and (6) use the resulted sizes, especially at long action of loading.

The greatest difficulty is caused by definition f_ult which depends on curvature [7]:

(7)

Deflection definition f_ult meets methodical difficulties. In connection with uncertainty of sizes of the basic moments of process loading, after cracking, there is a little defined a size σ_s (or R_{s, n}). It is necessary to rebuke the following softening a sharpness of a problem. At small percent of reinforcing that is characteristic for slabs designs, in the formula (7) between size (1/r) and R_s,_n there is almost rectilinear dependence. Therefore it is not so important, what size instead of R_{s, n} it is possible to use.

However, despite all advantages of application of a method of calculation on limiting conditions, it represents a serious problem at a combination to the method of final elements focused on use of today's program complexes.

Modern computer programs of calculation of building designs poorly coordinate the general methods of the decision of problems of building mechanics to the modern norms considering new physicomechanical models. In many programs linear dependences for concrete are used. As a result of norm of designing and computer methods develop different ways. In some programs plastic deformations are considered by means of uniform, ill-founded, and too approximated factors. Concealing about the applied algorithms reduces trust to program complexes. Vulnerability girdless overlappings in deflections because of small rigidity doesn't exclude necessity of testing calculations (after calculations on the computer) on the first and second groups of limiting conditions.

For elimination of this contradiction it is necessary to solve a problem of reception of a limiting condition of a counted design means of a method of final elements. The same is possible only under condition of the account of all nonlinear properties shown by this design by the time of achievement by it of a limiting condition, i.e. at the account of degree of influence and time of occurrence of each separate nonlinear property.

The given problem is represented very actual in modern conditions. One of possible ways of its decision is the method of additional final elements stated in the monography of A. V.Ermakova [8], and combining three methods of calculation of designs: final elements, additional loadings and limiting conditions.

According to a technique of this calculation process of change of nonlinear properties of a separate final element at gradual achievement of a limiting condition is modelled by it by means of specially developed additional final elements, allowing to change properties of a basic element. Offered additional final elements allow to build a vector of additional loadings irrespective of character of observable nonlinear properties of basic elements.

Additional loadings can be constructed in three ways on a basis: the additional final elements of a general view changing matrixes of rigidity of basic elements; the additional elements of the first type changing a tension of basic elements, and the additional elements of the second type changing the deformed condition of the basic final elements.

For the description of a limiting condition of all design it is offered to use the ideal model of its destruction representing the settlement scheme of this design at the moment of limiting balance. It consists of two: the settlement scheme from the basic final elements with linear properties and the settlement scheme from additional elements with the nonlinear properties, corresponding to the given stage of a limiting condition.

The settlement scheme from additional elements changes the initial scheme from linear elements so that it corresponded to the stage of a limiting condition of a design reached to the given moment; in a limiting stage it transforms the initial settlement scheme into ideal model of destruction of a design.

From the aforesaid it is possible to draw a conclusion that the offered technique is sufficient is simple and can form a basis for algorithms and the programs realizing calculation of designs on limiting conditions, including for calculation monolithic reinforced-concrete girdless slabs with holes.

References:

1. S. Skorobogatov, V. Khomyakov, O. Mordanov, E. Mordanova. Classification of catastrophes of reinforced concrete structures // Herald of Ural State University of Railway Transport, 2010, №4. – p. 63–71. ISSN 2079-0392 (In Russia: Скоробогатов С.М., Хомяков В.А., Морданов О.Н., Морданова Е.С. Классификация катастроф железобетонных конструкций // Вестник УрГУПС, 2010, №4. – С. 63-71.) ISSN 2079-0392.

2. Mashkin O.V, Rogalevich V.V., 2011. Calculation of plates by methods of a boundary collocation: the monography. Ekaterinburg: Publishing house AMB, 2011. – pp. 76 (In Russia: Машкин О. В., Рогалевич В. В., 2011. Расчет пластин методами граничной коллокации: монография. Екатеринбург: Издательство АМБ, 2011. – 76 с.)

3. Zinoveva R.V, etc, 1975. Reinforced-concrete slabs with holes. – М: Stroyizdat, 1975. – рр. 112. (In Russia: Зиновьева Р.В. и др., 1975. Железобетонные плиты с отверстием. – М.: Стройиздат, 1975. – 112 с.)

4. S.M.Skorobogatov. Checking calculations of reinforced concrete monolithic flat plate floors of service limit state (deflections, cracks) / For bachelors, engineers and graduate students of specialty Industrial and Civil Engineering. – Yekaterinburg: Ural State University of Railway Transport, – 2011. – pp. 80 (In Russia: Скоробогатов С.М. Поверочные расчеты безбалочных бескапительных монолитных железобетонных перекрытий по второй группе предельных состояний (прогибы, трещины) / Для бакалавров, инженеров и магистрантов специальности ПГС.­­­­ – Екатеринбург: УрГУПС, – 2011. – 80 с.)

5. Guide for analysis of statically indeterminate reinforced concrete structures / Scientific-Research Institute of Concrete and Reinforced Concrete in the USSR State Construction Committee. – Moscow: Stroiizdat, 1975. – pp. 193 (In Russia: Руководство по расчету статически неопределимых железобетонных конструкций / НИИ бетона и железобетона Госстроя СССР. – М.: Стройиздат, 1975. – 193 с.)

6. Guide for designing reinforced concrete constructions with flat slab floors / Scientific-Research Institute of Concrete and Reinforced Concrete of the USSR State Construction Committee, Central scientific-research, design and experimental institute of industrial buildings and structures of the USSR State Construction Committee, the Ural design and scientific-research institute of the USSR State Construction Committee. – Moscow: Stroiizdat, 1979. – pp. 63 (In Russia: Руководство по проектированию железобетонных конструкций с безбалочными перекрытиями / НИИ бетона и железобетона Госстроя СССР, Центр. н.-и. и проект.-эксперим. ин.-т пром. зданий и сооружений Госстроя СССР, Урал. проект. и н.-и. ин-т Госстроя СССР. – М.: Стройиздат, 1979. – 63 с.)

7. Under the editorship of A.B.Golyshev, 1990. Designing of reinforced -concrete designs. Kiev, Budivelnik, 1990. (See head «Calculation of slabs», pp. 360-373). (In Russia: Проектирование железобетонных конструкций // Справочное пособие [Под ред. А.Б. Голышева]. – Киев, Будiвельник, 1990. – 543 с. (см. главу «Расчет плит», стр. 360-373)).

8. Ermakova A.V., 2007. Method of additional final elements for calculation of reinforced-concrete designs on limiting conditions. М: АСВ, 2007. (In Russia: Ермакова А.В., 2007. Метод дополнительных конечных элементов для расчета железобетонных конструкций по предельным состояниям. – М.: АСB, 2007. – 128 с.).