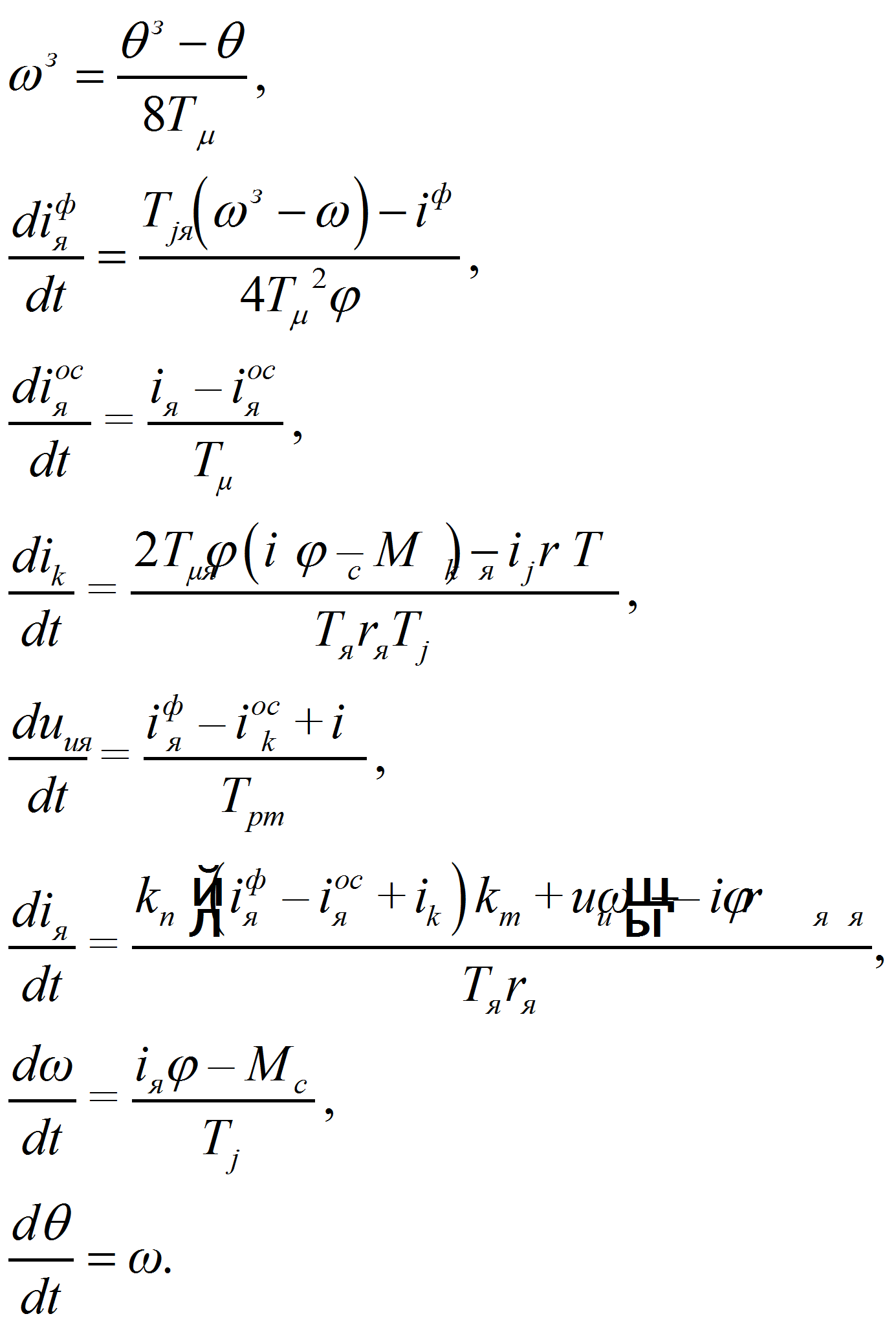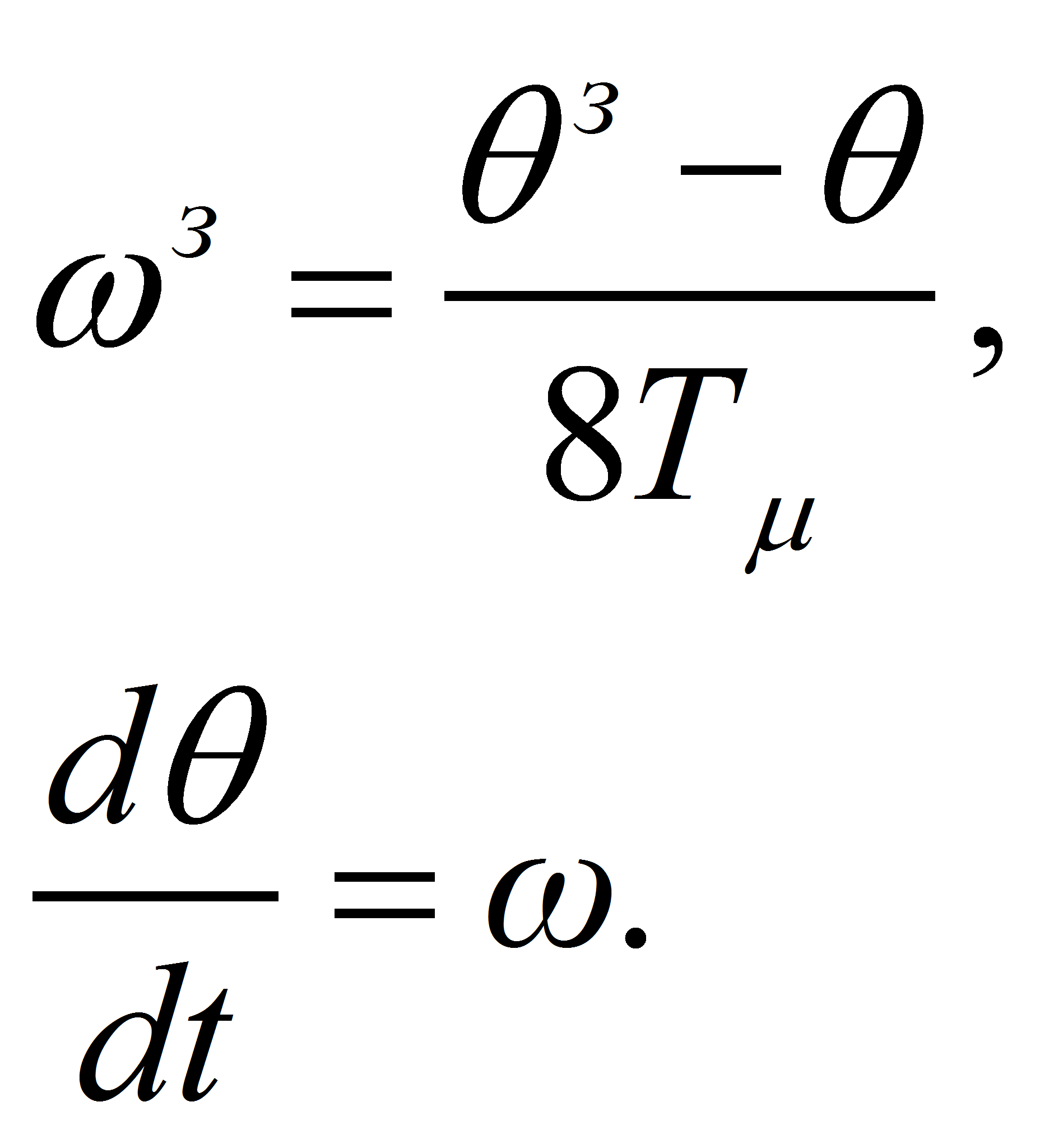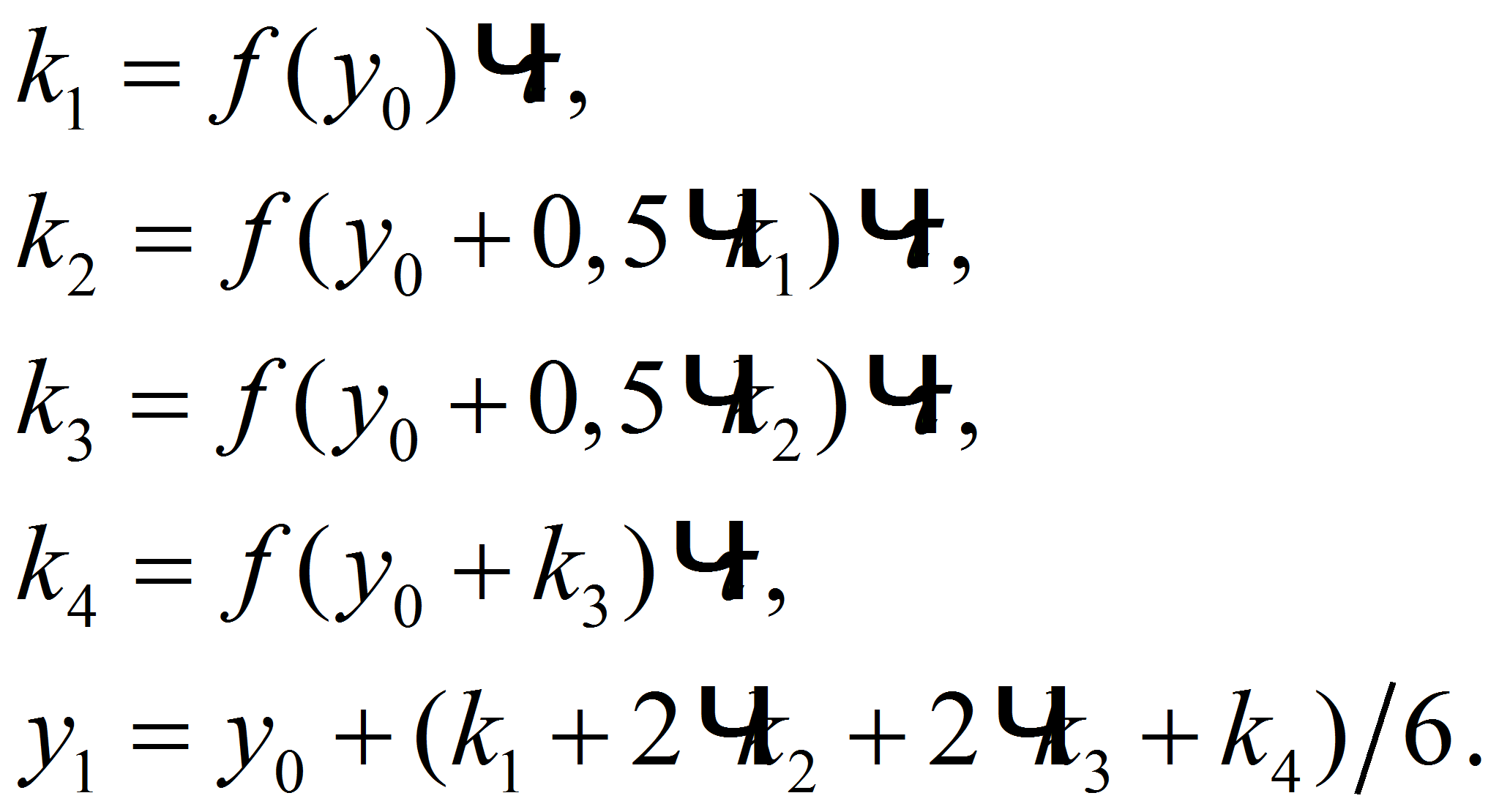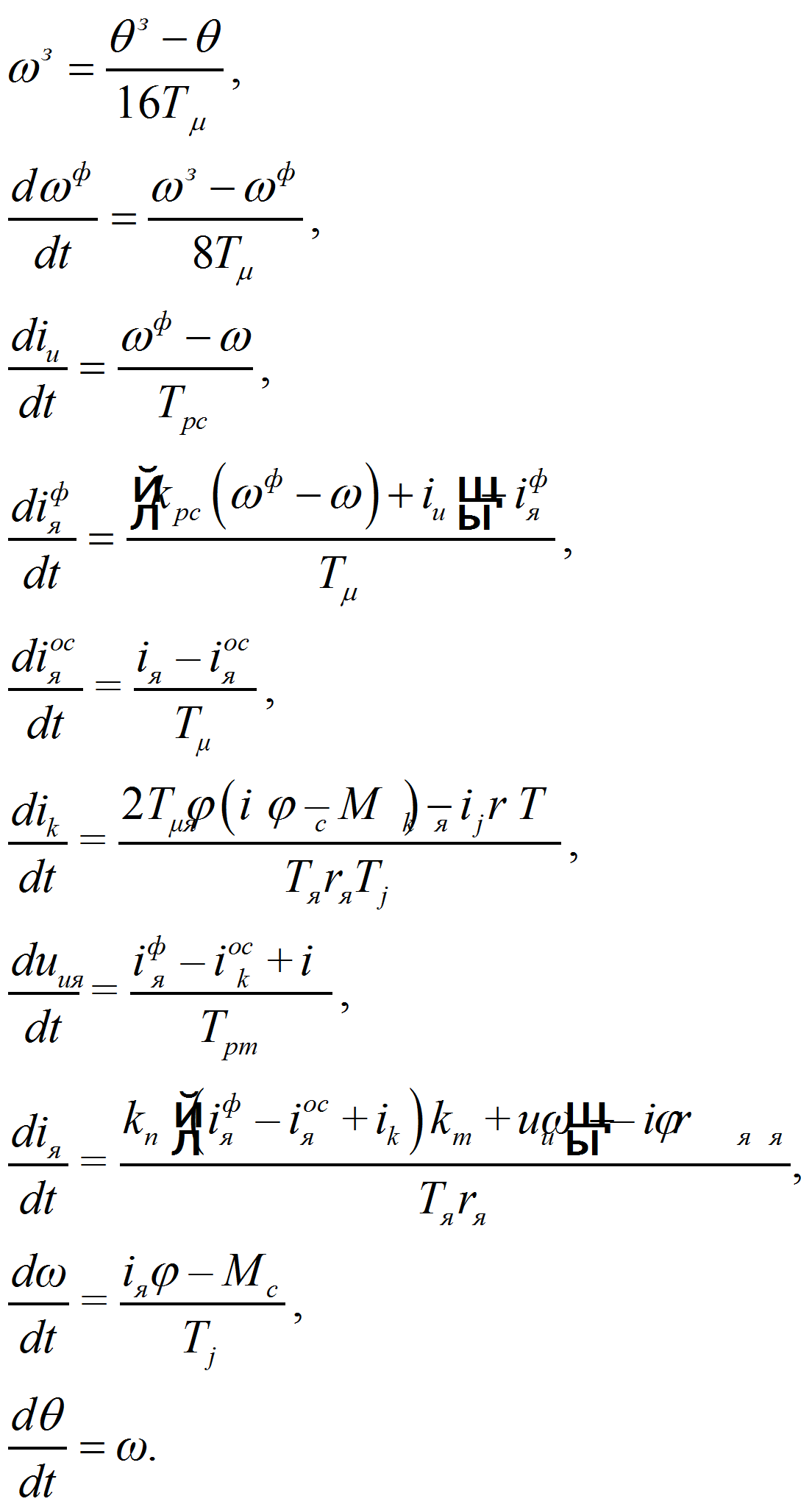Программирование контура положения в Delphi

В пакете учебных программ необходимо иметь примеры программирования в Delphi многоконтурных систем подчиненного регулирования электроприводов. Системы автоматического регулирования положения строятся путем дополнения рассмотренных в [2] САР скорости системой автоматического регулирования положения (или угла поворота вала двигателя). Таким образом, для регулирования положения используется трехконтурная структура, содержащая внутренний контур регулирования тока якоря, промежуточный контур регулирования скорости и внешний контур регулирования положения. Промежуточная САР скорости может быть как одно -, так и двукратной, что предопределяет и тип САР положения.

Вариант 1. Однократная система автоматического регулирования положения.

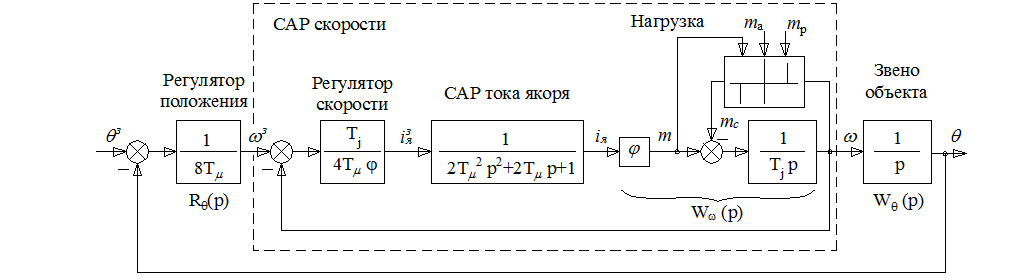
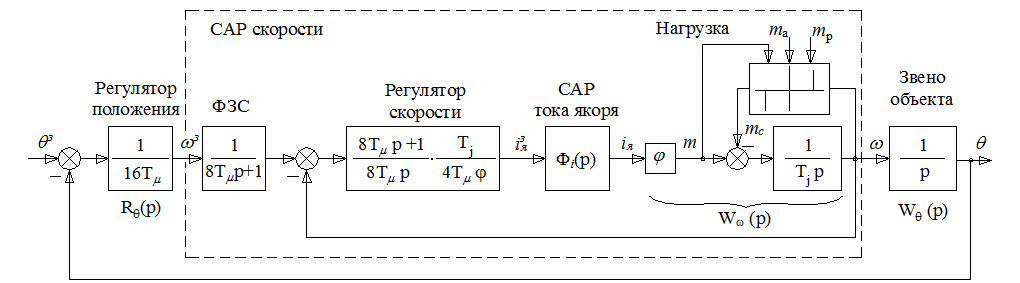
На рис.1. приведен контур положения, состоящий из сумматора, пропорционального регулятора скорости, внутреннего контура тока (САР тока якоря), механической части привода с моделируемой нагрузкой в Delphi и обратными связями по скорости и положению.

Рис.1. Структурная схема однократной САР положения

Для структурной схемы однократной САР положения (рис.1.) запишем следующую систему дифференциальных уравнений:

Данная система уравнений дополняет аналогичную систему дифференциальных уравнений, приведенных в [2], для однократной САР скорости двумя уравнениями:

Решение данной системы дифференциальных уравнений произведем на языке программирования высокого уровня Delphi методом Рунге-Кутты 4-го порядка. Для реализации поставленной задачи запишем вышеуказанные уравнения как функции в разделе private:

function diaf(iaf,ioc,ik,uu,ia,v,t:real):real;

function dioc(iaf,ioc,ik,uu,ia,v,t:real):real;

function dik(iaf,ioc,ik,uu,ia,v,t:real):real;

function duu(iaf,ioc,ik,uu,ia,v,t:real):real;

function dia(iaf,ioc,ik,uu,ia,v,t:real):real;

function dv(iaf,ioc,ik,uu,ia,v,t:real):real;

function Mc(v,t:real):real;

После нажатия на сочетание клавиш Ctrl+Shift+C получим заготовки, которые компилятор создаст сам. В эти заготовки запишем уравнения:

function TMainForm.dia(iaf,ioc,ik,uu,ia,v,t:real): real;

begin

dia:=(kp*((iaf-ioc+ik)*kt+uu)-v*phi-ra*ia)/(ra*Ta);

end;

function TMainForm.diaf(iaf,ioc,ik,uu,ia,v,t:real): real;

begin

diaf:=((Tj*(vzad-v)/(4*Tmu*phi))-iaf)/Tmu;

end;

function TMainForm.dioc(iaf,ioc,ik,uu,ia,v,t:real): real;

begin

dioc:=(ia-ioc)/Tmu;

end;

function TMainForm.duu(iaf,ioc,ik,uu,ia,v,t:real): real;

begin

duu:=(iaf-ioc+ik)/Tt;

end;

function TMainForm.dv(iaf,ioc,ik,uu,ia,v,t:real):real;

begin

dv:=(ia*phi-Mc(v,t))/Tj;

end;

function TMainForm.dik(iaf,ioc,ik,uu,ia,v,t:real): real;

begin

dik:=(2*Tmu*phi*(ia*phi-Mc(v,t))/(ra*Tj)-ik)/Ta;

end;

function TMainForm.Mc(v,t:real):real;

begin

if McDataForm.McCheckBox.Checked then

begin

Mp:=M0+A1*abs(v)+A2*sqr(v)+A3*abs(Power(v,3));

Mtp:=1.3*abs(M0);

if abs(v)>0.0001 then Mcp:=Mp*sign(v)

else

begin

if abs(M-Ma)>Mtp then Mcp:=Mtp*sign(M-Ma)

else Mcp:=M-Ma

end;

Mc:=Mcp+Ma;

end;

end;

Для определения математических функций необходимо прописать модуль «Math» в разделе uses. Создадим раздел констант между разделами type и var с постоянными:

const

Tj=0.423; // Данные двигателя Д31: 6,8 кВт, 220 В, 37 А,

Ta=0.034; // 880 об/мин.

ra=0.107;

phi=1;

kp=1.393;

Tmu=0.01;

kt=ra*Ta/(2*kp*Tmu);

Tt=2*kp*Tmu/ra;

В разделе var опишем глобальные переменные:

var

MainForm: TMainForm; – В данном примере имя формы - MainForm

iaz,kt,Tt,M,ep,ea,ik,vzad,tetazad,teta,

{Mc} Mc,Mp,Mtp,Mcp:Real;

Поместим на форму 2 компонента TChart из вкладки Additional и компонент Button из вкладки Standart.

Щелкнув два раза на каждом компоненте TChart левой кнопкой мыши, появится окно, в котором на вкладке Series нажимаем на кнопку Add. Далее выбираем тип графика FastLine, убираем галочку 3D и нажимаем ОК. На вкладке Legend убираем галочку напротив Visible и нажимаем Close.

Перейдем на вкладку Events в окне Object Inspector, предварительно выделив кнопку.

Щелкнув два раза по позиции OnClick будет автоматически создана процедура по нажатии данной кнопки:

procedure TMainForm.Button1Click(Sender: TObject);

begin

end;

Опишем переменные необходимые только для данной процедуры. Данный раздел необходимо описать между строками «procedure TMainForm.Button1Click (Sender: Tobject);» и «begin»:

var

k1ik,k2ik,k3ik,k4ik,

k1ioc,k2ioc,k3ioc,k4ioc,

k1iaf,k2iaf,k3iaf,k4iaf,

k1uu,k2uu,k3uu,k4uu,

k1uy,k2uy,k3uy,k4uy,

k1ia,k2ia,k3ia,k4ia,

k1v,k2v,k3v,k4v,

dv0,dia0,t0,duu0,dioc0,diaf0,dik0,

dv1,dia1,duu1,dioc1,diaf1,dik1,

t,dt,k:Real;

i:Integer;

Зададим начальные условия:

diaf0:=0;

dioc0:=0;

dik0:=0;

duu0:=0;

dia0:=0;

dv0:=0;

t0:=0;

tetazad:=0.1;

i:=0;

Назначим шаг интегрирования:

dt:=0.0005;

Далее зададим цикл:

i:=0;

while i<1000 do

begin

end;

В данном цикле опишем процедуру расчета системы дифференциальных уравнений методом Рунге-Кутты 4-го порядка. Данный метод описывается следующим образом:

Тогда:

while i<1000 do

begin

{M} M:=dia0*phi;

Mc(dv0,t0);

// Задание на скорость

vzad:=(tetazad-teta)/(8*Tmu);

// diaf

k1iaf:=diaf(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2iaf:=diaf(diaf0+0.5*k1iaf,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k3iaf:=diaf(diaf0+0.5*k2iaf,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k4iaf:=diaf(diaf0+k3iaf,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

diaf1:=diaf0+(k1iaf+2*k2iaf+2*k3iaf+k4iaf)/6;

// dioc

k1ioc:=dioc(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2ioc:=dioc(diaf0,dioc0+0.5*k1ioc,dik0,duu0,dia0,dv0,t0)*dt;

k3ioc:=dioc(diaf0,dioc0+0.5*k2ioc,dik0,duu0,dia0,dv0,t0)*dt;

k4ioc:=dioc(diaf0,dioc0+k3ioc,dik0,duu0,dia0,dv0,t0)*dt;

dioc1:=dioc0+(k1ioc+2*k2ioc+2*k3ioc+k4ioc)/6;

// dik

k1ik:=dik(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2ik:=dik(diaf0,dioc0,dik0+0.5*k1ik,duu0,dia0,dv0,t0)*dt;

k3ik:=dik(diaf0,dioc0,dik0+0.5*k2ik,duu0,dia0,dv0,t0)*dt;

k4ik:=dik(diaf0,dioc0,dik0+k3ik,duu0,dia0,dv0,t0)*dt;

dik1:=dik0+(k1ik+2*k2ik+2*k3ik+k4ik)/6;

// duu

k1uu:=duu(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2uu:=duu(diaf0,dioc0,dik0,duu0+0.5*k1uu,dia0,dv0,t0)*dt;

k3uu:=duu(diaf0,dioc0,dik0,duu0+0.5*k2uu,dia0,dv0,t0)*dt;

k4uu:=duu(diaf0,dioc0,dik0,duu0+k3uu,dia0,dv0,t0)*dt;

duu1:=duu0+(k1uu+2*k2uu+2*k3uu+k4uu)/6;

// dia

k1ia:=dia(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2ia:=dia(diaf0,dioc0,dik0,duu0,dia0+0.5*k1ia,dv0,t0)*dt;

k3ia:=dia(diaf0,dioc0,dik0,duu0,dia0+0.5*k2ia,dv0,t0)*dt;

k4ia:=dia(diaf0,dioc0,dik0,duu0,dia0+k3ia,dv0,t0)*dt;

dia1:=dia0+(k1ia+2*k2ia+2*k3ia+k4ia)/6;

// dv

k1v:=dv(diaf0,dioc0,dik0,duu0,dia0,dv0,t0)*dt;

k2v:=dv(diaf0,dioc0,dik0,duu0,dia0,dv0+0.5*k1v,t0)*dt;

k3v:=dv(diaf0,dioc0,dik0,duu0,dia0,dv0+0.5*k2v,t0)*dt;

k4v:=dv(diaf0,dioc0,dik0,duu0,dia0,dv0+k3v,t0)*dt;

dv1:=dv0+(k1v+2*k2v+2*k3v+k4v)/6;

// teta

teta:=teta+dv0*dt; // Расчет угла поворота

Series1.AddXY(t0,teta); // Выводим график угла поворота

Series2.AddXY(t0,dv0); // Выводим график скорости

Inc(i);

t0:=t0+dt;

diaf0:=diaf1;

dioc0:=dioc1;

dik0:=dik1;

duu0:=duu1;

dia0:=dia1;

dv0:=dv1;

end;

После нажатия на кнопку Run (F9) появится окно программы, нажимаем на кнопку и получаем следующие результаты:

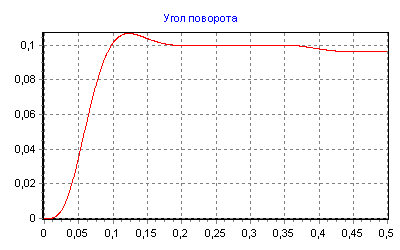
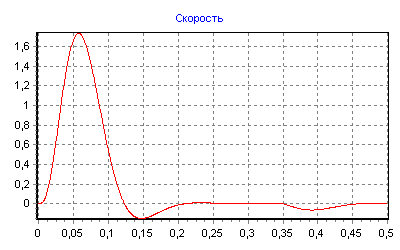
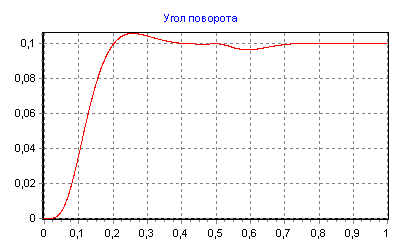
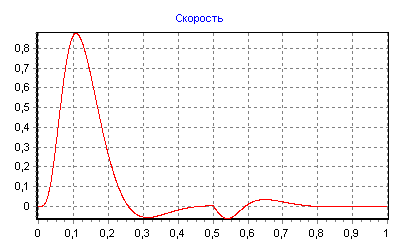
На рис.2 представлен результат моделирования контура положения на основе однократной САР скорости.

Рис.2. Реакция однократной САР положения

на скачок задающего воздействия и наброс нагрузки

На рис.2 также изображена реакция САР на скачок активного момента статического сопротивления на валу двигателя в момент времени равный 0,35. Данное перемещение представляет собой статическую ошибку по положению, вызванную приложением активной статической нагрузки к валу двигателя.

Параметры графика θ(t) соответствуют стандартам третьего контура системы подчиненного регулирования, для которого время достижения максимума равно 18 T_μ при перерегулировании 6,2%.

Вариант 2. Двукратная система автоматического регулирования положения.

Дополнение рассмотренной выше позиционной САР еще одним контуром регулирования положения (аналогично тому, как на базе однократных САР строятся двукратные САР скорости). В этом случае образуется двукратная САР положения, представляющая собой четырехконтурную систему подчиненного регулирования.

Рис.3. Структурная схема двукратной САР скорости

По структурной схеме, изображенной на рис.3 можно записать следующую систему дифференциальных уравнений, используя методику из [2]:

Решение данной системы дифференциальных уравнений ничем не отличается от приведенного выше, за исключением передаточной функции регулятора положения. Для двукратной САР положения он примет вид:

После нажатия на кнопку Run (F9) появится окно программы, нажимаем на кнопку и получаем следующие результаты:

Рис. 4. Реакция однократной САР положения

на скачок задающего воздействия и наброс нагрузки

На рис.4 также изображена реакция САР на скачок активного момента статического сопротивления на валу двигателя в момент времени равный 0,5. Скачкообразное увеличение активной нагрузки на валу вызывает временное (динамическое) изменение положения, т.е. динамическую ошибку, которая затем полностью исключается совместным действием регуляторов положения и скорости.

Полученные результаты соответствуют общепринятым теоритическим положениям, приведенным в [1].

Литература:

1. Шрейнер Р.Т. Системы подчиненного регулирования электроприводов. - Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 279 с.

2. Емельянов А.А., Медведев А.В., Кобзев А.В. Программирование контура скорости в Delphi // Молодой Ученый – 2012. – №4. – С.1–8.

3. Архангельский А.Я. Программирование в Delphi для Windows. Версии 2006, 2007, Turbo Delphi. – М.: ООО «Бином-Пресс», 2007.– 1248 с.