One of the most significant scientific discoveries of recent decades is the discovery of deterministic chaos in dynamical systems. The essence of this discovery is that a fully defined dynamic system, in the absence of any random influences, begins to behave in a chaotic manner. But with this randomness, upon closer examination, it is possible to find several patterns in its behavior, which distinguishes this phenomenon from classical random processes. Unlike classical random processes, the phenomenon of deterministic chaos can be repeated many times in field and laboratory experiments.
Keywords: stability, robustness, catastrophe, stationary state, Hurwitz criterion, aircraft.
Одним из наиболее значительных научных открытий последних десятилетий является открытие детерминированного хаоса в динамических системах. Суть этого открытия заключается в том, что полностью определенная динамическая система при отсутствии каких-либо случайных воздействий начинает вести себя хаотично. Но при такой случайности при ближайшем рассмотрении можно обнаружить несколько закономерностей в ее поведении, что отличает это явление от классических случайных процессов. В отличие от классических случайных процессов, явление детерминированного хаоса может многократно повторяться в полевых и лабораторных экспериментах.
Ключевые слова: устойчивость, робастность, катастрофа, стационарное состояние, критерий Гурвица, воздушное судно.
On the eve of the Head of State Kassym-Jomart Tokayev delivered another Message to the people of Kazakhstan «Unity of the people and systemic reforms are a solid foundation for the prosperity of the country» with a number of initiatives regarding the socio-economic development of the country. Addressing Kazakhstanis, the President called the 30th anniversary of Independence the highest value of our state. In his annual Address, the Head of State noted the importance of digitalization in Kazakhstan, as well as, «Kazakhstan should become the central digital hub in Eurasia». JSC NC «Kazakhstan Garysh Sapary» supports the initiatives given by the Head of State and intends to further develop space technologies, expanding the range of tasks and capabilities of space monitoring and remote sensing of the Earth. As part of the Address, the company's specialists will continue to introduce innovative technologies into the national economy of the state and increase productivity efficiency. The use of digital technologies in our country implies the use of the concept of integrated organization of the design, development and testing of onboard spacecraft control systems and their software. The main idea of the concept is the use of simulation stands at all stages of the life cycle of creating a Spacecraft. The success of the rocket and space industry is largely determined by the contribution to its development. In the space field of the USA, there has always been an understandable tendency to reduce the mass of satellites and improve in the field of their automation. However, today they have switched not just to small, micro and nano-sized devices, but special systems are being created, numbering thousands of automated satellites. Many countries and organizations, including private companies, are involved in their development. What used to be the exclusive prerogative of America is becoming very widespread all over the world. This allows us to talk about a qualitative change in the trends in the development of rocket and space technology and their automation. I think that our country is capable of developing the rocket and space industry to such a scale. In this regard, it became necessary to build such automatic systems that, with changing parameters of the object and the influence of external disturbances, would not only remain in a stable state, but also provide the required quality of functioning.
This, in my opinion, is how the engineering of our time should work:
Search for the most effective solutions, without reference to existing solutions. It is clear that linear combinations have all been considered for a long time, and the study and modeling of nonlinear relationships is considered difficult. The parametric approach just allows you to see everything that is not usually looked at. Allows, but requires capacity.
Chaos, no matter how interesting it is, is only part of the complex behavior of nonlinear systems. There is also a phenomenon that defies intuitive awareness, which could be called anti-chaos. It is expressed in the fact that some very disordered systems spontaneously «crystallize», acquiring a high degree of order.
The phenomena of deterministic chaos are possible only in nonlinear systems. Therefore, with the discovery of deterministic chaos, previously existing illusions about arbitrarily adequate descriptions of real processes using linear mathematical models were completely dispelled. The view of nonlinear systems as some «cosmetic» improvement of linear models is outdated.
The combination of controllability and plasticity, according to many researchers, is the reason that chaotic dynamics is a characteristic type of behavior for many vital subsystems of living organisms. For example, the chaotic nature of the heart rhythm allows the heart to flexibly respond to changes in physical and emotional stress, providing a margin of dynamic strength.
In the works of Beisenby M. A. [5], Utepebergenova A. T. [6], Satybaldina D. K. [7] and Ten V. V. [8], a study of the dynamic properties of control systems in the class of one-parameter (catastrophe «fold»), two-parameter (catastrophe «assembly») and three-parameter (disasters «dovetail» and «elliptical ombilika») structurally stable mappings, respectively, was carried out. The obvious difference is that in the first case there is one control parameter, in the second — two, and in the third and fourth three control parameters, respectively, while in the first three cases there is one phase coordinate, and in the fourth — two phase coordinates. The three-parameter structurally stable mapping considered in this paper (the «hyperbolic ombilica» catastrophe) has three control parameters (controller parameters) and two phase coordinates, which gives more opportunities for designing control systems, generally consisting in the following:
1) The possibility of varying coordinates (indexes);
2) Expansion of the stability area due to the appearance of a new control parameter.
It is obvious that similar mechanisms of reliable and flexible response to disturbances and control actions are characteristic of other complex systems that successfully operate in a volatile environment. Such systems should be sensitive enough to «innovative» disturbances and react by correcting «trajectories» in order to have the ability to evolve, but at the same time remain on their attractor and maintain the type of behavior characteristic of this system as a whole. If the system loses these properties, then even a significant margin of «mechanical strength» may be insufficient in relation to the effects of specific small dynamic disturbances, and an outwardly prosperous system may lose stability and collapse.
The control of space aircraft (JIA) is carried out based on information from various measuring systems. Usually measuring systems are combined into measuring complexes, and, as a rule, consist of inertial navigation systems (INS), GPS satellite radio navigation systems.
With the regular movement of KJIA, the exact characteristics of modern measuring systems fully meet the requirements for the accuracy of navigation definitions. However, with intensive maneuvering, increased requirements are placed on accuracy and measurement information. The development and production of more accurate measuring systems requires a lot of time and financial costs. Therefore, to increase the accuracy of navigation information to save money, it is proposed to carry out algorithmic signal processing of existing measuring systems.
The scientific novelty of the research and the results obtained lies in the analysis of the most promising control systems and the structures of control systems developed on its basis in the mode of deterministic chaos. In the structures of the control systems of the SPACECRAFT, it is proposed to use blocks of prediction and comparison of the result of an action to predict information about the trajectory of movement and errors in determining navigation information, as well as correction of this information.
From the results obtained, it follows that with fixed positive values, the system is stable for any values, both positive and negative parameters. A system unstable in one stationary state becomes stable in another, and vice versa, which is confirmed by the results of a numerical experiment conducted using the Vissim 6.0 software package (Figures 1–4).
Figures 1–2 show the results of a numerical experiment conducted using Vissim 6.0 according to the scheme from Figure 1, when the parameters are (fixed), we change.
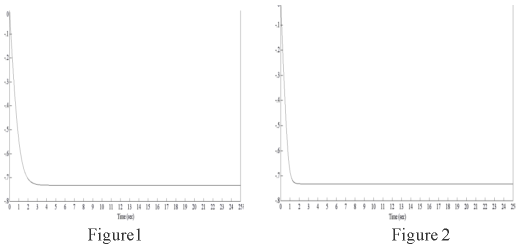
Figures 3–4 show the results of a numerical experiment conducted with the values of the variables already known to us.
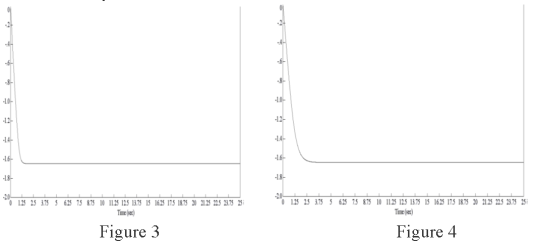
Therefore, we are convinced that the linearized model of the aircraft motion control system due to the introduction of the control law in the form of a catastrophe into the control circuit «hyperbolic ombilica» becomes robustly stable within indefinitely large limits of changing the parameters of the control object and the set parameters of the controller and. The presented results of the numerical experiment obtained using the Vissim 6.0 simulator program confirm the results obtained. It follows that with some rather small deviation from the reference values, based on the results of the analysis of the linearized model, it is possible to assume about the robust stability of the aircraft control system.
References:
- Besekersky V. A., Nebylov A. V. Robust automatic control systems. — M.: Nauka, Moscow, 1983. — 239 p. 11
- Polyak B. T., Shcherbakov P. S. Robust stability and control — M.: Nauka, Moscow, 2002. — 303 p.
- Methods of robust, neuro-fuzzy and adaptive control: Textbook / Ed.D. Egupova; the 2nd edition, stereotyped. — M.: Izd-vo MGTU imeni N. Uh. Bauman, Moscow, 2002. — 744 p., Il.
- Thompson, George. M. T. Instabilities and catastrophes in science and engineering: Per. from English. — M.: Mir, 1985. — 254 p., Il.
- Beisenbi M. A. Models, methods of analysis and synthesis of extremely stable control systems, Doctor of Technical Sciences, Almaty, 1998. — 205 p.
- Utepbergenova A. I. Methods of analysis and synthesis of control systems in the class of structurally stable mappings (on the example of an assembly disaster), Candidate of Technical Sciences, Almaty, 2002. — 134 p.
- Satybaldina D. K. Study of robustness of control systems built in the class of disasters dovetail, Candidate of Technical Sciences, Almaty, 2007. — 140 p.
- Nicklas J. C. and H. C. Vivian, Derived-rate Increment Stabilization: Its Appli-cation to the Attitude-control Problem, presented at the Joint Automatic Con-trol Conference, Boulder, Colo. June 28–30, 1961.
- Chegeni E., Zandieh M., Ebrahimi J. Attitude Control of Satellite With Pulse-Width PulseFrequency (PWPF) Modulator Using Generalized Incremental Predictive Control // Majlesi Journal of Electrical Engineering Vol. 8, No. 3, September 2014, p. 25–31







