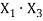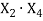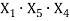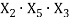В данной статье рассмотрена мостиковая структура событий, поскольку она является структурно-сложной и не сводится ни к последовательной, ни к параллельной. Это обусловлено промежуточным событием, которое выполняет функцию так называемого мостика. Работоспособность или защита в таких структурах зависит от одновременного состояния некоторой цепочки событий.
Ключевые слова: мостиковая схема, объект, безопасность, атака, вероятность.
In this article, the bridging structure of events is considered, since it is structurally complex and is not reduced to either sequential or parallel. This is due to an intermediate event that performs the function of the so-called bridge. The performance or protection in such structures depends on the simultaneous state of a certain chain of events.
Keywords: bridge scheme, object, security, attack, probability.
В настоящее время информация является одним из наиболее ценных ресурсов. Это влечёт за собой появление всё большего количества угроз безопасности. Объект защиты может быть представлен различными структурными схемами, как структурно-простыми (последовательная и параллельная), так и структурно-сложными.
Простейшей структурно-сложной схемой является мостовая, которая не может быть сведена к параллельной или последовательной структуре. Она так же применятся в теории надёжности технических систем. Для ее построения потребуется минимум пять элементов. Она представляет из себя четыре вершины, соединенные пятью ребрами [1, 2].
Каждая структура модели имеет следующие элементы:
Узлы — точки, на которых представлено текущее состояние системы, т.е. можно увидеть была ли реализована угроза или нет.
Ребра — сами угрозы. Угроза является функцией, принимающей значения от 0 до 1. Ввиду более сложной структуры мостовая схема имеет элемент X 5 , который влияет на выполнение мостиковой угрозы.
На структурной схеме особенность мостиковой структуры выглядит как общий элемент. При этом он создаёт взаимосвязь возможных сценариев, откуда и появляется мостиковая схема. Структурно-сложные системы распределены не только среди информационных систем, но и в среде организационных, банковских и гуманитарных систем.
В данной статье описывается простейший вариант мостиковой структуры без дополнительных составных угроз, потому что от составных схем всё равно можно прийти к простейшей. Например:
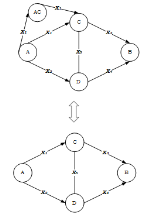
Рис. 1. Сведение мостиковой структуры
На практике мостовая структура может быть представлена как схема проникновения из одного помещения в другое (рисунок 2). Ниже приведён пример, где A — начальное событие, B — конечное.
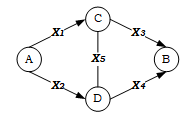
Рис. 2. Представление путей атаки в виде графа
Чтобы выразить сложное событие как результат логических операций над его составляющими воспользуемся структурной функцией.
Построим СФ для мостиковой структуры, представленной на рисунке 2. Приведём в таблице 1 все пути, по которым может происходить атака от угрозы А к уязвимости В.
Таблица 1
Кратчайшие пути атаки в мостиковой структуре событий
|
Номер пути |
Путь |
Формула события |
|
1 |
ACB |
|
|
2 |
ADB |
|
|
3 |
ACDB |
|
|
4 |
ADCB |
|
Появление одного события не исключает появление другого, тогда «дороги» перемножаются.
Тогда СФ представляет сумму путей:
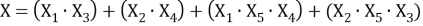
Можно представить CФС как:
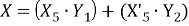
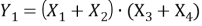
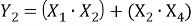
Граф, полученной СФ для графа на рисунке 2, представлен на рисунке 3.
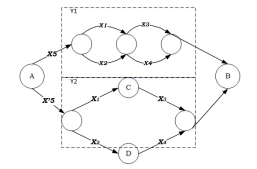
Рис. 3. Преобразование СФ с мостиковой структурой
Для работы со структурно-сложными структурами воспользуемся индикаторной функцией (далее ИФ). ИФ позволяет выразить сложное событие как результат арифметических действий. Индикатор указывает на то, произошло событие (0) или не произошло (1). Получим ИФ для выражения (4):
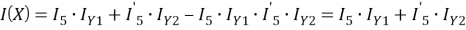
События Y 1 и Y 2 имеют простую структуру, что позволяет получить ИФ:
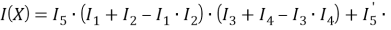
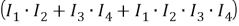
В результате рассмотрения мостиковой структуры можно сделать следующие выводы:
— составные мостиковые структуры могут быть сведены к более простым;
— при разных вероятностях реализации угроз наибольшее внимание стоит обращать на промежуточный элемент (мостик);
— СФ используется для выражения события в виде логических операций над его составляющими;
Литература:
1. И. А. Рябинин Cтруктурно-сложные системы и их формализация с помощью функций алгебры логики. — 2011.
2. Надежность технических систем. Методические указания и контрольные задания по курсу «Основы теории надежности». Сост. е.В.Сугак.- Красноярск: Сиб.аэрокосм.академия, 2001.- 42 с