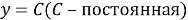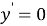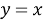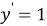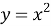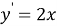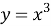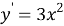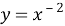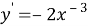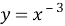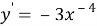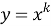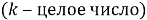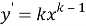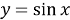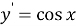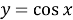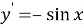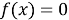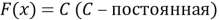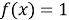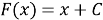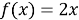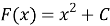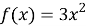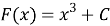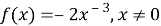В статье автор рассматривает урок открытия нового знания на примере темы «Первообразная». Здесь раскрываются методические особенности ведения данного урока в условиях ФГОС и проблемы, возникающие при рассмотрении данной темы.
Ключевые слова: профилизация обучения, современный урок, урок открытия нового знания, функция, производная, первообразная, неопределённый интеграл.
В связи с изменениями парадигмы образования современное общество ставит перед школой задачу профилизации будущих выпускников. Главной целью профильного обучения для учащихся является обеспечение общедоступности получения полноценного образования в соответствии с их индивидуальными склонностями и потребностями, обеспечение профессиональной ориентации и самоопределения обучающихся, установление преемственности между общим и профессиональным образованием [2].
Изменения также коснулись и требований, предъявляемых к школьному уроку. Возьмём, например, урок открытия нового знания. В условиях деятельностного подхода, данный урок подразумевает в себе не просто подачу материала как это было раньше, а создание условий для самостоятельного изучения.
Образовательная цель урока открытия нового знания в соответствии с ФГОС состоит или в выявлении учеником субъективно новых для него знаний, или в овладении новым содержанием на определённом уровне, в преобразовании нового теоретического знания в способы деятельности. Определение же развивающих и воспитательных аспектов целей вызывает у учителей ряд трудностей.
Заметим, что новые знания включают в себя не только информационный компонент, который явно отражён в школьном учебнике, но и методологические знания, познавательные средства. Одновременно с формулировкой определений или описанием понятий, теорем и их доказательства, правил ученик должен усваивать методы и способы их получения, осознавать, что математика в целом является методом познания реального мира.
Например, приступая к изучению первообразной следует после того, как у ученика уже сформированы следующие методологические знания: определение понятия производной, производные элементарных функций, суммы, разности, произведения, правила нахождения производных, применение производных (задачи на максимум и минимум).
В условиях современного урока обучение предполагает самостоятельную учебную деятельность от ученика. С точки зрения современной дидактики самостоятельной работой признаётся не только, когда ученик работает без учителя, но и, когда в ходе познавательной деятельности, осуществляется взаимодействие с коллективом, под руководством учителя, в ключе «учитель — ученик». Ключевым механизмом создания условий для самостоятельной деятельности учащихся на уроке является учебная задача, которую ученик должен принять как значимую для себя, которая должна заинтересовать его и побудить в нём желание решать её. Уровень самостоятельности учащихся будет у каждого свой, но самое главное, чтобы каждый ученик стал соучастником получения для него нового знания, осознавал и понимал свой вклад постановку и решение учебной задачи.
Каждое новое открытие предполагает формулировку проблемы (в нашем случае — в форме учебной задачи), поиска её решения и решение. А это в свою очередь, требует от учащихся, во-первых, овладения необходимой базой знаний и умение ей оперировать, во-вторых, иметь опыт поисковой деятельности и владения её методами и способами, в-третьих, личностной потребности и заинтересованности в её осуществлении.
Безусловно, система методологических знаний не зависит только от урока открытия нового знания, но по большей части знакомятся учащиеся впервые именно на этих уроках, все это вместе создает условия для достижения образовательной, развивающей и воспитательной целей урока.
Рассмотрим урок открытия нового знания, на примере «Первообразной (неопределённого интеграла)». Изучение раздела начинается на уроках математики в старших классах и рассматривается в такой дисциплине, как алгебра и начала математического анализа.
Формирование умения находить первообразную является важным аспектом при изучении алгебры и начала анализа. В настоящее время старшеклассники сдают ЕГЭ, где умение находить первообразную, посредством решения интеграла может способствовать уменьшению трудностей в решении не только алгебраических заданий, но и геометрических. Поэтому необходимо, чтобы обучающиеся со старшей школы знали азы как самой первообразной, так и всей алгебры в целом (функции и их графики, предел функции м непрерывность, обратные функции, производные, применение производных). Знания, умения и навыки решения интегральных функций, учащиеся приобретут в старшей школе изучая различные свойства, теоремы и формулы. Также не мало важную роль в процессе формирования умений играет учитель. Учитывая методические особенности той или иной темы, он сможет грамотно выстроить процесс обучения, в результате которого обучающиеся смогут лучше воспринимать полученный материал.
Однако, анализ опыта педагогической практики показывает, что проблемы по преподаванию данной темы, не уменьшаются. Знания школьников носят лишь формальный характер, а структура знаний отсутствует, не формируется представление о понятии неопределённый интеграл и не вырабатываются прочные навыки решения задач.
Причинами проблем и трудностей является очень высокая степень абстракции понятий, сложная логическая структура их определений, недостаточное время для осмысления и усвоения сложных вопросов и ряд других факторов. Поэтому успешное изучение раздела «Интеграл» зависит от необходимости решения проблем, связанных правильной постановкой целей изучения курса, тщательным отбором содержания теоретического и дидактического материалов и методическими приёмами, и особенностями [3, с. 198].
С дидактической точки зрения взаимообратные операции дифференцирования и интегрирования целесообразно рассматривать одновременно, поскольку решение взаимообратных задач позволит рассмотреть определения производной, как данной функции, так и функции имеющей данную производную.
В связи с тем, что понятие первообразной функции и понятие неопределённого интеграла, как совокупности первообразных вводятся позже в связи с изучением производной, будет разумно в простых случаях решать и обратную задачу, но при этом не пользоваться специальной терминологией и символикой. Это послужит пропедевтикой для введения понятия интеграла в явном виде. Так, после ознакомления с производного многочлена учащиеся могут не только отыскать производную по заданному многочлену, но и по производной находить функцию. [5, с. 322]
Прежде чем вводить понятие неопределённого интеграла, учащихся необходимо познакомить с понятием первообразной функции. Для этого на наш взгляд целесообразно начать изучение данной темы с рассмотрения таблицы производных функций. Здесь перед учащимися необходимо поставить следующую задачу: отыскать функции, производная которой равна данной (взятой из столбца производных)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дальнейшее развитие этой задачи: найти функции, производные которых равны
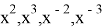
Данная задача, поставленная перед учащимися, решается неоднозначно: для каждой функции найдётся бесконечное множество функций, производная которых равна данной функции; эти функции отличаются только одной постоянной. Например,
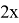
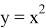
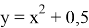
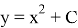
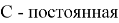
После подобных упражнений вводится определение первообразной функции или просто первообразной: «Функция
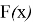
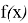
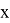
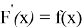
В большинстве приведённых примеров промежутком, в котором функции определены, является вся числовая прямая, найденные первообразные для них тоже определены на всей числовой прямой; в примерах 5, 6 и примере 7
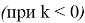
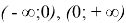
Использованную нами таблицу можно теперь переписать так, чтобы по ней удобно было находить первообразные данных функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На первых уроках на наш взгляд необходима проверка правильности решения задачи дифференцированием для закрепления понятия первообразной и для ликвидации вероятных ошибок: первое время учащиеся путают формулы дифференцирования и интегрирования.
Далее доказываются следующие теоремы.
1) Если
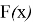
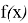
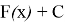
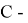
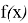
2) Если
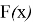
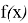
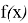
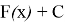
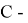
Таким образом, выражение
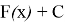
После доказательства этих теорем могут быть решены задачи, подобные задачам в таблице, и некоторые задачи физического содержания, например: «Скорость тела как функция времени задана формулой
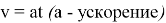
Такого рода задачи могут и предшествовать введению понятия первообразной, демонстрирую необходимость этого понятия для решения задач прикладной направленности. Но необходимо понимать, что при этом физическое содержание задач должно быть максимально прозрачным, чтобы не перекрывать сущность математического вопроса.
Что же касается введения понятия неопределённого интеграла и символа
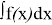
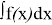
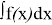
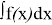
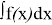
Литература:
- Иванова Т. А., Современный урок математики: теория, технология, практика: Книга для учителя. / Т. А. Иванова. — Н. Новгород: НГПУ, 2010. — 288 с.
- Концепция профильного обучения на старшей ступени общего образования // Официальные документы в образовании. 2002. № 27. С. 13–33.
- Марчук Н. А. Методические особенности преподавания темы «Интеграл» [Текст] / Н. А. Марчук, Н. К. Гульманов, А. А. Асетов // International scientific review / ООО «Олимп». — Иваново, 2016. — № 3. — С. 197–201.
- Мишин В. И. Методика преподавания математики в средней школе: частная методика: учебное пособие для студентов педагогических институтов по физико-математической специальности. / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и др.; Сост. В. И. Мишин. — М.: Просвещение, 1987. — 416 с.
- Столяр А. А. Педагогика математики: учебное пособие для студентов физико-математических факультетов педагогических вузов. / А. А, Столяр. — Минск: Вышэйшая школа, 1986. — 414 с.