В статье предложен метод для оптимизации реклоузеров в распределительных сетях. Данный метод позволяет обеспечить компромисс между эффективностью защиты и качеством электрической энергии.
Ключевые слова: качество электрической энергии, реклоузер, АПВ, надежность.
The article proposes a method for optimizing reclosers in distribution networks. This method allows for a compromise between the efficiency of protection and the quality of electrical energy.
Keywords: quality of electrical energy, recloser, automatic reclosing, reliability.
- Предложенный метод
Основная цель предлагаемого подхода состоит в том, чтобы минимизировать общие затраты на отключение из-за повторного включения, а также найти баланс между кратковременными и длительными отключениями. Оптимальная настройка реклоузера включает параметры стохастического характера, такие как место возникновения, тип, сопротивление и характер короткого замыкания. Чтобы учесть неопределенности метода Монте-Карло, в предлагаемом методе используется вычислительный алгоритм, основанный на повторной случайной выборке для получения численных результатов.
- Сначала в качестве настроек реклоузера выбирается одна из возможных интервалов повторного включения и количество циклов АПВ.
- Короткие замыкания со случайными характеристиками генерируются с учетом следующих моментов:
а) Место возникновения короткого замыкания;
б) Устойчивость к короткому замыканию;
в) Тип короткого замыкания;
г) Характер короткого замыкания;
- Затраты на неустойчивые и устойчивые короткие замыкания рассчитывается как:
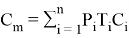
Где
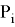
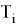
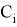
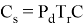
Где
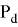
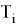
- Пример использования
Однолинейная схема исследуемой системы изображена на рисунке 1. В этой сети для защиты боковых линий использовались предохранители, а на подстанции был установлен реклоузер. Таблица 1 и таблица 2 показывают параметры линии и данные нагрузки. Рассмотрены следующие четыре возможных настройки реклоузера: 1 — два цикла АПВ с интервалом 1,5 секунды, 2 — один цикл АПВ с интервалом 1,5 секунды, 3 — два цикла АПВ с интервалом 0,5 секунды, 4 — один цикл АПВ с интервалом 0,5 секунды.
Общее количество отказов в этой сети считается как 15 отказов в год, а вероятности возникновения различных типов КЗ следующие: З(1) = 75 %, З(1+1) = 17 %, К(3з) = 3 %, К(2) = 3 % и К(3) = 2. %. Кроме того, 80 % коротких замыканий в этой сети являются неустойчивыми. В таблице 3 представлен процент неустойчивых КЗ, которые устраняются при каждом цикле срабатывания АПВ в соответствии с интервалом повторного включения. Сопротивление короткого замыкания имеет нормальное распределение со средним значением 5 Ом и стандартным отклонением 1 Ом. Путем изменения количества циклов, интервала повторного включения и повторения предложенного метода Монте-Карло выбирается третья настройка реклоузера в качестве оптимальной настройки для реклоузера в тестовой системе.
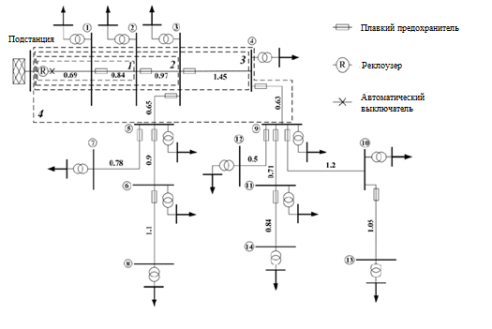
Рис. 1.Схема тестовой системы. Возможные зоны защиты показаны цифрами от 1 до 4. Длины линий указаны в километрах
Таблица 1
Параметры линии
|
Параметры линии |
Удельное сопротивление (Ом / км) |
|
Активное сопротивление (R) |
0.45 |
|
Индуктивное сопротивление (X) |
0.36 |
Таблица 2
Активная и реактивная мощность нагрузки.
|
Номер нагрузки |
P ( МВт ) |
Q (МВАр ) |
Номер нагрузки |
P ( МВт ) |
Q ( МВАр ) |
|
1 |
0.6 |
0.25 |
8 |
0.6 |
0.25 |
|
2 |
0.65 |
0.5 |
9 |
0.35 |
0.09 |
|
3 |
0.55 |
0.38 |
10 |
0.45 |
0.15 |
|
4 |
0.65 |
0.5 |
11 |
0.35 |
0.09 |
|
5 |
0.32 |
0.15 |
12 |
0.56 |
0.24 |
|
6 |
0.35 |
0.09 |
13 |
0.56 |
0.24 |
|
7 |
0.56 |
0.24 |
14 |
0.35 |
0.09 |
Таблица 3
Вероятность устранения короткого замыкания при каждом срабатывании АПВ
|
Интервал АПВ ( с ) |
Один интервал АПВ |
Два интервала АПВ |
|
|
Вероятность устранения при первом срабатывании (%) |
Вероятность устранения при втором срабатывании (%) |
||
|
Вероятность устранения (%) |
|||
|
0.8 |
80 |
50 |
10 |
|
1.5 |
80 |
80 |
15 |
- Заключение
В данной статье был рассмотрен метод Монте-Карло для оптимизации реклоузеров в распределительных сетях. В этом методе определены оптимальное количество операций, интервалы повторного включения и зоны защиты. Результаты моделирования подтверждают эффективность предложенного метода.
Литература:
- Chitsazan M. A. “Harmonic Mitigation in Interphase Power Controllers Using Passive Filter-Based Phase Shifting Transformer”/ M. A. Chitsazan, A. M Trzynadlowski. — М: Energy Conversion Congress and Exposition (ECCE), 2016. — pp. 1–5.
- Jalilzadeh Hamidi R. “A travelling wave-based fault location method for hybrid three-terminal circuits”/ R. Jalilzadeh Hamidi and H. Livani. — М: IEEE PES-GM, 2015. — pp. 1–5.
- Gers, J. M., and Holmes, E. J. “Protection of electricity distribution networks”/ J. M. Gers, and E. J. Holmes. — М: IET Press, 1998.







