Говоря сегодня о сжатии данных, на ум приходит вопрос: а нужно ли оно в наше время? Конечно же, да! Мы знаем, что сейчас нам доступны носители огромного объема и высокоскоростные каналы передачи данных, но нужно учитывать то, что объем передаваемой информации тоже растет. Если раньше мы смотрели фильмы невысокого качества, умещающиеся на одной болванке, то сейчас фильмы качества HD могут занимать десятки гигабайт. Разумеется, для хранения, и тем более передачи, информации такого объема понадобится много места и времени. Именно для таких случаев и используют метод сжатия данных. В нашей статье мы попытаемся понять, как работает сжатие данных без потерь, и рассмотрим самый распространенный метод сжатия без потерь — алгоритм Хаффмана.
Ключевые слова: данные, информация, сжатие данных, алгоритм Хаффмана, сжатие данных без потерь.
Сжатие данных — это алгоритмический процесс уменьшения объема данных путем сокращения их избыточности. Сжатие файла — это его уменьшение при сохранении исходных данных. [1] Существует два метода сжатия: с потерями и без потерь. При сжатии с потерями восстановленные данные несколько отличаются от исходных, например: разрешением, качеством звука и т. д.. Используют этот метод при сжатии изображений, аудио и медиа файлов, когда нет необходимости точного восстановления данных. При сжатии без потерь исходные данные восстанавливаются с точностью до бита. Такой способ используют для хранения и передачи текстовых документов, компьютерных программ. Далее мы будем рассматривать именно второй способ. [2]
Сжатие без потерь (СБП) уменьшает биты путем выявления и устранения статистической избыточности. Рассмотрим следующий пример, чтобы понять принцип работы этого метода. [4] На рисунке ниже изображено девять овалов- три бордовых, три зелёных, три желтых:

Вместо того, чтобы показывать все девять овалов, мы можем убрать все овалы, оставив по одному овалу разного цвета, и указав на них цифрами сколько было этих овалов вначале. То есть мы показываем те же данные, но используя меньшее количество фигур:

Оба рисунка несут в себе один и тот же смысл, содержат одну информацию, но на втором рисунке информация сжата, при хранении и передаче занимает меньше места.
Другой пример: возьмем файл, который хранит следующую информацию-
DDDDDDDDDDDYYYYYYFFFFFFFFFFFFFFFFFFFOOO. Этот текст мы можем сжать следующим образом: D11Y6F19O3. Таким образом вместо 39 символов, мы использовали 11 для представления тех же данных.
На первый взгляд, принцип сжатия данных выглядит слишком идеально, чтобы быть правдивым. Идея сокращения информации без потери ее части смотрится как бесплатное предложение, которое должно бы нарушить один малоизвестный закон Ньютона: закон сохранения данных.
Несмотря на окружающую мистическую ауру, сжатие данных основано на простой идее: отображение представления данных из одной группы символов на другую, более компактную серию символов. Чтобы достигнуть этого, программы сжатия данных и соответствующая аппаратура используют несколько различных алгоритмов, самыми основными из которых являются метод Хаффмана и LZW- кодирование. [6]
Алгоритм Хаффмана
Простота и легкость данного способа сжатия информации сделали его популярным среди пользователей. Хотя он и был создан в далеком 1952 году, но даже в наше время этот метод остается актуальным. Кодирование Хаффмана работает на принципе того, что есть вероятность, что некоторые символы в представлении данных используются чаще, чем другие. Суть алгоритма в том, чтобы найти символы с большей частотой и дать им самый короткий код, а символам с наименьшей частотой дать самый длинный код. На входе в алгоритме Хаффмана должна быть уже задана таблица частот, без нее кодирование невозможно. [2]
Алгоритм
- Задается таблица частот;
- Выбираются два узла с наименьшим весом (частотой);
- Создается родитель равный весу их суммы;
- Родитель — это новый свободный узел, а те два узла-потомка удаляются;
- Для дуги, выходящей из родителя, ставится в соответствие бит 1 или 0;
- Вся эта операция повторяется, пока в списке не останется единственный узел.
Приведем пример. Нам задана следующая таблица частот:
|
F |
G |
H |
J |
|
10 |
3 |
7 |
18 |
Согласно нашему алгоритму, мы должны суммировать два узла с наименьшей частотой: G+ H= 3+ 7= 10. Из G и H получается новый родитель G/H, вес которого составляет 10, а эти узлы удаляются. На следующем шаге наименьший вес у узлов G/H и F. Получается новый родитель с весом 20, а эти узлы удаляются. Это операция происходит, пока не останется один единственный узел.
Дерево кодирования выглядит так:
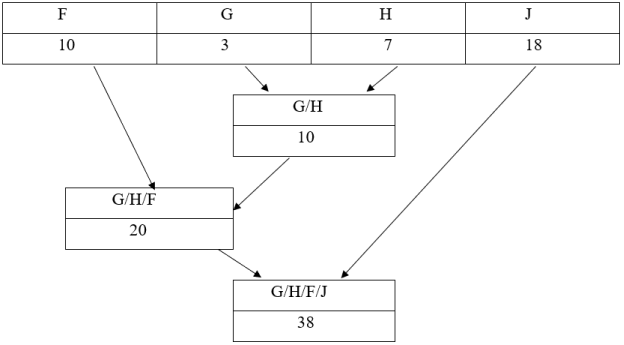
Далее нам нужно задать код для каждого символа. Для этого мы будем двигаться снизу-вверх по нашему дереву до корня, накапливая биты при перемещении по ветвям. Перемещение вправо — 0 бит, влево- 1 бит. У нас получится следующая таблица:
|
F |
G |
H |
J |
|
11 |
101 |
100 |
0 |
Как нам и обещал алгоритм символ с наибольшей частотой получил меньший код (J= 0= 0), а символ с наименьшей частотой наибольший код (G= 101= 5).
Классический алгоритм Хаффмана имеет один существенный недостаток. Для восстановления содержимого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что приводит к увеличению размеров выходного файла. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и дерева), другого для собственно кодирования. [5]
В этой статье мы с вами подробно описали один из видов сжатия данных -сжатие без потерь, и самый популярный алгоритм этого метода — кодирование Хаффмана. Естественно, это не единственный алгоритм сжатия данных, их очень много, и какой метод выбрать решает сам пользователь. Сегодня, в век информации, несмотря на то, что есть носители огромного объема, проблема сжатия данных все еще остается актуальной.
Литература:
- Баринов В. В. Сжатие данных, речи, звука и изображений в телекоммуникационных системах; РадиоСофт — Москва, 2009. — 360 c.
- Вотолин Д. Ратушпяк А. Смирнов М. Юкин В. Методы сжатия данных. Устройство архиваторов, Сжатие изображений и видео. — М.:ДИАЛОГ-МИФИ, 2003 г. — 381 с..
- Рассел Джесси Сжатие данных; Книга по Требованию — Москва, 2013. — 104 c.
- Ратушняк О. А. Сжатие мультимедийной информации. // Hard'n'Soft. 2001. — №.4 — стр. 78–79.
- Сэломон Д. Сжатие данных, изображений и звука; Техносфера — Москва, 2006. — 368 c.
- Электронный ресурс: https://mf.grsu.by/UchProc/livak/po/comprsite/theory_contents.html







