В статье авторы показывают эффективность применения приёмов технологии критического мышления для формирования УУД учащихся.
Ключевые слова: рефлексия, критическое мышление.
Школа должна не только формировать у учащихся прочную основу знаний, умений и навыков, но и максимально развивать их критическое мышление: учить мыслить, самостоятельно обновлять и пополнять знания, сознательно использовать их при решении теоретических и практических задач. Активная, самостоятельная работа мысли начинается только тогда, когда перед учащимися возникает проблема, вопрос. Поэтому самое важное — создать условия для постановки учащимися собственных целей обучения, помочь им в определении маршрута для их достижения и посредством разнообразных стратегий, методов и приёмов сопровождать учеников по выбранному маршруту. Изучение темы (а значит, и сам технологический цикл) может занимать несколько уроков, при этом стадии могут повторяться неоднократно [1, с. 7]. В подтверждение сказанному, рассматриваются два урока по изучению темы: «Положительные и отрицательные числа. Координатная прямая» в 6 классах.
Урок 1. Урок начинается с проведения небольшой физ. минутки, которая поможет укрепить учащихся не только физически, но умственно, а также проверить их внимательность и находчивость. Ученики получают по карточке с изображением одного из знаков действий «+», «-» и числа 0. Ученики, получившие карточку с изображением «+» называют воздушный вид транспорта и поднимают руки верхи, становятся на носочки. Кому досталась карточка с изображение числа нуль, называют наземный вид транспорта и вытягивают руки вперед. Ученики, получившие карточку с изображение «-» называют подводный и сгибают колени. Учитель просит учащихся посмотрите друг на друга и проанализировать их действия. Ученики ответили, что в первом случае (знак «+») они стали выше, во втором случае (число 0) не изменился рост, а в третьем (знак «-») они стали ниже. Этот прием позволил поделить учащихся на группы. На стадии Вызова использовали прием «Мозговой штурм», где учащимся предлагалось задание по распределению чисел по группам, которое помогло им определить тему урока. На стадии Осмысления работали с информационным текстом учебника.
Задание1. Дайте определения положительных чисел, отрицательных чисел. Число нуль будет ли являться положительным или отрицательным числом? (работа с учебником). К какому числу можно отнести изменение вашего роста (увеличение, уменьшение, отсутствие изменений) на физ. минутке?
Задание 2. Представление информации по теме «Положительные и отрицательные числа» в кластерах. Одна из групп должна была привести примеры записи значения величин положительным числом, вторая группа-запись значения величин отрицательными числами и третья группа — запись значения величин нулем.
Изучая самостоятельно тему «Координатная прямая» учащиеся заполняли таблицу «Знаю — хочу узнать — узнал» . На стадии рефлексии, учащиеся выполнили проверочную работу с последующей самопроверкой. В конце урока заполнили рефлексивные листы (продолжить начало фразы):
сегодня я узнал…
было интересно…
было трудно…
теперь я могу…
В результате обратной связи, было выяснено, что большая часть учеников класса успешно справились с работой.

Рис. 1
Урок 2
Урок был построен на основе «Технология развития критического мышления» использованы такой прием, как: «мозговой штурм», индивидуальная работа, в парах и групповая работа. В течение урока выдерживалась модель Вызов — Осмысление — Рефлексия.
На стадии Вызова использовался метод «Мозаика» для деления класса на группы. Каждый ученик, получивший карточку, сначала ознакомился с её содержимым, а затем начал находить в классе тех учеников, которые имеют примеры, относящиеся к данным понятиям (положительному числу, отрицательному или числу нуль). Был использован прием устного опроса «Светофор» . Использую технику «Светофор», суть которой заключается в том, что у каждого ученика имеются карточки трех цветов светофора, одну из которых они поднимают, обозначающие их полное понимание, частичное понимание или непонимание материала. По итогам полученных ответов учитель принимает решение о повторном изучении, закреплении темы или продолжении изучения материала по программе [4, с. 19]. Учащиеся обобщили имеющиеся знания и в ходе выполнения и обсуждения результатов, выявили недостаточность имеющихся знаний. Следующий прием формативного оценивания уровня понимания учащихся — «Проверка ошибочности понимания», виде игры «Вверю, не верю», где намеренно даются учащимся типичные ошибочные понятия или предсказуемые ошибочные суждения о каких-либо идеях, принципах или процессе и понятиях. Затем просят учащихся высказать свое согласие или несогласие со сказанным и объяснить свою точку зрения [4, с. 21].

Рис. 2
На стадии Осмысления были использованы элементы приёмов «Ромашка Блума», вопросы связаны с классификацией уровней познавательной деятельности: знание, понимание, применение, анализ, синтез и оценка.
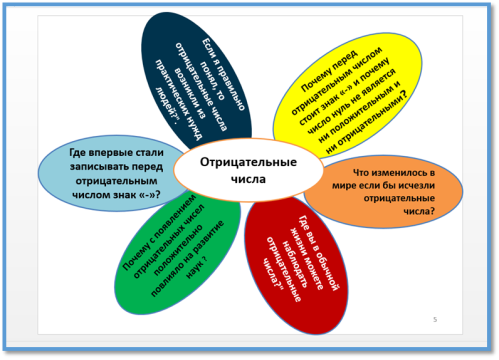
Рис. 3
Учащимся тяжело довались ответы на вопросы связанные с анализом и синтезом, много времени ушло на поиски ответов.
Использовался метод « Развивающийся канон ». Суть этого метода заключается в том, что даются три слова, первые два находятся в определенных отношениях. Найди четвертое слово, чтобы оно с третьим было в таких же отношениях.

Рис. 4
На стадии рефлексии учащиеся самостоятельно оценили процесс выполнения ими работ. Провели самооценку. Для того чтобы учащиеся смогли оценить свои знания по данной теме, были разработаны критерии оценки.

Рис. 5
Благодаря использованию данных технологий, в процесс урока были вовлечены все учащиеся.
Математика складывалась в науку индуктивным путём, т. е. от частного к общему, а изучается эта наука обратным методом: от общего к частному. Каждый из этих методов занимает своё определённое место в образовательном процессе. Необходимо напоминать детям, что математика возникла из практических нужд людей и многие знания были получены эмпирическим путём. Но выводы, которые мы поспешно делаем, пользуясь индуктивным методом, могут оказаться ошибочными, то есть индуктивный метод не может гарантировать всегда достоверный вывод. В 6 классе при изучении темы простых чисел привожу пример из истории, когда французский математик Пьер Ферма утверждал, что выражение 2 2 n + 1 при любом положительном и целом n обращается в простое число. При n= 0,1,2,3,4 получаются простые числа, но при n=5 получаем число 4 294 967 297, которое является составным, т. к. делится на 641 без остатка. Ошибочное заключение, сделанное Ферма, обнаружено великим математиком Эйлером, членом Петербургской Академии наук. Под влиянием индуктивного метода впадали в ошибку даже крупнейшие учёные.
Эффективность учебной деятельности по развитию критического мышления во многом зависит от творческой активности учащихся при решении геометрических задач. Перед изучением теоремы Пифагора практическим путём устанавливаем данную закономерность на нескольких треугольниках. Но можно ли на основании этих вычислений утверждать, что она справедлива для любого треугольника? После этого переходим к строгому доказательству теоремы, идя от известного к неизвестному, то есть пользуясь более надёжным, дедуктивным методом.
Так в начале изучения стереометрии, учащиеся с трудом воспринимают и выполняют чертеж пространственной фигуры. Поэтому с первых уроков геометрии в 10 классе идёт целенаправленное формирование у учащихся навыков восприятия чертежа. Для этого одни и те же задачи одновременно решаются по рисунку и модели. Модели параллелепипеда, куба, тетраэдра я ввожу с первых уроков. И после изучения аксиом стереометрии и их следствий учащиеся строят сечения плоскостей, пересекающие пирамиду, куб, параллелепипед, тетраэдр. Далее обучающиеся строят сечения, применяя параллельность прямых и плоскостей. Построение сечений в начале изучения стереометрии дают возможность учащимся закрепить аксиомы стереометрии и их следствия, параллельность прямых и плоскостей, формировать пространственные представления, что не мало важно для дальнейшего изучения стереометрии, решении задач, сдачи зачётов.
А вот в 5- 6 классах большее внимание уделить практической направленности, т. к. трудности вызывают запоминание формул периметра, площади прямоугольника и квадрата, площади поверхности и объёма прямоугольного параллелепипеда.
Задачи и упражнения в отыскании ошибок также играют значительную роль в развитии критического мышления учащихся. К таким задачам относятся софизмы — суждения, в которых неправильные или ложные предпосылки выдаются за истинные, в результате чего мы приходим к нелепым умозаключениям. Педагогическая ценность будет достигнута только тогда, когда учащиеся совершенно отчётливо поймут, в чём именно заключалась допущенная в софизме ошибка и как её надо исправить. Примеры софизмов:
1) Докажем, что 2=3;
2) Четверть больше половины;
3) В каждом прямоугольном треугольнике катет равен гипотенузе;
4) косинус угла больше единицы.
В 6 классе обратить внимание на решение странного уравнения:
15х — 30 = 12х -24. Вынесем в обеих частя уравнения общий множитель за скобку:
15(х — 2) = 12(х -2)
Разделив обе части на х -2, получим, что 15 =12! Предлагается ученикам разобрать данный софизм. Решить уравнение обычным приёмом без вынесения общего множителя. Получим х=2. То есть ошибка заключалась в делении обеих частей уравнения на нуль.
В 10- 11 классе рассматриваем софизм: Доказать, что cos a> 1.
Допустим, что 0< a<п/2,
cosa = cosa
Тогда, lg cosa= lg cosa
Cледовательно, 2 lg cosa> lg cosa
или lg cos^2 a> lg cosa
Откуда, cos^2 a> cosa.
Разделив обе части на cosa (т. к. cosa >0),
получим, что cosa>1.
Ошибка допущена в выражении 2 lg cosa> lg cosa.
В действительности, 2 lg cosa < lg cosa.
Учащиеся должны это обосновать.
Школьные математические софизмы построены на типичных ошибках учащихся: деление на нуль, извлечение квадратного корня из отрицательного числа, незнание свойств логарифмов, некритическое отношение к чертежу. Поэтому разбор с учащимися софизмов ограждает их от повторения таких ошибок в будущем и надо находить время на решение подобных заданий.
Таким образом, технология развития критического мышления даёт учащимся возможность размышлять, классифицировать, оценивать, критически анализировать информацию, делать выводы. Умение учеников самостоятельно делать выбор и принимать решения, ведет к формированию самостоятельного человека, способного жить в современном обществе.
Литература:
- С. И. Заир-Бек, И. В. Муштавинская, Развитие критического мышления на уроке. Пособие для учителей общеобразовательных учреждений. Москва «Просвещение» 2011, 223 с.
- Е. В. Сергеева, М. Ю. Чандра, Современные технологии оценивания учебных достижений обучающихся. Учебное пособие — Волгоград Издательство ПРИНТ 2013, 115 с.
- Ирина Муштавинская: Технология развития критического мышления на уроке и в системе подготовки учителя. «КАРО», 2009, 84с.
- Р. Х. Шакиров, А. А. Буркитова, О. И. Дудкина, Оценивание учебных достижений учащихся. Методическое руководство — Бишкек «Билим», 2012г, 80 с.

