В статье автор описывает упражнения, способствующие формированию у младших школьников умения моделировать при решении задач с геометрическим содержанием
Ключевые слова: моделирование, текстовые задачи, геометрическое содержание.
Одним из основных умений, формируемых в начальной школе, согласно ФГОС НОО, является моделирование. Его активное формирование происходит в процессе решения текстовых задач с геометрическим содержанием. Усваивая зависимости между геометрическими величинами, описанные в задаче, активно развивается моделирующая деятельность.
Моделирование — деятельность, обеспечивающая формирование знаний о последовательности решения учебной задачи, умения кодировать информацию, использовать заместителей для ее представления, умений представлять информацию в самых разных видах [1].
На практике педагог упускает данное умение, требуя от ученика решение и ответ к задаче. Эта проблема приводит к тому, что младший школьник использует одну модель для задач разного уровня сложности, не понимая цель моделирующей деятельности. Серьезные трудности учащиеся испытывают при самостоятельном построении модели того или иного вида для поиска пути решения текстовых задач с геометрическим содержанием, в случае, когда текстовая конструкция задачи усложнена.
Чтобы эти трудности устранить, педагогу необходимо включать в уроки математики специальные задания, при выполнении которых учащиеся изучают, преобразовывают, создают модели разных видов, тем самым осознанно усваивают зависимости между величинами, входящими в задачу.
Проиллюстрируем на конкретных примерах, как педагог может организовать деятельность, направленную на формирования моделирования при решении задач с геометрическим содержанием.
Задание 1. «Выполни схематический рисунок и реши задачу. Ширина бассейна прямоугольной формы 10 м, длина на 11 м больше. Чему равен периметр и площадь бассейна?»
Предложенное задание ученики выполняли самостоятельно, затем осуществлялась проверка. После проверки решения задачи, классу был задан вопрос: «Какие знания вам помогли найти площадь; периметр?».
Необходимо обратить внимание на смысл отношений при составлении чертежа и показать другие варианты модели к текстовой ситуации. Для этого был задан вопрос: «Какую вы можете выполнить модель, чтобы показать смысл отношения?» Ученики предлагали различные способы построения модели, как схематический чертеж, схематический рисунок, таблица.
Задания такого типа способствовали пониманию и принятию учебной задачи; нахождению геометрических величин; преобразованию текстовой модели в схематические модели, на основе которой дети выстраивают этапы решения задач.
Следующее задание педагог может предложить учащимся с целью формирования моделирующей деятельности, как анализ представлений о разных видах моделей и выбора формы модели.
Задание 2. «Ширина стола прямоугольной формы равна 110 см, а его периметр 326 см. Чему равна длина стола?»
После прочтения данного задания, детям был задан вопрос: «Какие знания вам помогут в моделировании текста предложенного задания?» После обсуждения в парах учащимися предлагается составить две схематических модели. Затем ученик выходит к доске и предлагает вариант моделирования текста задачи, другой ученик — свой вариант. В результате были проанализированы виды моделирования. Каждый из учащихся выбрал определенный вариант моделирования, который удобен ему. Затем дети самостоятельно решили задание и проверили друг друга.
Текстовую ситуацию, описанную в задании, учащиеся изобразили:
в виде таблицы:
|
Длина, см. |
Ширина, см. |
Периметр, см. |
|
? |
110 |
326 |
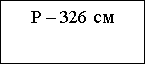
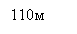
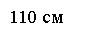
в виде краткой записи:
P — 326 м
Ш — 110 м
Д -?
С задачами простого уровня сложности учащиеся справляются успешно, а с задачами усложненного типа возникают трудности. Именно выстроить ход решения в таких задачах помогает моделирующая деятельность, но не стоит забывать, что она должна быть правильной.
Задание 3. «Выполни схематический чертеж и реши задачу. Длина участка прямоугольной формы на 10 см больше ширины. Вычисли площадь доски, если ее периметр равен 80 см».
Это самое распространенное задание, где на практике её решают несколько учащихся, потому что в условии известна одна величина. Данное задание учащиеся обсуждали в парах, а затем коллективно. Учащимися была предложена модель в виде ключевых слов.
Д. –?, на 10 см > Ш
Р. — 80 см.
S. –?
При обсуждении хода решения задачи возникли трудности. Тогда педагог предлагает выполнить модель другим способом. Учащиеся моделируют текст задачи в виде прямоугольника, потому что участок прямоугольной формы.

Пользуясь этой схемой, учащиеся снова затруднились в поиске решения задачи. Учитель, используя методический прием «Начало решения», выполнил 1-е действие решения: 1) 80:2=…
Рассуждение строится таким образом: «Периметр участка (сумма всех его сторон) поделили на две части, этим мы найдем дину и ширину». Значит, 80:2 = 40 (см) — длина и ширина участка. Следующее действие: 40–10 = 30 (см) — две ширины, потому что разница между длиной и шириной в 10 см. Зная две ширины, можно найти одну ширину: 30:2=15 (см). Если известна ширина, а она меньше длины на 10 см, то можем найти длину: 15+10=25 (см). Зная длину и ширину участка, мы можем найти площадь: 25*15=375 (кв. см)».
Также педагог может дать дополнительное задание, где предлагает решить задачу другим способом. При анализе процесса решения заданий разными способами учащиеся учатся анализировать, конструировать схематическое моделирование и преобразовывать модель, а также выбирать наиболее рациональный способ решения задачи.
На основе приведенных примеров решения геометрических задач, учащиеся изучают текстовые модели, прообразовывают ее в другие виды моделей (как ключевые слова, схематический чертеж). Прием «Начало решения» эффективен на практике, так как наталкивает учащихся на соотнесение модели с началом решения, что помогает выстроить ход решения задачи.
Такая работа приводит к тому, что наиболее эффективным видом моделирования при решении геометрических задач, является схематический чертеж, т. к. он в наглядной форме показывает отношения и значения геометрических понятий, поэтому младшему школьнику легче выстроить ход решения задания [2].
Таким образом, в начальной школе умение моделировать при решении текстовых задач с геометрическим содержанием будет протекать успешно, если педагог методически грамотно организует учебную деятельность, в результате которой учащиеся научатся использовать моделирование, позволяющее осознавать связи между геометрическими величинами, на основе которых производится выбор арифметического решения задачи.
Литература:
- Виноградова, Н. Ф. Формирование у младших школьников универсальных учебных действий / Н. Ф. Виноградова // Начальное образование. — 2015. — № 5. — С. 3–10.
- Стойлова, Л. П. Обучение решению задач и моделирование: сборник статей / Сост. Н. Б. Истомина, Г. Г. Шмырева. — Смоленск: Изд-во Ассоциация 21 век, 2005. — С. 140–149.







