В статье рассматриваются способы визуализации взрывов в современной компьютерной графике. Особое внимание уделяется системам частиц, как одному из методов моделирования и визуализации взрывов: описывается принцип работы этого метода и простейшая реализация программы, моделирующей и изображающей взрыв на его основе. Также рассматриваются способы увеличения реалистичности изображения взрыва на основе систем частиц, в частности, описывается концепция такого метода моделирования как гидродинамика сглаженных частиц.
Ключевые слова : компьютерная графика, взрывы, системы частиц, гидродинамика сглаженных частиц, SPH.
Визуализация взрывов является довольно нетривиальной задачей компьютерной графики. За всё время было создано огромное количество самых разных алгоритмов решения этой задачи, отличающиеся друг от друга самыми разными свойствами. Они отличаются друг от друга скоростью, сложностью, областью применения, требованиями к памяти и другими особенностями.
В данной работе будут рассмотрены способы, основанные на системе частиц. В начале будет рассмотрено само понятие системы частиц и способы его реализации. Затем, для примера, на основе системы частиц будет реализован простейший взрыв. После этого будут описаны различные физические модификации простой модели из частиц, для повышения реалистичности изображения.
Обзор основных методов
Есть 3 основных метода визуализации взрыва: наложение текстур, физическая модель и система частиц. Метод текстур заключается в том, чтобы изначально подготовить изображения взрыва или его части, а потом визуализировать их. Этот метод имеет очевидное преимущество в скорости, однако во многих случаях неприменим и требует предварительное создание такой текстуры, которое всё равно придётся делать другим методом. Второй метод основывается на симуляции физической модели взрыва и на её основе определении итогового изображения. Однако данный метод требует решения дифференциальных уравнений в частных производных, что сильно бьёт по производительности и непригодно для визуализации в реальном времени. Третий метод основан на представлении взрыва в виде множества других простых для визуализации объектов, которые в совокупности становятся похожими на взрыв. Этот метод наиболее часто используется для визуализации объектов, не имеющих чётких границ, так как он может быть довольно быстр и прост в реализации. Его недостаток в том, что такая модель не имеет ничего общего с реальной моделью взрыва, из-за чего нужное изображение не всегда может быть получено без использования каких-то других методов. [1]
Чаще всего используются комбинации различных методов. К примеру, центр взрыва, представленного системой частиц, может быть заменён текстурой для оптимизации. Или правила движения частиц могут быть рассчитаны исходя из приближённой физической модели взрыва. В свою очередь сами частицы в самом частом случае визуализируются при помощи текстур. Из-за всего этого грань между этими тремя основными методами стирается и появляется огромное разнообразие самых разных способов решения данной задачи.
Системы частиц
Объекты, не имеющие чётких границ, такие как дым, туман, облака, огонь, взрывы в компьютерной графике не могут быть представлены полигонами. Для их визуализации используются другие методы, одним из которых является система частиц. Система частиц — это набор из многих объектов, называемых частицами, которые все вместе образуют целевой объект. Обычно частицы представляют собой довольно простые для визуализации объекты: точки или небольшие полигональные модели. Однако бывают и усложнения, вплоть до того, что частицы сами являются системами частиц (такие системы частиц называются многоуровневыми). Понятие система частиц было придумано и впервые использовано в 1982 году. Этот метод был использован для создания спецэффекта для фильма «Звёздный путь 2: Гнев Хана». [2]
Каждая частица в системе имеет свои атрибуты, такие как координата, цвет, скорость, время жизни и многие другие. На протяжении времени частицы меняют своё состояние: они двигаются, у них может меняться цвет или текстура, они могут взаимодействовать с окружением и так далее. Редко бывает такое, чтобы какая-то частица не изменялась на протяжении своего существования. Частицы создаются в некоторой изначально заданной области, при этом место рождения обычно выбирается случайно из множества возможных (причём распределение может быть равномерным, а может быть более сложным). Такая область часто называется эмиттером. Частицы могут быть созданы все в один момент, могут создаваться некоторым количеством каждый кадр, а могут и создаваться с каким-то интервалом. При этом количество создаваемых частиц так же может выбираться случайно, руководствуясь средним значением и отклонением, либо как-то сложнее. Начальные характеристики, такие как направление движения, цвет, скорость и тому подобное также могут задаваться произвольным образом, руководствуясь изначально заданным законом распределения.
После создания частицы обычно уже не взаимодействуют друг с другом, а руководствуются параметрами, заданными при создании. К примеру: они могут двигаться с некоторой заданной при создании скоростью в направлении так же указанном при создании. Могут двигаться по какому-то другому закону, однако чаще всего этот закон определяется именно при создании. При этом в некоторых системах частицы всё-таки могут взаимодействовать, однако это взаимодействие сильно может уменьшать производительность, поэтому при их программировании стараются, чтобы все законы изменения были заданы изначально.
Также у частиц есть такая характеристика, как время жизни. Время жизни — это некоторое натуральное число, которое каждый кадр уменьшается на 1, и при достижении нуля частица умирает, то есть для неё перестаёт рассчитываться изменение, и она перестаёт отрисовываться. Время жизни так же задаётся при создании, и может быть фиксированным для всех частиц, а может выбираться случайно. Комбинация различных вариантов этих атрибутов и способов визуализации самих частиц даёт огромные возможности для реализации самых разных эффектов.
Простейшая реализация
Эмиттером в системе частиц, моделирующей взрыв, является его центр. Частицы одномоментно создаются и разлетаются в разных направлениях. Закон их движения может быть совершенно различным, в зависимости от того, что нужно получить в итоговом изображении. Далее будет рассмотрено создание системы частиц и простейшего взрыва на её основе. Целью данной реализации не будет создание реалистичного взрыва, а лишь рассмотрение методик, использующихся для него.
В описываемой реализации каждая частица имеет такие характеристики, как координаты x и y, время жизни, скорость (координата x и y вектора скорости). Законом движения для простоты является простое равномерное прямолинейное движение. Для создания эффекта наложения цвета используется аддитивное смешивание: интенсивность красной, зелёной, синей и альфа компоненты двух точек, попадающих на один пиксель, накладываются. Таким образом, чтобы край взрыва был красным, внутренность жёлтая, а центр белый, цвет частицы должен иметь максимальную интенсивность красной компоненты, небольшую зелёную и очень маленькую синюю. Был выбран цвет с красной, зелёной, синей и альфа компонентой соответственно 1.f, 0.2f, 0.035f, 0.15f.
В функцию инициализации системы частиц передаётся координаты центра, среднее количество частиц, линейное отклонение количества частиц, среднее время жизни, его линейное отклонение и максимальная скорость частиц. Реальное количество частиц считается по формуле:
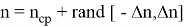
где n — количество частиц, n ср — среднее количество частиц, Δn — линейное отклонение количества частиц, rand [ x , y ] — случайное число из отрезка [ x , y ]. Функция инициализации создаёт нужное количество частиц, присваивая их атрибутам следующие значения: координаты x, y инициализирует значениями координат центра взрыва, время жизни по среднему времени жизни и линейному отклонению рассчитывается аналогично количеству частиц, скорость же частиц рассчитывается по чуть более сложной формуле. Угол между вектором скорости и осью x берётся случайным из множества всех возможных значений углов (от 0 до 2π, включая 0). Модуль скорости рассчитывается при помощи функции Гаусса:
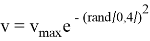
где v — модуль скорости, v max — максимальный модуль скорости, rand [0, 2] — случайное число из отрезка [0, 2]. Затем координаты x и y скорости рассчитываются через эти величины с помощью стандартных формул аналитической геометрии. Также, для уменьшения зернистости картинки, желательно сделать так, чтобы у частиц с меньшей скоростью время жизни было больше. В данной реализации это решается простым прибавлением к времени жизни умноженной на 60 разности максимальной скорости и скорости данной частицы.
Состояние всех частиц в системе периодически обновляется. В данной реализации это будет происходить 60 раз в секунду. Каждое обновление состояния уничтожаются частицы со временем жизни 0, вычитается 1 из времени жизни, а к координатам прибавляется соответствующая компонента скорости. Расчёт состояния сводится к самым простейшим преобразованиям, из-за чего он выполняется достаточно быстро.
Отрисовка каждой частицы может выполняться различными способами. Альфа компонента цвета каждой частицы должна зависеть от её оставшегося времени жизни: чем его меньше, тем меньше яркость. Это необходимо для эффекта затухания частицы, чтобы частицы не пропадали неожиданно, а постепенно затухали.
Для визуализации отдельных частиц обычно используют простую отрисовку текстуры. Текстурой частиц взрыва должен стать круг такой, что в каждой его точке компоненты цвета R, G, B и A равны и их интенсивность уменьшается при отдалении от центра круга. Для расчёта такой текстуры будет использована функция Гаусса:
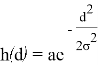
где h — интенсивность цвета, d — расстояние до центра круга, a — интенсивность цвета в центре круга, σ — стандартное отклонение. Различным выбором величин a и σ можно получать текстуры различных размеров и интенсивностей цветов. На рисунке 1 показан результат при a = 255, σ = 128.
Результат работы этой программы с 50000 частиц, максимальной скоростью равной 0.3 и временем жизни 300 показан на рисунках 2 и 3: на 2 изображено распространение взрыва, на 3 его затухание.
Сложность в визуализации трёхмерного взрыва заключается в визуализации самих частиц. Для их отрисовки обычно применяют технологию billboarding: текстуры, всегда повёрнутые к зрителю. Таким образом, всё отличие трёхмерного случая в появлении ещё одной координаты.

Рис. 1

Рис. 2

Рис. 3
В рассматриваемой реализации поворот камеры не предусмотрен вообще, поэтому никаких дополнительных расчётов проводить не нужно. Если бы это было не так, то пришлось бы в функцию отрисовки каждой частицы передавать координаты наблюдателя, чтобы та рассчитала плоскость, перпендикулярную к прямой, проходящей через наблюдателя и частицу, и отрисовала необходимую текстуру на ней.
На рисунке 4 изображено распространение трёхмерного взрыва, на рисунке 5 его затухание. Как и следовало ожидать, на первый взгляд изображение не слишком отличается от двухмерного случая. Однако при детальном рассмотрении различия заметны и полностью эти различия проявляются при наличии в сцене других трёхмерных объектов.

Рис. 4

Рис. 5
Способы повышения реалистичности
Система частиц является довольно мощным инструментом компьютерной графики. С её помощью можно создать изображение практически любого объекта, не имеющего чётких границ. Однако это требует от программиста мастерства, так как зачастую бывает не так просто придумать начальные значения так, чтобы получалось нужное изображение. Модели, более приближенные к реальному взрыву, имеют куда более сложные правила обновления состояния частиц и их рассмотрение не входит в цель данной работы.
Чем более реалистично изображение взрыва, тем больше частиц оно требует. Самые реалистичные реализации требуют колоссального количества частиц. Такие реализации требуют слишком много ресурсов для обработки обновления состояния системы, а значит, и времени, из-за чего они непригодны для визуализации в реальном времени. Однако, если целью является не моментальный расчёт картинки и немедленный её вывод, а сама итоговая картинка, без необходимости её получения в ближайшем времени, то такой способ вполне может сгодиться. Таким способом активно пользуются для визуализации спецэффектов в фильмах или для создания полностью анимационных фильмов. Именно поэтому в фильмах картинка красивее, чем в играх: в фильмах она может рассчитываться и визуализироваться часами, в то время как в играх она должна быть рассчитана и визуализирована немедленно. [3]
Если поставить задачей визуализацию как можно более приближенного к реальному изображения взрыва, то совсем без физической модели не обойтись. Распространение взрыва, изменение плотности дыма, и другие важные для визуализации характеристики — всё это изменяется по совсем нетривиальным законам. Конечно, эти законы физике известны, и можно с довольно большой степенью точности рассчитать необходимые величины, однако это требует довольно сложных вычислений и не годится для графики реального времени. Поэтому было придумано довольно много различных моделей, которые хоть и не с идеальной точностью, но дают картинку очень похожую на реальную и требуют не таких сложных вычислений.
SPH как метод моделирования взрывов
Одним из методов приближённого моделирования взрывов является гидродинамика сглаженных частиц (Smoothed particle hydrodynamics, SPH). Этот метод используется для моделирования жидкостей и газов. Его идея очень похожа на идею системы частиц: представление сложного непрерывного объекта в виде множества более простых объектов. Газ делится на частицы с определённым размером, называемым длиной сглаживания. Все пространственные величины для частиц сглаживаются, посредством свёртки с некоторым ядром сглаживания:
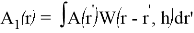
где A — пространственная величина, сглаживание которой происходит, A 1 — сглаженная величина, r — местоположение частицы, h — длина сглаживания, W — ядро сглаживания. Таким образом частицам приписывается значение любой пространственной величины. При необходимости значение в определённой точке r вычисляется так:
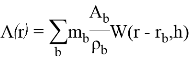
где A — значение искомой величины, суммирование происходит по всем частицам, m b — масса b -й частицы, A b — значение искомой величины у b -й частицы, ρ b — плотность b -й частицы, r b — местоположение b -й частицы, W — ядро сглаживания, h — длина сглаживания. [4]
Модель сглаженных частиц позволяет очень сильно уменьшить вычислительную сложность, так как в ней уравнения в частных производных трансформируются в обыкновенные, которые решаются гораздо проще. При этом, погрешность уменьшается при увеличении количества частиц, и таким образом, при достаточном количестве частиц она является приемлемой. [5] При этом данная модель не требует изобретения нового способа визуализации, позволяя использовать уже рассмотренную систему частиц.
SPH далеко не единственная модель, основанная на физических законах и использующая для визуализации систему частиц. Существует много других моделей, некоторые из которых являются модификацией SPH, а некоторые вообще не имеют с ней ничего общего. Однако их перечисление и описание выходит за рамки данной работы, поэтому они будут лишь упомянуты.
Заключение
Таким образом, в современной компьютерной графике система частиц является самым используемым способом визуализации взрывов. Различные возможности модификации системы частиц позволяют использовать её для отрисовки самых разных взрывов: от совсем простых до наиболее реалистичных, основанных на физических моделях. Большинство методов визуализации взрывов основаны на системе частиц и так или иначе используют её. И ещё очень долго система частиц так и будет оставаться главным способом визуализации взрывов.
Литература:
- Lin, Gong Visual Simulation of Explosion Effects Based on Mathematical Model and Particle System [Text] / Gong Lin, Hu Dingjun // Journal of Networks. — 2014. — vol. 9, no. 4. — p. 1020–1026
- Reeves, W. T. Particle Systems [Text] — A Technique for Modelling a Class of Fuzzy Objects / W. T. Reeves // ACM Transactions on Graphics. — 1983. — vol. 2, no. 2. — p. 91–108
- de Kruijf, Marc firestarter — A Real-Time Fire Simulator [Text] / Marc de Kruijf // Computer Science Capstone. — 2007.
- Monaghan, J. J Smoothed Particle Hydrodynamics [Text] / J. J. Monaghan // Annual Review of Astronomy and Astrophysics. — 1992. — no. 30. — p. 543–574
- Григорьев, А. Б. Методы и алгоритмы компьютерной графики для моделирования природных явлений и объектов в системах виртуальной реальности [Текст]: автореф. дис. на соиск. учён. степ. канд. тех. наук: 05.13.16: защищена 7.7.2000: утв. 17.7.2000 / Григорьев Андрей Борисович. — Санкт Петербург, 2000. — 16 с.

