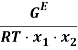Моделирование коэффициентов активности компонентов системы ацетон — пропанол с помощью уравнений Редлиха — Кистера, Маргулеса, Ван Лаара



В данной работе описываются способы определения коэффициентов активности изотермической системы ацетон — пропанол с помощью эмпирических методов расчёта.

1. Физико-химические свойства системы

Ацетон

Ацетон — Органическое вещество, имеющее формулу CH3–C(O)–CH3, простейший представитель насыщенных кетонов.

Температура плавления = -95°C;

Температура кипения = 56.1 °C;

Плотность = 0,7899 г/см³;

Молярная масса = 58,08 г/моль.

Основную часть ацетона получают как сопродукт при получении фенола из бензола по кумольному способу.

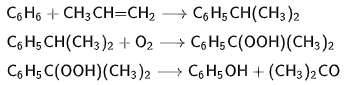
Пропанол

Пропанол — одноатомный спирт. Встречается в природе в небольших количествах как продукт ферментации. Бесцветная жидкость со спиртовым запахом, смешивается с водой и образует с ней азеотропную смесь. Растворим в этаноле, диэтиловом эфире, ацетоне, бензоле и других органических растворителях.

Температура плавления = -127 °C;

Температура кипения = 97,4 °C;

Плотность = 0,8 г/см³;

Молярная масса = 60,09 г/моль.

В промышленности 1–пропанол получают путём гидроформилирования этилена с последующим гидрированием образовавшегося пропаналя.

Исходные данные:

1) Бинарная система (ацетон — пропанол)

2) Паровая фаза считается идеальной (подчиняется закону Дальтона)

3) Давления насыщенных паров компонентов системы рассчитаны по уравнению Антуана

4) Коэффициенты активности компонентов системы рассчитаны по методу UNIFAC

5) Система изотермическая (25 ⁰С)

Подставив исходные данные в программу ChemSep, были получены данные о равновесии в системе:

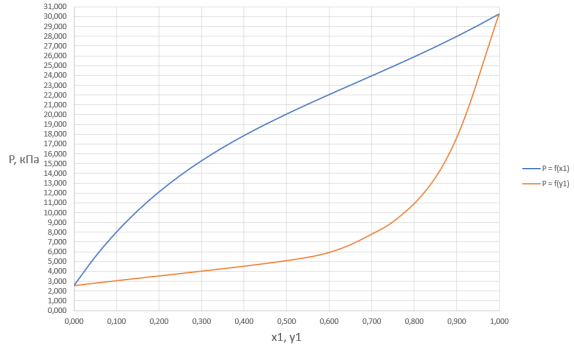
Рис. 1. График зависимости общего давления в системе от содержания ацетона в жидкой и газовой фазах

Таблица 1

Составы равновесных фаз для системы ацетон (1) –пропанол (2) при общем давлении Ри температуре 25º C

Температура, 0С	доля C3H6O в жидкой фазе	доля C3H6O в паровой фазе	Общее давление, кПа
25,000	0,000	0,000	2,573
25,000	0,050	0,556	5,510
25,000	0,100	0,710	8,036
25,000	0,150	0,782	10,224
25,000	0,200	0,825	12,134
25,000	0,250	0,853	13,816
25,000	0,300	0,874	15,312
25,000	0,350	0,890	16,659
25,000	0,400	0,902	17,885
25,000	0,450	0,913	19,018
25,000	0,500	0,922	20,080
25,000	0,550	0,931	21,089
25,000	0,600	0,938	22,064
25,000	0,650	0,946	23,021
25,000	0,700	0,953	23,973
25,000	0,750	0,960	24,934
25,000	0,800	0,967	25,916
25,000	0,850	0,975	26,931
25,000	0,900	0,982	27,992
25,000	0,950	0,991	29,110
25,000	1,000	1,000	30,297

Давление чистого C3H6O, кПа	Давление чистого C3H7OH, кПа
30,297	2,573

В связи с низким общим давлением в системе при заданной температуре и отсутствием сильной ассоциации компонентов в паровой фазе считаем данную паровую систему идеальной. При этом допущении расчет коэффициентов активности компонентов возможен по уравнению:

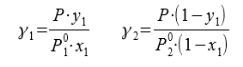
Где х₁, у₁ — доли ацетона в жидкой и паровой фазах соответственно

Р — общее давление в системе

,− давление чистых ацетона и пропанола соответственно

Построив график зависимости ln(γ₁/γ₂) = f(x₁), можем сделать вывод о термодинамической согласованности данных.

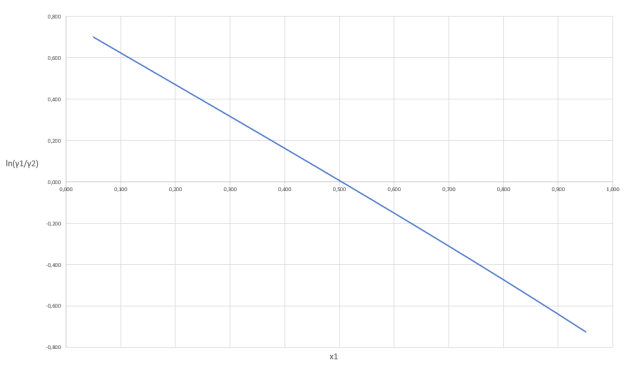
Рис. 2. График зависимости логарифма отношения коэффициентов активности от содержания ацетона в жидкой фазе

Так как площадь под графиком равна 0, то система является термодинамически согласованной.

2. Расчет системы согласно эмпирическим моделям

Эмпирические модели негодны для корреляции и предсказания данных, они служат лишь для математического описания массива данных о коэффициентах активности компонентов.

Модель Редлиха — Кистера

Одна из наиболее обширно применяемых эмпирических моделей была предложена Редлихом и Кистером в 1948 г. В ней применяются следующие уравнения для коэффициентов активности:

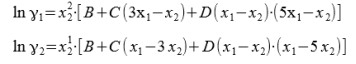
Для нахождения параметров B, Cи D по экспериментальным данным используется следующее уравнение:

При x₁ = x₂ = 0,5 первое и третье слагаемые уравнения обращаются в ноль и можно найти параметр С = 0.016:

При x₁ = 0,1464 третье слагаемое уравнения обращается в ноль и можно найти параметр В = 0.788:

При x₁ = 0,2113 второе слагаемое уравнения обращается в ноль и можно найти параметр D = 0.012:

Модель Маргулеса

Еще ранее была предложена эмпирическая модель Маргулеса, в которой lnɣ1 и lnɣ2 для бинарных систем рассчитываются с помощью линейных перегруппировок степенных рядов:

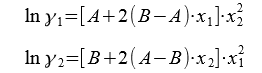
Для расчета параметров А и В используется линейная зависимость:

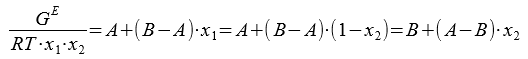
Значения избыточной энергии Гиббса для каждой точки состава находим по уравнению:

Таблица 2

Значение избыточной энергии Гиббса ифункции

Доля C3H6O вжидкой фазе
0,000	-0,061	-2,466
0,050	91,667	0,779
0,100	173,811	0,779
0,150	246,457	0,780
0,200	309,604	0,781
0,250	363,241	0,782
0,300	407,366	0,783
0,350	441,948	0,784
0,400	466,972	0,785
0,450	482,402	0,787
0,500	488,176	0,788
0,550	484,275	0,790
0,600	470,610	0,791
0,650	447,125	0,793
0,700	413,752	0,795
0,750	370,392	0,797
0,800	316,937	0,800
0,850	253,303	0,802
0,900	179,357	0,804
0,950	94,969	0,807
1,000	0,061	2,466

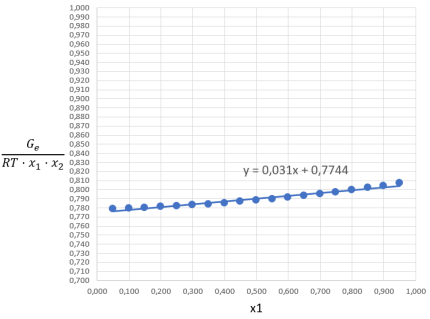
Рис. 3. График зависимости от содержания ацетона в жидкой фазе

Построив график зависимости функции = f(х₁) находим параметр

А = 0,7744 при х₁ = 0.

По значению тангенса угла наклона прямой рассчитываем параметр В:

В = tg(ɑ) + А = 0,031 + 0,7744 = 0,8054

Модель Ван Лаара

Для моделирования коэффициентов активности часто применяются такжe эмпирические уравнения Ван Лаара:

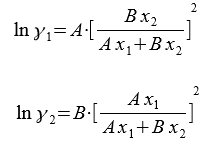
Для определения параметров А и В используется линейная зависимость:

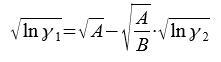
Таблица 3

Значение и

Доля C3H6O в жидкой фазе
0,000	–	0,000
0,050	0,839	0,044
0,100	0,795	0,088
0,150	0,752	0,131
0,200	0,709	0,175
0,250	0,665	0,219
0,300	0,622	0,263
0,350	0,579	0,307
0,400	0,535	0,351
0,450	0,492	0,395
0,500	0,448	0,440
0,550	0,404	0,484
0,600	0,361	0,529
0,650	0,317	0,574
0,700	0,272	0,619
0,750	0,228	0,665
0,800	0,183	0,711
0,850	0,138	0,758
0,900	0,092	0,805
0,950	0,839	0,000
1,000	0,795	0,044

Построив линейную зависимость, определяем константы уравнения Ван Лаара.

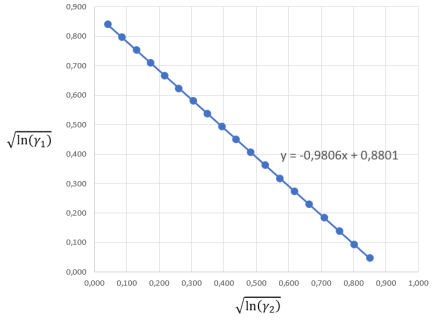
Рис. 4. График зависимости от

Отрезок, отсекаемый прямой на оси ординат, соответствует √A = 0,8801, откуда А = 0,775.

Тангенс угла наклона прямой, откуда В = 0,806.

Точность рассмотренных выше моделей обычно хорошо описывают системы малой или умеренной неидеальности и недостаточна для систем с большими отклонениями от идеального поведения.

Уравнение Редлиха — Кистера, Маргулеса, Ван Лаара и связанные с ними алгебраические выражения характеризуются относительной простотой математического аппарата, легкостью оценки параметров по данным о коэффициентах активности и адекватным описанием двухкомпонентных смесей, значительно отклоняющихся от идеальных, включая частично растворимые жидкие системы. Однако, эти уравнения не подходят к многокомпонентным системам, если отсутствуют параметры взаимодействия между тремя и более компонентами.

Литература:

1. Гайле А. А., Сомов В. Е., Процессы разделения и очистки продуктов переработки нейти и газа: Учеб.пособие. — Спб.: ХИМИЗДАТ, 2012. — 376 с.
2. Несмеянов А. Н., Несмеянов Н. А., Начала органической химии. т.1- М.: Химия, 1969. — 664 с.
3. Соколов В. 3., Харлампович Г. Д., Производство и использование ароматических углеводородов — М.:Химия, 1980. — 336 с.
4. Справочник химика. Том 1. Общие сведения, строение вещества, свойства важнейших веществ, лабораторная техника. / Под ред. Б. П. Никольского — М.-Л.: Химия, 1966–1071 с.