Пороговые криптосистемы как один из вариантов модификации асимметричных криптосистем

Ключевые слова: криптографическая система, асимметричная криптосистема, пороговые схемы разделения секрета, схема Шамира, пороговая криптосистема.

Криптографическая система — система, которая позволяет зашифровать открытый текст и затем расшифровать его. Используются такие системы для безопасной передачи данных по незащищённому каналу, то есть каналу, в котором данные могут быть перехвачены злоумышленником в процессе передачи. Если данные будут передаваться между абонентами в исходном виде, то злоумышленнику для получения необходимой информации будет достаточно просто перехватить эти данные в процессе передачи. Если же передача данных будет осуществляться в зашифрованном виде, то задача злоумышленника значительно осложниться, так как теперь перехваченные данные потребуется ещё и расшифровать. Поскольку, в современных криптосистемах используются сложные математические алгоритмы, то, не зная нужного ключа, расшифровать данные становится практически невозможно.

Одним из вариантов криптографических схем являются пороговые криптосистемы, которые представляют собой модификацию асимметричной криптосистемы.

Для начала рассмотрим обычную асимметричную криптографическую систему. В такой системе каждая из сторон имеет два ключа:

– открытый ключ, при помощи которого передаваемая информация шифруется отправителем;

– секретный ключ, который используется получателем для расшифровки полученного шифротекста.

На рисунке 1 продемонстрирована схема работы ассиметричной криптосистемы.

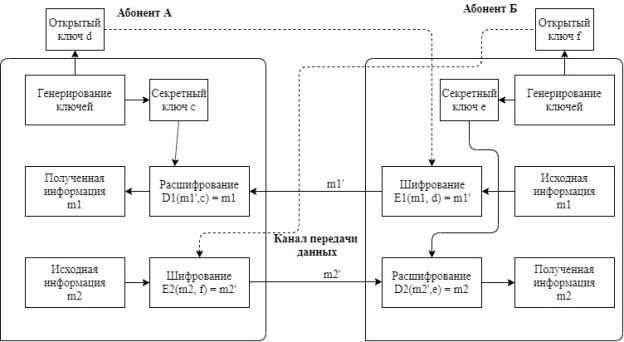
Рис. 1.

Предположим, что абонент А хочет передать информацию абоненту Б. Для этого он с помощью функции E2 шифрует данные, входными параметрами этой функции являются передаваемая информация m2 и открытый ключ абонента Б — f. На выходе функции E2 получаем шифротекст m2’, который передаётся абоненту Б. Расшифровка полученной информации осуществляется при помощи функции D2, входными параметрами которой являются полученный шифрованный текст m2’ и секретный ключ абонента Б — e. На выходе функции D2 получаем исходную передаваемую информацию m2. Аналогично происходит передача информации от абонента Б абоненту А.

Пороговые криптосистема отличаются от рассмотренного выше примера тем, что значение секретного ключа разделено между определённым количеством участников (n) при помощи пороговой схемы разделения секрета. Для того, чтобы получить значение секретного ключа, а значит и расшифровать полученные данные требуется знать k из n частей секретного ключа (k

Итак, пусть значение секретного ключа S=53, число участников между которыми будем делить это значение n=4, а число частей, которое потребуется для восстановления ключа k=3. В данном примере будем использовать пороговую схему разделения секрета Шамира, которая основана на полиномиальной интерполяции.

Разделение секрета.

В общем случае полином будет иметь вид f(x)=a₀+a₁x+a₂x²+…+a_k-1x^k-1 mod(p), где:

– a₀ =S;

– a₁,a₂,…,a_k-1 — положительные целые числа, которые выбираются случайным образом.

– p — простое число, которое является порядком конечного поля, то есть поля, элементами которого являются целые числа 0, 1, 2,…, p-1, а все математические операции в этом поле производятся по модулю p. Пусть в нашем случае p=79.

Поскольку в нашем случае k=3, то пусть полиномиальная функция будет следующая f(x) = 53+2x+5x² mod(79). Случайным образом получим следующие фрагменты секретного ключа: (4, 62), (9, 2), (12, 7) и (18, 50). На этом разделение секрета заканчивается.

Восстановление секрета

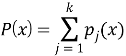
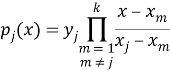
Поскольку значение секрета находится при x=0, воспользуемся немного изменёнными формулами:

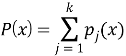
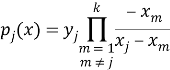
Тогда получим:

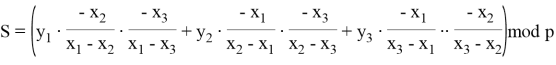
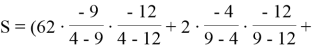
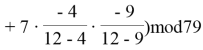
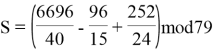
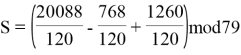
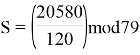
После решения полученного выражения получаем, что S=53. Таким образом, значение секретного ключа восстанавливается.

Ниже, на рисунке 2, продемонстрирована схема пороговой криптосистемы для случая, когда требуется 3 фрагмента для восстановления секретного значения.

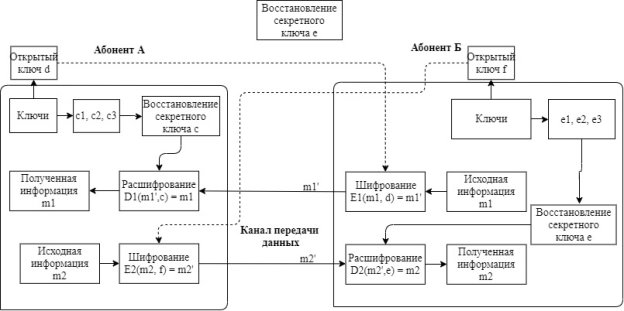
Рис. 2.

В этом случае секретные ключи абонентов заменились на их доли. У абонента А — c1, c2, c3, у абонента Б — e1, e2, e3. Затем с помощью этих долей восстанавливается значение секретного ключа, и только потом полученные данные расшифровываются. Стоит заметить, что число известных долей должно быть не менее k, в противном случае значение секретного ключа не восстановится.

Литература:

1. Описание симметричного и асимметричного шифрования // Microsoft. URL: https://support.microsoft.com/ru-ru/help/246071. (дата обращения: 20.11.2019).
2. Зыбкин А. Ю. Исследование эффективности применения схемы разделения секрета Шамира в области информационной безопасности: диплом. работа. Санкт-Петербургский государственный морской технический университет, СПб, 2019.
3. Adi Shamir. How to Share a Secret/ Adi Shamir// Massachusetts Institute of Technology. — 1979. — Ноябрь. — c. 612–613