Криптосистема RSA — ассиметричная система с открытым ключом, названная в честь ее создателей: Rivest, Shamir, Adleman. Несмотря на то, что после создания криптосистемы прошло уже около сорока лет, она до сих пор остается самой используемой из всех систем со схожими алгоритмами работы из-за вычислительной сложности задачи факторизации больших целых чисел. Примечателен тот факт, что RSA стала первой системой, пригодной как для шифрования, так и для цифровой подписи.
Идея RSA заключается в том, что пользователь создает и публикует открытый ключ, основанный на двух больших простых числах вместе со вспомогательным значением, причем сами числа должны храниться в тайне. Благодаря этому, любой человек может воспользоваться открытым ключом для шифрования своей информации, но если ключ будет достаточно большой, то для дешифрования потребуется наличие тех простых чисел, которые участвовали в создании данного ключа. Раскрытие RSA шифрования — одна из основных проблем на сегодняшний день, поскольку до сих пор нельзя говорить о том, что этот механизм абсолютно надежен.
Так что же послужило толчком для создания такой криптосистемы как RSA? Дело в том, что после опубликования статьи Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии», о которой ранее уже упоминалось, трое ученых Рональд Ривест, Ади Шамир (специалисты в сфере компьютерных технологий) и Леонард Адлеман (математик) из Массачусетского технологического института (MIT) приступили к поискам математической функции, позволяющей в полной мере реализовать модель криптосистемы с открытым ключом. После рассмотрения многих вариантов, ученые все же нашли алгоритм, с помощью которого можно легко находить большие простые числа, но очень сложно раскладывать произведение двух простых чисел на множители.
Не так давно выяснилось, что еще до публикации описания алгоритма RSA, похожая по принципам работы схема шифрования была предложена одним британским криптографом из GCHQ. Однако, его разработка была засекречена и потому не была реализована в повседневной жизни.
Таким образом, криптографическая система RSA остается на сегодняшний день одной из самых надежных (при длине ключе от 1024 бит).
Алгоритм работы RSA содержит в себе четыре основных этапа: генерация ключей, их распределение, шифрование и дешифрование.
На этапе создания ключей производятся следующие операции:
- Выбираются два больших простых числа p и q.
-
Вычисляется их произведение
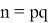 , называемое модулем.
, называемое модулем.
-
Вычисляется значение функции Эйлера от полученного произведения
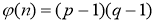 .
.
-
Выбирается произвольное число e, такое, что
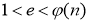 , причем
, причем 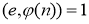
-
С помощью алгоритма Евклида вычисляется некоторое число d, удовлетворяющее условию
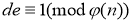 .
.
На этапе распределения ключей:
- Пара {e,n} выступает в качестве открытого ключа RSA.
- Пара {d,n} выступает в качестве закрытого ключа RSA.
На этапе шифрования и дешифрования:
Со стороны отправителя:
- Взять открытый ключ {e,n} получателя.
- Взять открытый текст m.
-
Зашифровать сообщение с использованием открытого ключа получателя:
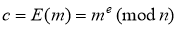 .
.
Со стороны получателя:
- Принять зашифрованное сообщение C.
- Взять свой закрытый ключ (d,n).
-
Применить закрытый ключ для дешифрования сообщения:
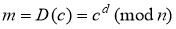 .
.
Рассмотрим пример создания ключей шифрования и дешифрования в криптографической системе, строго следуя алгоритму, обозначенному в предыдущем пункте. Для упрощения вычислений, будем выбирать небольшие простые числа.
Пример. Этап создания ключей:
1.Выберем два простых числа![]() и
и ![]() , причем таких, что
, причем таких, что ![]() . Пусть
. Пусть ![]() и
и ![]() ;
;
2.Вычислим произведение взятых чисел: ![]()
3.Вычислим функцию Эйлера. Для этого воспользуемся формулой ![]() . Тогда
. Тогда ![]() ;
;
4.Выберем произвольное число e. Пусть ![]() ;
;
5.С помощью алгоритма Евклида вычислим число d, удовлетворяющее условию ![]() . Получим
. Получим ![]() .
.
Переходим к этапу распределения ключей.
- Назначаем пару {3,9173503} в качестве открытого ключа;
- Назначаем пару {6111579,9173503} в качестве закрытого ключа.
Теперь, когда в наличии имеются открытый и закрытый ключи, можно приступать к этапу шифрования.
-
Выбираем некоторый текст m, который необходимо зашифровать (шифрование будем выполнять с помощью открытого ключа). Пусть
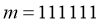 .
.
-
Шифруем сообщение с использованием открытого ключа получателя:
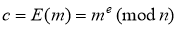 .
.
![]() .
.
Заключительным этапом будет этап дешифрования.
-
Возьмем полученный зашифрованный текст c и дешифруем его с помощью закрытого ключа
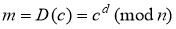 .
.
Итак, поскольку ![]() , то
, то
![]() .
.
Из рассмотренного выше примера видно, что криптографическая система RSA действительно работает, причем именно по тому алгоритму, что использовался для решения примера. Отличие лишь в том, что при реальных условиях использования системы выбираются достаточно большие простые числа.
Литература:
- RSA [электронный ресурс] — Режим доступа: URL: https://ru.wikipedia.org/wiki/RSA. Дата обращения 06.10.2019.
- Бернет С., Пэйн С. Криптография. Официальное руководство RSA Security/ Бернет С., Пэйн С. — Бином, 2002–381с.
- Виноградов, И. М. Основы теории чисел: учебное пособие [Текст] / И. М. Виноградов. — 12-е изд. — М.: Лань, 2009. — 176 с.
- Коутинхо С. Введение в теорию чисел. Алгоритм RSA/ Коутинхо С. — М.: Постмаркет, 2011 -328с.

