Современный компьютерный томограф представляет собой сложный программно-технический комплекс. Механические узлы и детали выполнены с высочайшей точностью. Для регистрации прошедшего через среду рентгеновского излучения используются сверхчувствительные детекторы. Система достаточно дорогая в производстве, однако можно уменьшить её стоимость посредством уменьшения количества детекторов на матрице. Конечно, качество изображения и информативность получаемых рентгеновских снимков изменится, но возможно найти компромисс между качеством получаемого изображения и стоимостью всей установки путем оптимизации параметров системы.
Данная работа посвящена возможности использовать в медицинских целях широко-конусных пучков рентгеновских излучений со смещенной матрицей, и калибровки КТС (компьютерной томографической системы).
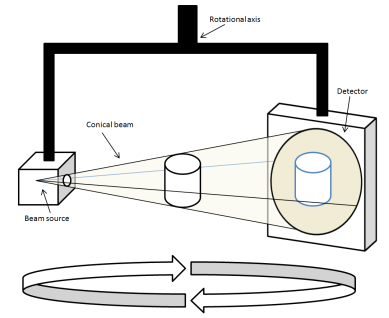
Рис. 1. Принцип работы КЛКТ
Постановка задачи. При конусно-лучевой компьютерной томографии объемное изображение получается путем реконструкции из набора плоских проекций, которые отражают результаты просвечивания объекта рентгеновским пучком с разных сторон (Рис. 1). Процесс получения плоских проекций заключается в следующем. Рама, к которой прикреплены источник рентгеновского излучения и матрица детекторов с противоположной стороны, вращается вокруг пациента, находящегося на диагностическом столе. Затем происходит серия экспозиций с N заданных углов и фиксация полученных проективных изображений.
Полученные проекции исходных данных обрабатываются для создания объемного набора данных и могут быть объединены в одном объекте для визуализации.
В качестве детекторов обычно используется плоско-панельный детектор, состоящий из сцинтиллятора йодида цезия с массивом тонкопленочных транзисторов из аморфного кремния. Йодид цезия преобразует рентгеновские частицы в световые фотоны, а тонкопленочный транзистор вырабатывает электроны пропорционально интенсивности падающего фотона. Этот электрический заряд сохраняется в матрице, затем считывается и преобразуется в цифровые данные, передаваемые на процессор обработки изображения.
Решим последовательно следующие задачи:
1) Опишем математические модели деформирования матрицы детекторов.
2) Опишем процедуру калибровки КТС.
3) Опишем алгоритм, с помощью которого дополним полученные изображения с урезанной матрицей до полноразмерных.
Математические модели деформирования матрицы детекторов
Предположим, что максимальное отклонение точек матрицы от номинальных значений может достигать 0,5 см. Полагая также деформацию матрицы гладкой до второго порядка включительно, будем описывать калибровочные функции сплайнами второго порядка (по пространственным переменным) со стыковкой второго порядка на границах сетки. Учитывая параметры наблюдаемых деформаций можно считать, что производные второго порядка по пространственным переменным не превосходят значения:
= 2 * k1 = 2 * 0.5см / (3,55см)2 ≈ 0,0793см-1.
Данная величина получена из математической модели деформации:
d(x) = k1 * x2 + k2, при этом k2 = -0,5см и k1 * (3,55см)2 + k2 = 0.
Таким образом, чтобы восстановить калибровочные функции, обеспечивающие точность коррекции отдельной проекции изображения до 1ps, необходимо и достаточно (в рамках описанной модели) определить координаты реперных точек с размером ячейки на детекторной матрицы
Δ = 0,7 см. Данная величина получена из равенства 0,5 * * (0,5 * Δ)2 = 0,5ps.
Процедура калибровки
При сканировании фантома калибровки, мы получаем координаты, для каждого из 24 шариковых подшипников, в двумерном пространстве матрицы детекторов:
№ 1 шарик → (i1, j1) № 1 шарик → (,)
№ 2 шарик → (i2, j2) № 2 шарик → (,)
… …
№ 24 шарик → (i24, j24) № 24 шарик → (,)
Где i и j координаты пикселей в матрице. Сравнивая полученные координаты ШП с номинальными координатами (Рис. 2), можем найти разницу в расположении ШП и построить отображения калибровочных функций со сдвигом детекторов:
Rφ(i, j) = Rφ (,), где i = 0: 256 и j = 0: 512
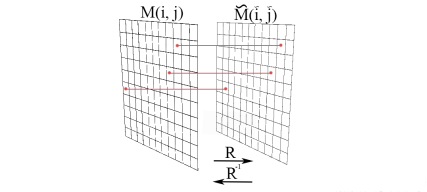
Рис. 2. Сравнение полученных координат ШП с номинальными
КТС со смещенной матрицей
Так как производство КЛКТ достаточно дорогое, мы можем сэкономить на создании матрицы детекторов. Мы уменьшаем физический размер матрицы до 200px х 512px как показано на Рис. 3 (участок № 1) и она оказывается смещенной относительно рамы, к которой прикреплена. При сканировании объекта, полученные изображения будут неполными из-за недостающего куска матрицы. Мы опишем алгоритм, с помощья которого дополним полученные изображения с урезанной матрицей до полноразмерных.
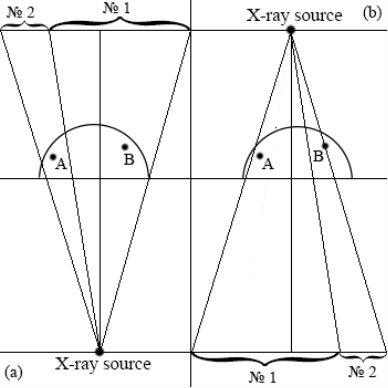
Рис. 3. Дополнение урезанной матрицы
Для каждого угла поворота мы получаем изображение с откалиброванной матрицей детекторов, размером 200px x 512px. Как видно из Рис. 3(а) у нас нет данных сканирования для точки А. Чтобы их получить, нам необходимо восстановить участок № 2 размером 56px x 512px. Так как у нас есть данные сканирования для каждого угла (ϕ = 0о: 360о), мы берем кусок участка № 1 изображения, повернутого на угол 180о (Рис. 4(b)) относительно исходного изображения, где i = 0: 56px и j = 0: 512px (i и j — расположение детекторов на матрице) и восстанавливаем кусок № 2 (Рис. 3(a)). Проделываем аналогичную работу для каждого изображения, полученных при угле (ϕ = 0о: 360о).
Таким образом мы получаем восстановленные данные для каждого угла и получаем полноразмерные изображения без потери качества и информативности. Конечно, восстановленные данные будут отличаться от данных, полученных при полной матрице, но мы нашли компромисс между размерами матрицы и качеством полученных изображений.
Литература:
- A. Jaffray, J. H. Siewerdsen, J. W. Wong, and A. A. Martinez, “Flatpanel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 1337–1349 s2002d.
- Cho Y, Moseley DJ, Siewerdsen JH, Jaffray DA, “Accurate technique for complete geometric calibration of cone-beam computed tomography systems”.

