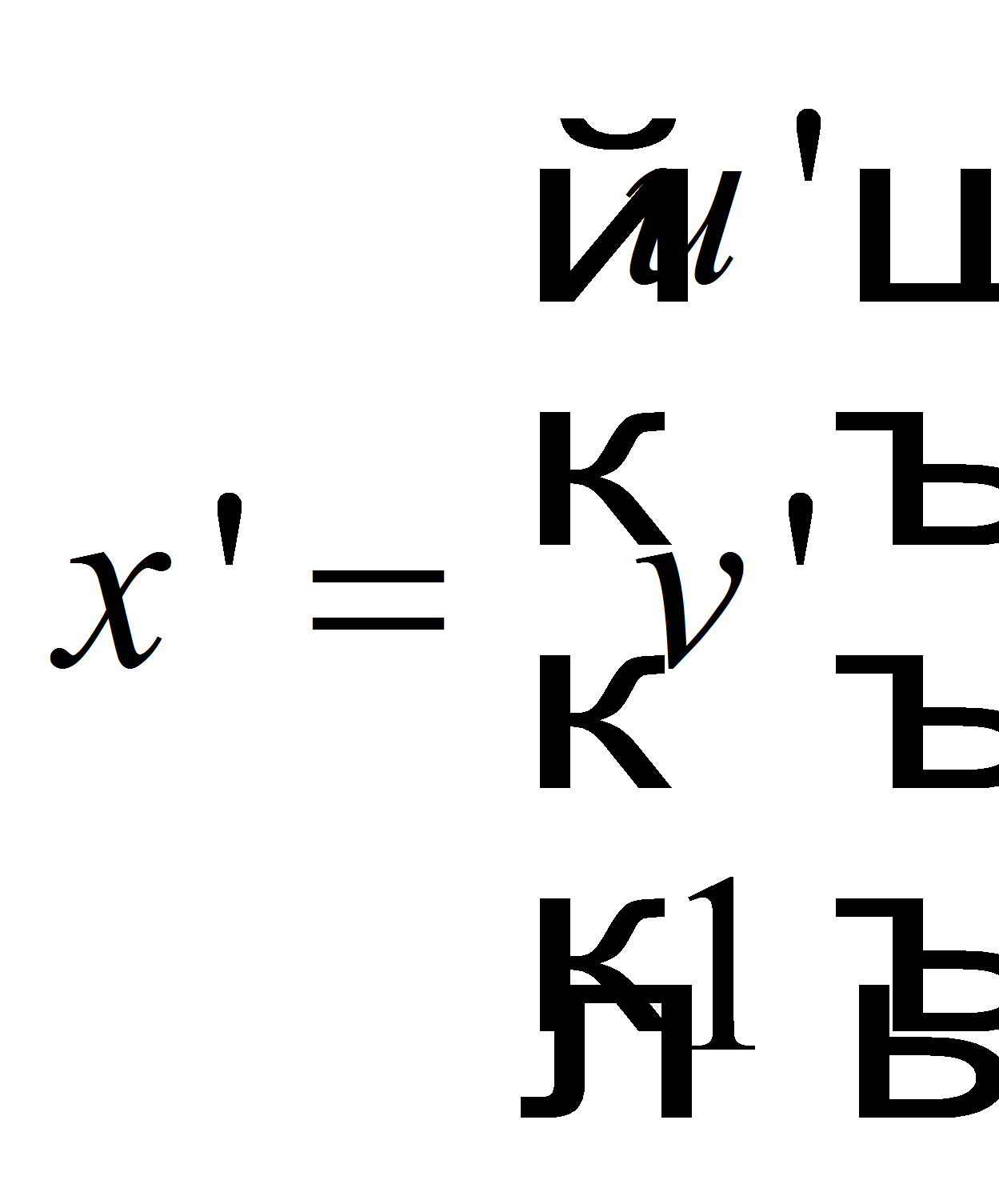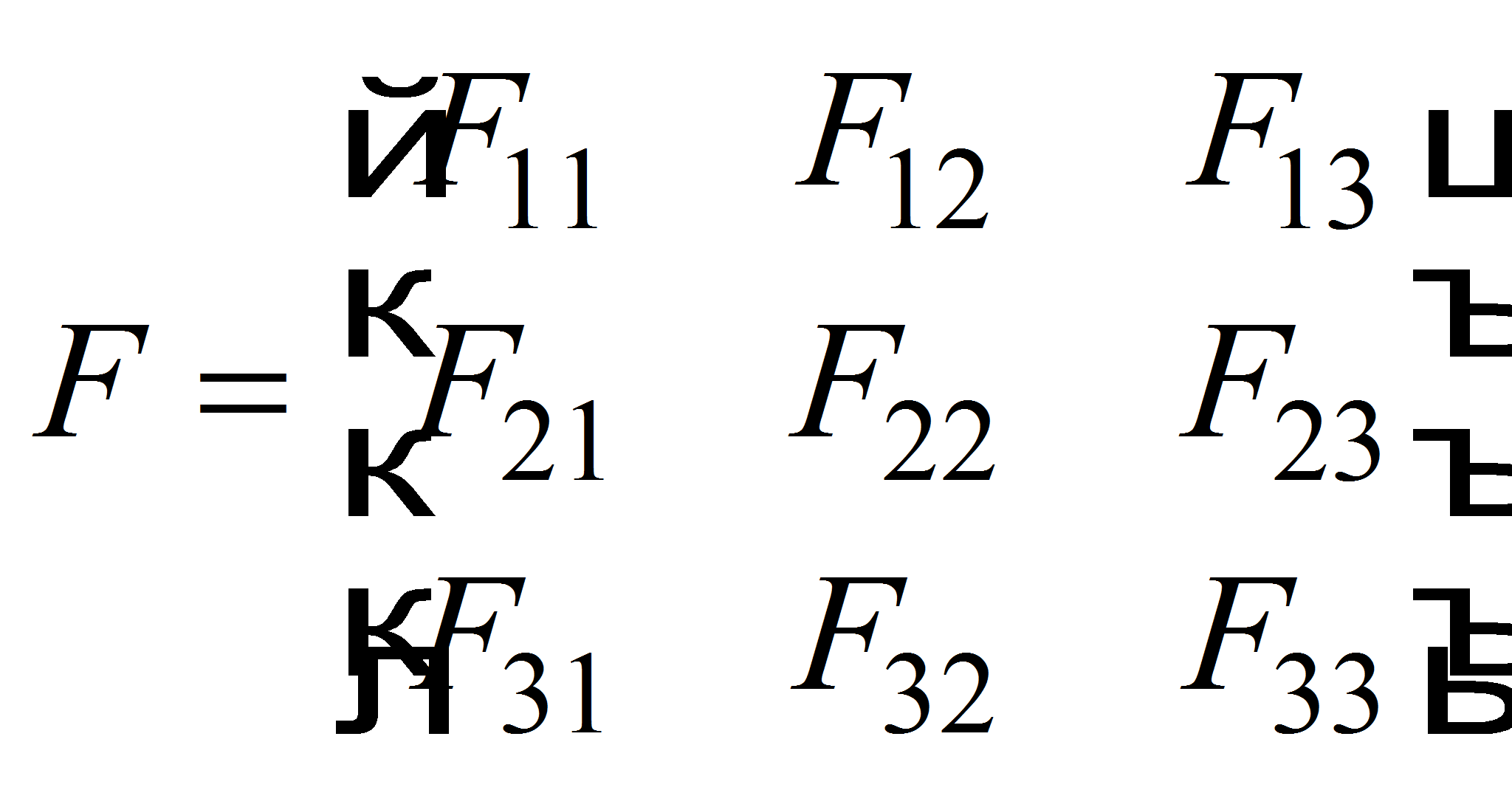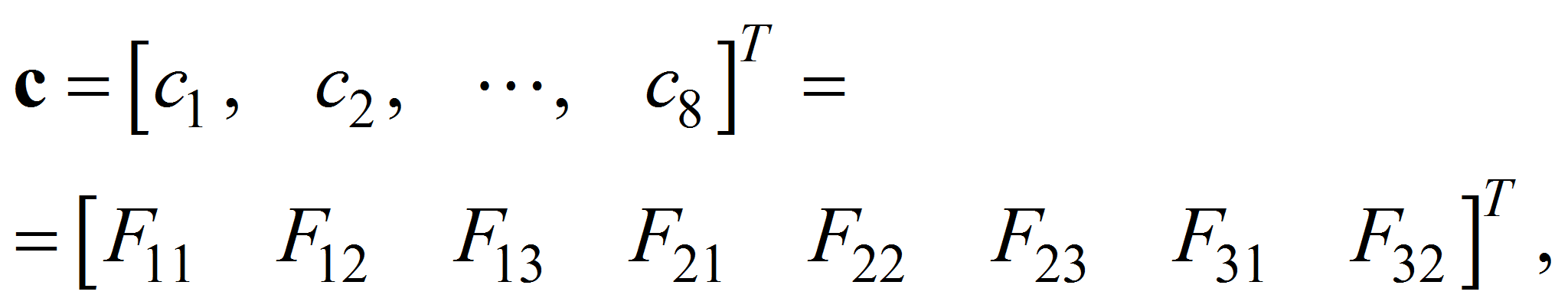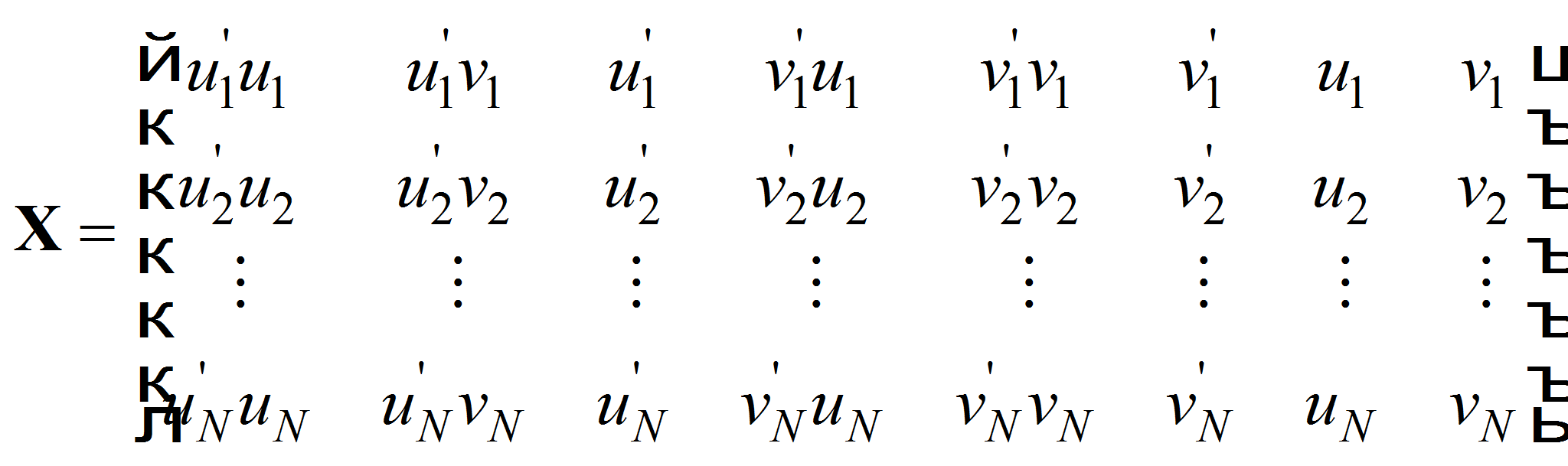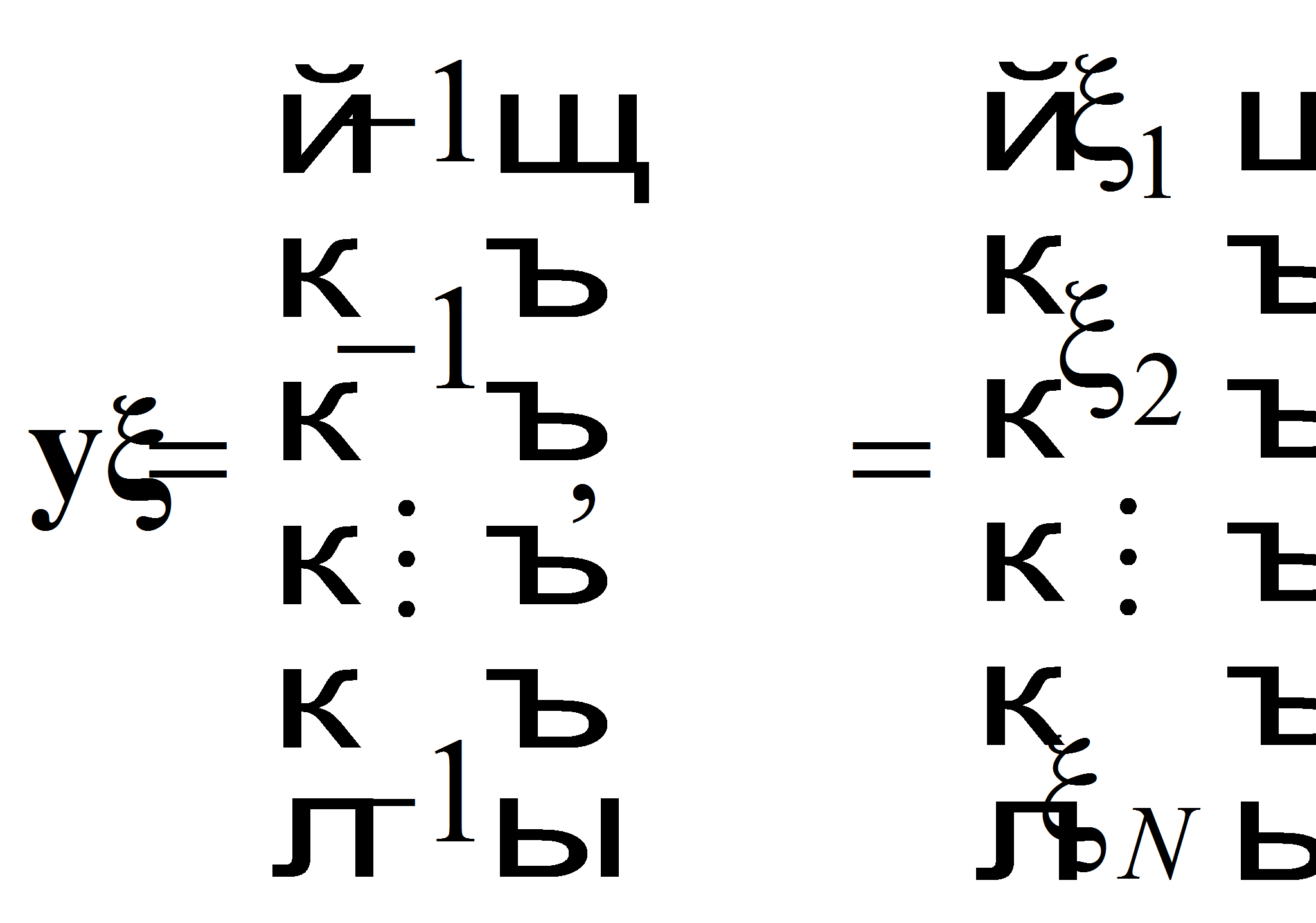Метод согласованной идентификации в задаче ректификации изображений

В работе рассматривается задача ректификации изображений, заключающаяся в формировании строк соответственных точек на изображениях с использованием фундаментальной матрицы, формируемой по небольшому числу заданных соответственных точек. Для нахождения фундаментальной матрицы предлагается новый подход, основанный на согласованной идентификации.

Введение

Задача ректификации изображений, заключающаяся в формировании строк соответственных точек на изображениях, является одной из распространенных и востребованных задач обработки изображений. Эта проблема является актуальной в задачах построения цифровой модели рельефа (ЦМР), нахождения ключевых точек для формирования HOG-дескрипторов в задаче распознавания и др.

Для построения преобразований используется так называемая фундаментальная матрица [1][2], формируемая по небольшому числу заданных соответственных точек. Для нахождения фундаментальной матрицы обычно используется алгоритм RANSAC [3],[4]. При использовании этого алгоритма ищется единственный набор данных, наилучшим образом соответствующих модели в заданном смысле.

Популярность этого алгоритма связана с его высокой устойчивостью к грубым ошибкам типа сбоев. На сегодняшний день он признается одним из наиболее эффективных в условиях сильного зашумления исходных данных. Тем не менее, построение модели лишь на одном наборе данных, иногда приводит к грубым ошибкам в определении модели.

В настоящей работе предлагается новый подход к определению параметров моделей в условиях сильной зашумленности, основанный на согласованной идентификации [5]. Идея метода состоит в определении модели по некоторому подмножеству наиболее согласованных данных. В работе рассматривается применение этого метода к задаче определения фундаментальной матрицы.

1. Формулировка задачи построения фундаментальной матрицы

Рассмотрим общую задачу восстановления сцены по двум видам. Эта задача решается в рамках эпиполярной геометрии – проективной геометрии между двумя изображениями.

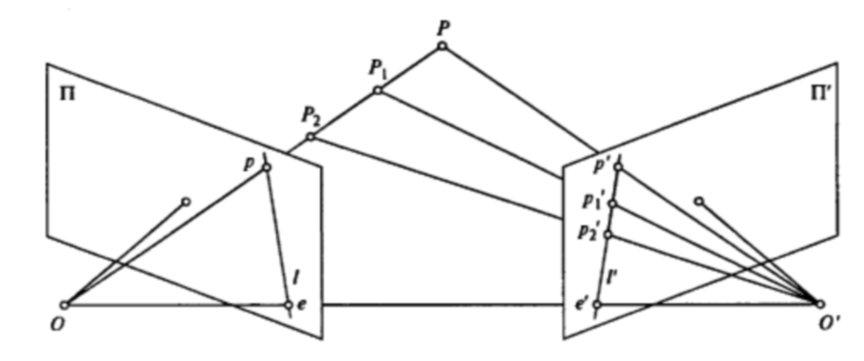
Пусть имеются две камеры с центрами проекций в точках O и O’, плоскости проекций П и П' этих камер, и некоторая точка P в пространстве (рис. 1).

Рис. 1. Модель эпиполярной геометрии

Точки e и e’, пересечения линии OO’ с плоскостями П и П’, называются эпиполюсами, а линии l и l’, пересечения плоскости OO’P с плоскостями П и П’, – эпиполярными линиями для точки P. Точки на двух изображениях, которые являются проекциями одной и той же точки сцены, называются соответственными.

Соответственные точки на двух проекциях связаны фундаментальной -матрицей , в частности, для соответственных точек, координаты которых заданы 3×1-векторами ,:

выполняется условие

, (1)

где .

Для одной пары заданных соответственных точек соотношение (1) является линейным однородным уравнением относительно коэффициентов фундаментальной матрицы.

Для N пар () соответственных точек, полагая во всех соотношениях , можно записать систему N неоднородных линейных уравнений [6] вида

, (2)

где с – вектор искомых параметров, составленный из коэффициентов фундаментальной матрицы F:

а -матрица X и -векторы y и определяются как

,

.

Здесь – ошибки, связанные с неточным заданием координат соответственных точек.

Оценку вектора с, составленного из элементов фундаментальной матрицы, можно получить применяя метод наименьших квадратов (МНК). Поскольку МНК чувствителен к грубым ошибкам, которые могут иметь место при задании соответственных точек, обычно применяют алгоритм RANSAC.

Как уже отмечалось выше, алгоритм RANSAC обладая несомненно высокой точностью, в ряде случаев оказывается недостаточно надежным, т.к. для построения модели используется единственный набор данных. В настоящей работе исследуется возможность повышения надежности оценок за счет применения метода согласованной идентификации, как альтернативы RANSAC.

2. Описание алгоритма

В методе согласованной идентификации из исходной системы (2) формируется множество так называемых подсистем нижнего уровня:

, k=1,2,…, (3)

где

, , ,

G – диагональная матрица, составленная из нулей и единиц: (рассматривается простейший случай согласованной идентификации, когда подсистемы нижнего уровня задаются квадратными матрицами ). Ясно, что при этом число подсистем нижнего уровня не превышает .

Вычисляя для каждой из построенных таким образом подсистем МНК-оценку:

(4)

получаем множество всех возможных оценок на подсистемах нижнего уровня:

Аналогичным образом (из нулей и единиц) строится множество диагональных P×P- матриц H_l:

.

С использованием этих матриц формируются так называемые подсистемы верхнего уровня:

, (5)

где

, , , .

Каждой подсистеме верхнего уровня принадлежит некоторое множество подсистем нижнего уровня и, соответственно, множество оценок (4):

, .

Для характеристики множеств вводится критерий взаимной близости оценок:

,

где .

Множество , для которого принимает минимальное значение, называют наиболее согласованным. Задача заключается в отыскании этого множества и построении на нем точечной оценки. По существу задача сводится к отысканию индекса :

.

3. Результаты экспериментальных исследований

Экспериментальные исследования метода согласованной идентификации проводились с целью проверки применимости этого метода к поставленной задаче.

На рисунках 2 и 3 приведен примеры нахождения соответственных точек и ректификации стереоизображений. Показанные на рисунках эпиполярные линии определены с использованием фундаментальной матрицы, которая оценивалась методом согласованной идентификации. Несовпадение соответственных точек с эпиполярными прямыми связано с особенностями нахождения фундаментальной матрицы.

Рис. 2. Эпиполярные прямые

Рис. 3. Ректифицированные изображения

В дальнейшем, соответственные точки находятся на эпиполярных линях любым известным методом, например, с использованием нормированного коэффициента корреляции. Применение метода согласованной идентификации позволяет добиться высокой точности и надежности определения коэффициентов фундаментальной матрицы, что в конечном итоге обеспечивает высокую точность обнаружения соответственных точек.

Заключение

Показана возможность достижения высокой точности формирования фундаментальной матрицы и определения соответственных точек с использованием метода согласованной идентификации. К сожалению, вычислительная сложность метода согласованной идентификации выше, чем у алгоритма RANSAC, однако это не является серьезным препятствием для применения метода, т.к. достижение максимальной точности обычно является важнейшим требованием. Кроме того, при реализации на многопроцессорных системах это не является серьезной проблемой, т.к. алгоритм обладает высокой степенью параллелизма.

Литература:

1. Mallon, J. Projective Rectification from the Fundamental Matrix / John Mallon, Paul F. Whelan // Image and Vision Computing. – 2005. – Vol. 21. – P. 643-650.

2. Hartley R.I. Theory and Practice of Projective Rectification / Richard I. Hartley // International Journal of Computer Vision. – 1999. – Vol. 35. – P. 115-127.

3. Fischler M.A. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography / Martin A. Fischler, Robert C. Bolles // Communications of the ACM. – 1981. – Vol. 24. – P. 381-392.

4. Torr P.H.S. The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix / P.H.S. Torr, D.W. Murray // International Journal of Computer Vision. – 1997. – Vol. 24. – P. 271-300.

5. Фурсов В.А. Согласованная идентификация управляемого объекта по малому числу наблюдений / В.А. Фурсов // Мехатроника, автоматизация, управление. – 2010. – № 3(108). – С. 2-8. – ISSN 1684-6427.

6. Форсайт Д. Компьютерное зрение. Современный подход / Форсайт Д., Понс Ж. – М.: Издательский дом "Вильямс", 2004. - 928 с.