Тема урока: «Геометрические фигуры. Что изучает геометрия?»
УМК «Планета Знаний» учебник М. И. Башмаков, М. Г. Нефёдова Математика 4 класс (1 часть)
Цели урока:
Обучающие: учить различать геометрические фигуры, чертить их, решать геометрические задачи, создать условия для формирования знаний о геометрии.
Развивающие: развивать у учащихся умения сравнивать, анализировать, делать выводы.
Воспитывающие: воспитывать у учащихся самостоятельность, повышение любови к математике.
Планируемые результаты:
Личностные: развивать внутреннюю позицию, познавательный интерес учебному материалу, к математике в целом.
Метапредметные: принимать и сохранять учебную задачу; планировать своё действие; осуществлять контроль по результату;определять и формулировать цель на уроке с помощью учителя; уметь высказывать своё мнение и уметь отстоять его; планировать свои действия в соответствии с поставленной задачей; уметь передавать свои мысли в устной форме; слушать и понимать речь других, договариваться; учиться работать в парах.
Предметные: различать геометрические фигуры, чертить их, решать геометрические задачи, создать условия для формирования знаний о геометрии
Оборудование: компьютер, проектор, индивидуальные карточки.
Ход урока:
I. Организационный момент. (2 минуты)
— Здравствуйте дети. Я рада видеть всех вас. Желаю, чтобы урок принес вам только положительные эмоции. Давайте улыбнемся друг другу, настроимся на рабочий лад и приступим к работе.
—Записываем число и классная работа и оставляем строчку для темы сегодняшнего урока.
II. Актуализация знаний. (10 минут)
На прошлом уроке у нас была контрольная работа, с которой удалось всем справиться. Сейчас я раздам ваши тетради, вы посмотрите свои отметки, и проведем небольшую работу над ошибками. Анализируя результаты контрольной работы, я определила, что большинство ошибок было допущено в ходе решения арифметических задач. Давайте попробуем вместе решить задачу из контрольной работы. (К доске вызываются дети, которые не справились с решением данных заданий в контрольной работе)
Задача. Маша и Миша покупали по карандашу. Маше не хватило 7 рублей, а Мише не хватило 11 рублей. Тогда они сложили свои деньги, купили один карандаш, и у них осталось 4 рубля. Сколько стоил карандаш?
Решение этой задачи начинается с анализа условия и выдвижения предположения, например, «Пусть карандаш стоил 20 рублей, тогда у Маши было 13 рублей, а у Миши 9 рублей.
1) 13 + 9 = 22 (руб.) — общее количество денег у детей.
2) 22–20 = 2 (руб.) — осталось у детей.
— Могло ли у детей остаться 4 руб., если бы они купили карандаш за 20 руб.?
Удобнее всего записать решение в виде таблицы:
|
Пусть карандаш стоил |
20 |
21 |
22 |
23 |
|
Тогда у Маши было бы |
13 |
14 |
15 |
16 |
|
А у Миши было бы |
9 |
10 |
11 |
12 |
|
Вместе у них было бы |
22 |
24 |
26 |
28 |
|
Сколько денег у них осталось бы после покупки одного карандаша на двоих? |
2 |
3 |
4 |
5 |
|
Мог ли карандаш столько стоить? |
нет |
нет |
да |
нет |
— Остались ли у вас еще вопросы по задачам из контрольной работы?
III. Открытие нового знания. (5 минут)
— Сегодняшняя тема урока зашифрована. Кто попытается отгадать ребусы?
(На доску выводятся слайды с названием геометрических фигур).
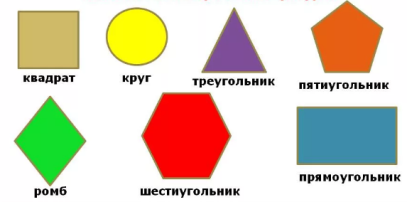
— Как называются все эти предметы?
— А какая наука изучает геометрические фигуры?
— Вернемся к пропущенной строчке и запишем тему урока.
— Открываем учебник на странице 106. Упражнение 1.
— Поднимаем руку и называем те фигуры, которые мы знаем?
— Кто найдет на фотографиях зданий, представленные на странице учебника, геометрические фигуры, которые только что называли?
— Геометрические фигуры могут быть пространственные и плоские. Те, которые изображены в упражнение 1, называются пространственные, т.к. они занимают место в пространстве и их можно рассмотреть с разных сторон. Их изображают всегда из хорошо знакомых нам плоских фигур.
— Давайте вспомним их, выполнив упражнение 2.
— Какие плоские фигуры использовали при изображении пространственных фигур из 1 упражнения.
— Кто может сказать, какие же важные задачи может решать такая наука, как геометрия?
— Прочитайте на странице 107.
IV. Решение частных задач (10 минут)
А теперь я предлагаю Вам выполнить следующее задание. Объединитесь в пары. Каждая пара получает лист с заданиями.
Задание 1. Жители города Геометрикус запутались. Они просят вас:
− назвать геометрические фигуры, изображенные на листе;
− разделить данные фигуры на группы;
− найти среди различных фигур треугольники, квадраты и прямоугольники.
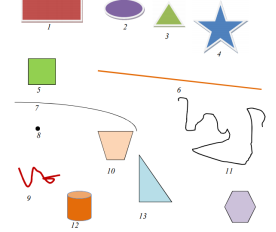
Задание 2. Жители города Геометрикус просят вас рассмотреть внимательно рисунки. Дорисовать в пустых клеточках фигуры таким образом, чтобы в каждой строке и каждом столбике было по пять разных предметов.
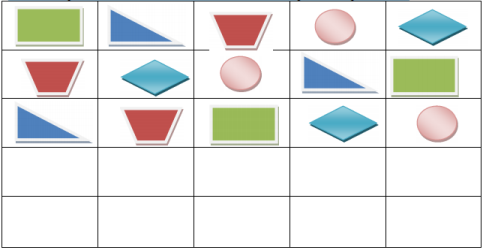
Задание 3. Жители города Геометрикус просят вас посмотреть на рисунок и вставить пропущенную фигуру. Продолжить данную последовательность и дорисовать фигуру

ФИЗ.МИНУТКА (2 минуты)
Много ль надо нам, ребята, Для умелых наших рук? Нарисуем два квадрата, А на них огромный круг, А потом еще кружочек, Треугольный колпачок. Вот и вышел очень, очень Развеселый чудачек. (Дети рисуют в воздухе геометрические фигуры.)
V. Закрепление знаний и способов действий. (10 минут)
— Продолжаем работу.
— Выполняем упражнение 6 на странице 107 (самостоятельно)
— А теперь давайте решим задачи. Упражнение 7(а, в).
— Для этого нам необходимо вспомнить, что же такое периметр, площадь квадрата и по каким формулам мы сможем их найти.
Площадь квадрата равна квадрату его стороны.
Периметр квадрата равен сумме его четырех сторон.
Формула для вычисления площади квадрата имеет следующий вид:
![]()
где a — сторона квадрата.
Формула для вычисления периметра квадрата следующая:
![]()
где a — сторона квадрата.
VI. Задавание домашнего задания (1 минута)
— Открываем дневники и записываем домашнее задание.
Страница 107 № 5(1 столбик), № 7(в)
VI. Итог урока. Рефлексия деятельности. (5 минут)
— Какая тема сегодня была на уроке?
— Что нового узнали?
— Сложно ли было?
— А теперь давайте подытожим наш урок.
Вместе с соседом по парте давайте составим синквейн. Вы уже знакомы с этой формой работы, поэтому затруднений не должно возникнуть. (выборочная проверка синквейнов).
— Большое спасибо вам за урок. Все потрудись хорошо. До свидания, ребята!
Анализ. На данном уроке нами использовались средства наглядности (презентация, опорные схемы геометрических фигур), работа в парах, фронтальная работа, применялся исследовательский подход при решении арифметической задачи, технология критического мышления.
Использование наглядности на уроках открытия нового знания способствует тому, что у школьников, благодаря зрительному восприятию геометрических фигур, формируются представления, правильно отображающие объективную действительность, и вместе с тем воспринимаемые явления анализируются и обобщаются в связи с учебными задачами.
Также нами использовался метод наглядности при проверке знаний учащихся (зрительная опора), мы предложили им картинки с изображением геометрических фигур для самостоятельной работы.
Средства наглядности на данном уроке стимулировали познавательный интерес к изучаемой теме, способствовали развитию эмоционального отношения к обучению.
Работа в парах на данном уроке предполагает активное включение каждого ученика в процесс усвоения учебного материала, самостоятельность, инициативность, формирует развитие социальных навыков в процессе групповых взаимодействий.
Задания, выполняемые детьми в паре, рассчитано на то, что обучающиеся выполняют индивидуально, а затем осуществляют взаимоконтроль. Эта часть работы заключается в нахождении заданных фигур, с классификацией фигур по разным признакам (по цвету, фигуры, имеющие углы и не имеющие углов, плоские и объемные тела). Задание предполагает развитие у школьников «геометрического зрения», логических УУД — анализ, сравнение.
Фронтальная работа предполагала решение с классом задач из учебника, обсуждение нового материала, работу над ошибками. Фронтальная работа способствовала включению школьников в работу класса, помогла выявить знания учеников и определить наиболее слабые места в их знаниях, внести уточнения. С помощью этой формы работы были включены в общую деятельность те школьники, которые по тем или иным причинам отключились от общей работы класса.
Исследовательский метод обучения на данном уроке применялся в ходе решения арифметической задачи. Этот метод, предусматривал организацию поисковой, познавательной деятельности учащихся путём постановки познавательной и практической задач, требующих самостоятельного творческого решения. В ходе решения арифметической задачи сначала выдвигались предположения (гипотезы) о возможных числовых значениях искомых, они проверялись с помощью вычислений и рассуждений, затем полученные результаты анализировались и выдвигались новые предположения с учетом полученных результатов.
Использование на данном уроке приема синквейн ТРКМ способствовал развитию личностных качеств учащихся, умения анализировать и синтезировать информацию по пройденному на уроке материалу, а также некоторой эмоциональной разгрузке школьников.
В качестве способов оценивания деятельности школьников использовалась словесная оценка, поощрения, «Умница!», «Молодец!», «Отлично!», если есть маленькие недочёты — «Хорошо», «Мне нравится, как ты стараешься», «Отлично!», «Хорошо, спасибо, тебя было интересно слушать», «Не огорчайся, у тебя все получится, только давай делать так,…», «Смотри, оказывается, можешь! Ведь получилось же, молодец!». На уроке использовался прием самооценки школьников «синквейн», а также мы заполняли «листы достижений», в которых фиксировали текущие оценки по всем формируемым на данном уроке навыкам.







