Рассмотрено введение демпфирования в автономные инерциальные системы, обеспечивающее уменьшение нежелательных колебаний. Оценены методы введения демпфирования в автономные инерциальные системы. При моделировании автономной инерциальной системы с обратной связью определены дополнительные погрешности в показаний скорости и координат, и также оценена эффективность использования такого метода введения демпфирования.
Ключевые слова: инерциальная система, автономная, демпфирование, погрешность, возмущение, акселерометр, гироскоп.
Инерциальные системы имеют в своём составе датчики линейного ускорения (акселерометры) и угловой скорости (гироскопы или пары акселерометров, измеряющих центробежное ускорение). С их помощью можно определить отклонение связанной с корпусом прибора системы координат от системы ориентации, связанной с Землёй, получив углы: рыскание (курс), тангаж и крен. В инерциальной системе обработаны первичные информации, снимаемые с акселерометров и гироскопов, затем преобразованы сигналы, удобные для решения ряда различных задач управления. При этом, данная система, основанная на свойствах инерции тел, являющаяся автономной, т. е. не требующей наличия внешних ориентиров или поступающих из вне сигналов [1].
Широкое применение автономных инерциальных систем в устройствах навигации и управления (летательными аппаратами, судов, поездом и пр.) обусловлено рядом присущих им достоинств технического и оперативно-тактического характера, к числу которых относятся: независимость работы от окружающей среды и внешних источников информации; скрытность работы ввиду отсутствия каких-либо излучений; высокая помехозащищённость от средств воздействия противника; высокая надёжность, значительный ресурс непрерывной работы в режиме боевого дежурства [2]. К недостаткам таких систем относятся дополнительные погрешности от нежелательных колебаний (возмущение), нелинейности и непостоянства показаний акселерометров и гироскопов, также наличие накапливания погрешностей с течением времени.
Введение демпфирования невозмущаемых колебаний инерциальных систем
В рамках этой статьи рассмотрена инерциальная система, состоящая из гироскопа вертикали, акселерометра и вычислительных устройств (первичного и вторичного интеграторов), которые обеспечивают измерить и подать соответствующую информацию об ее скоростях и координатах в систему навигации и управления (рис. 1) [3].
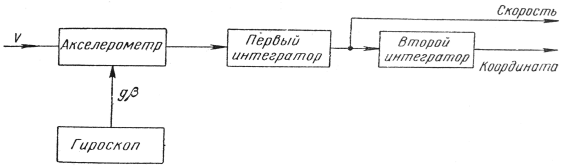
Рис. 1
Инструментальные ошибки такой инерциальной системы, так же как и не точности начальной установки гироскопа и акселерометра, вызывают незатухающие колебания с периодом невозмущаемости или близким к нему. Эти колебания создают от начальных нежелательные смещения по трём осям ориентации платформы инерциальной системы, что увеличивают погрешности показаний скорости и координат. Колебания возникают и в том случае, когда в начальный момент времени платформа системы была вертикальна (горизонтальна), т. е. совпадала с направлением силовых линий гравитационного поля и угловая скорость ее относительно Земли равнялась горизонтальной составляющей угловой скорости вращения Земли, так как платформа инерциальной системы остаётся в начальный момент при отсутствии коррекции «внешней» информации [4].
Из проведённого анализа следует, что применение такой схемы, в которой учёт вращения Земли, т. е. периферической скорости, производится вычитанием ее из показаний первого интегратора, возможно только при условии, что колебания платформы инерциальной системы будут погашены, т. е. в систему будет введено демпфирование. Методов введения демпфирования может быть предложено много. По-видимому, наиболее простым следует признать метод, который заключается в следующем. На гироскоп вертикали помимо момента, пропорционального интегралу от ускорений, накладывается дополнительный момент, пропорциональный самому ускорению. Следует, что добавление момента, пропорционального измеренному ускорению, создаёт демпфирование колебаний гировертикали. Однако, кроме демпфирования, этот момент создаст ещё и возмущение. Особенностью этого возмущения является то, что оно зависит от второй производной скорости по времени, т. е. от скорости изменения величины ускорения. Следовательно, будет имеет скачкообразное изменение ускорением [5–6].
Возможны и другие методы введения демпфирования в инерциальные системы. В частности, охват первого интегратора обратной связью также приведёт к появлению затухания в системе (рис. 2).
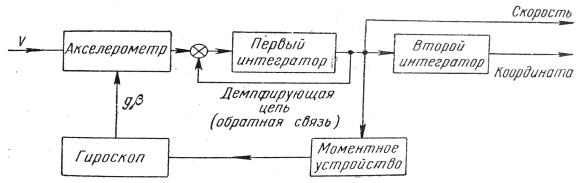
Рис. 2
В этом случае на первый интегратор будет поступать сигнал не только от акселерометра, но и от самого интегратора. Если значение, выдаваемое интегратором, обозначить через x, то уравнение движения гироскопа вертикали в данном случае может быть представлено в следующем виде:
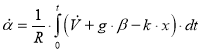 , (1)
, (1)
где α — угол отклонения оси гироскопа от вертикального направления, β — относительный угол поворота, t — время движения, φ = α + β — угол поворота вертикали, g — величина гравитационного ускорения, V — линейная скорость движения инерциальной системы, R — величина радиуса Земли (при пренебрежении высотой оси инерциальной системы над поверхностью Земли), k — коэффициент пропорциональности.
В тоже время в соответствии с выбранной схемой
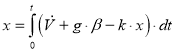 . (2)
. (2)
Сравнивая оба уравнения, найдём, что
![]() , (3)
, (3)
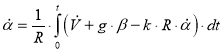 . (4)
. (4)
С учётом условия α·=V/R–β· получено следующее дифференциальное уравнение:
![]() . (5)
. (5)
Левая часть этого уравнения характеризует введение демпфирования в инерциальную систему, а правая — возмущения системы. Рассмотрим в качестве примера погрешности такой схемы моделирования при полуапериодическом затухании. В этом случае решение уравнения (5) будет иметь вид:
![]() , (6)
, (6)
где A — амплитуда колебания (A=2V·/g), δ — фаза колебания, а p — частота колебания (p=√(g/2R)). При этом за половину периода (T/2 = π/p) амплитуда уменьшится примерно в двадцать три раза, следовательно в течение половины периода погрешность станет меньше пяти процентов от начальной амплитуды колебаний данной системы, т. е. рассмотренная система демпфирована. Таким образом, введение демпфирования обеспечивает возможность устранения невозмущаемых колебаний инерциальных систем и уменьшения дополнительных погрешностей.
Дополнительные погрешности впоказаний скорости икоординат инерциальных систем свведением демпфирования
Ошибки автономной инерциальной системы в определении пройдённого пути представляют собой «расходящиеся» колебания с периодом Шулера. При охвате первого интегратора обратной связью возмущения в инерциальной системе создаются самой скоростью движения. Таким образом, при движении с постоянным ускорением всегда имеется возмущение, возникающее в процессе появления ускорения и вызывающее нежелательные колебания инерциальной системы [7–8]. Таким образом, даже при движении без ускорений положение равновесия в такой системе будет отклонено от вертикали на угол kV/g. Если положить k таким, чтобы затухание было полуапериодическим, т. е. чтобы
![]() , (7)
, (7)
то максимальный угол отклонения положения равновесия от вертикального направления при движении без ускорений будет равен
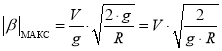 . (8)
. (8)
Выше рассматривались только погрешности положения гировертикали, т. е. значение угла β, но не определялись погрешности показаний инерциальной системы. Очевидно, что демпфирование вносит существенные погрешности в показания скорости и координат. Погрешности скорости и координат могут быть найдены как результат одного и двойного интегрирования величины g·β. Рассмотрим в качестве примера погрешности данной схемы моделирования при полуапериодическом затухании. Если полагать, что (V’=0), то погрешность показания скорости может быть выражаться формулой:
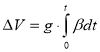 . (9)
. (9)
Используя уравнение (6) и соотношение амплитуды колебания A=2V*/g с условием начальной фазы колебания δ = 0, получим:
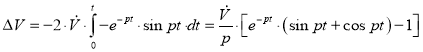 . (10)
. (10)
Следовательно, погрешность показания координат определяется уравнением:
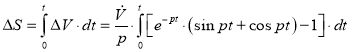 , (11)
, (11)
Значит:
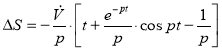 , (12)
, (12)
т. е. состоит из части, непрерывно возрастающей (до тех пор, пока система движется с ускорением), затухающей колебательной части и постоянной составляющей. Видно, что демпфирование, вводимое в инерциальную систему, кроме затухания колебаний вносит и погрешности как в положение гировертикали, так и в показания скорости и координат [9]. Погрешности эти значительны, и естественно, что необходимо учитывать при исследовании и разработки данной системы.
Выводы
Обсуждено введение демпфирования в автономные инерциальные системы, обеспечивающего уменьшение нежелательных колебаний. Оценены методы введения демпфирования в автономные инерциальные системы. При моделировании основной схемы с использованием обратной связи охватом первого интегратора определены формулы дополнительных погрешностей в показаний скорости и координат.
Показано, что автономное демпфирование не может полностью устранить нежелательные колебания и погрешности в данной системе. Уменьшение этих погрешностей, вызываемых демпфированием, можно осуществить за счёт так называемой внешней информации, т. е. за счёт внесения коррекции в демпфирующий сигнал от источников информации (от систем GPS, ГЛОНАСС, Galileo, систем навигации по геофизическим полям, систем навигации по картам местности и др.), не связанных с самой инерциальной системой. Однако такого рода коррекции, хотя и уменьшает погрешности, вносимые в показания демпфированием системы, но, к сожалению, делает инерциальную систему не полностью автономной. Поэтому, оптимальным решением оказывается какой метод, зависящий от технических требований исследования и разработки конкретных инерциальных систем.
Литература:
- Пешехонов В. Г. Ключевые задачи современной автономной навигации // Гироскопия и навигация. 1996. № 1(12). С.48–55.
- Зельдович С. М., и др. Автокомпенсация инструментальных погрешностей гиросистем. -Ленинград: Судостроение, 1976. -255 с.
- M. S. Grewal, L. R. Weill, A. P. Andrews. Global positioning systems, inertial-navigation, and integration. New Jersey: John Wiley & Sons, 2nd ed., 2007.
- Fraden J. Handbook of modern sensors: Physics designs and applications. NewYork: Springer-Verlag, 2010. 579 p.
- Pham Anh Tuan, et al. Methods of expanding the measurement range of micro-opto-electro-mechanical angular velocity transducer // Measurement techniques, Vol. 60, No. 6, September, 2017.
- G. F. Franklin, J. D. Powell, A. Emami-Naeini. Feedback control of dynamic systems. Menlo Park, CA: Addison Wesley, 4th ed., 2002.
- Бидерман В. Л. Прикладная теория механических колебаний. М.: Высшая школа, 1972. 416 с.
- Боднер В. А. и др. К теории инерциальных демпфированных систем с произвольным периодом, инвариантных по отношению к маневрированию объекта // Известия АН СССР, ОТН, Энергетика и автоматика, № 3, 1959.
- Андреев В. Д. Теория инерциальной навигации: автономные системы. — М.: Наука, 1966.

