Целью было написать программу, определяющую местоположения тел, движущихся по инерции (баллистически) в космосе. Телами могут быть планеты, их естественные или искусственные спутники, Солнце, а также другие звезды со своими планетными системами. Программа предназначена для проведений численных экспериментов по запуску искусственных тел по тем или иным траекториям, или наблюдения поведений планетарных систем.
Программа реализуется в двумерном варианте, который позволяет увидеть основные закономерности, потому что планетарные системы близки к плоским.
Моделирование движения произвольного количества тел в космосе — Земли, Луны и спутников/ракет в 2d пространстве происходит следующим образом: пусть имеется N объектов (космических тел), у каждого объекта есть следующие характеристики: текущее положение — x, y; текущая скорость — vX, vY; текущее ускорение — aX, aY; масса — m; сила, действующая на тело — xF, yF; следующие координаты положения — yNext, xNext (для метода Гюна); следующая скорость — yVNext, xVNext; радиус для отрисовки — R; радиус физический — physR. В программе мы объект реализуем в виде класса, а всё множество объектов в виде массива экземпляров класса. Имеется массив OfS (object of space) из N объектов. Объекты с номерами i и j притягиваются силой:
![]() =
= 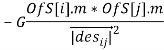 *
* ![]() , где G — гравитационная постоянная, а
, где G — гравитационная постоянная, а ![]() — вектор, направленный от положения тела i к положению тела j. Суммарную силу, воздействующую на тело i, мы получаем, как сумму всех сил между телами, за исключением отношения тела к самому себе. Перемещение тел мы вычисляем либо по схеме Эйлера, либо по методу Гюна [http://www.physchem.chimfak.rsu.ru/Source/NumMethods/ODE.html]. Для этого мы физическое время разбиваем на небольшие шаги (в нашей программе для системы Земля-Луна это около 1 секунды). В бесконечном цикле физическое время увеличивается на заданный шаг. В каждый текущий момент времени мы вычисляем суммарную силу, действующую на каждое тело, способом, описанным выше, включая компоненты по x и y. Затем по второму закону Ньютона вычисляем ускорение для каждого тела. Учитывая предыдущие значения скорости, вычисляем приближенную скорость в текущий момент, а также приближенно вычисляем следующее текущее положение тела. Для метода Эйлера этого достаточно, для метода Гюна мы в качестве следующих значений скорости и положения, вычисляем усредненные значения между текущим значением и следующим. Как для метода Эйлера, так и для метода Гюна нужно задавать начальные положения и скорости тел. В качестве системы координат используем систему, в которой началом является центр масс Земли и Луны. Начальные координаты «y» для Земли и Луны присваиваем нулю. Начальные значения x для Земли и Луны вычисляем таким образом, чтобы произведение массы Земли на |x| Земли равнялось масса Луны*|x|Луны, а расстояние между ними равнялось 450 млн. метров. Начальная скорость Луны по x равна 0, по y равна 1000 м/с, начальная скорость Земли по x равна 0, по y равна -12,6 м/с. Это примерно соответствует реальным астрономическим значениям. Одна из задач проекта — моделирование движений спутников/ракет. Нам удобно задавать начальные движения спутников/ракет, считая их расположенными на круговой орбите вокруг Земли, и начинающих движение с некоторой заданной скоростью. Для экспериментов нам удобно задавать высоту орбиты; значение сектора в градусах, под которым стартует спутник/ракета; начальная скорость спутника/ракеты. Значения задаются в системе координат, которая неподвижна относительно Земли, с началом координат в центре Земли. Сначала вычислим координаты и скорость спутника/ракеты, в системе координат Земли, далее, зная положение и скорость Земли в общей системе координат, получим начальные координаты и скорость спутника/ракеты в общей системе координат.
— вектор, направленный от положения тела i к положению тела j. Суммарную силу, воздействующую на тело i, мы получаем, как сумму всех сил между телами, за исключением отношения тела к самому себе. Перемещение тел мы вычисляем либо по схеме Эйлера, либо по методу Гюна [http://www.physchem.chimfak.rsu.ru/Source/NumMethods/ODE.html]. Для этого мы физическое время разбиваем на небольшие шаги (в нашей программе для системы Земля-Луна это около 1 секунды). В бесконечном цикле физическое время увеличивается на заданный шаг. В каждый текущий момент времени мы вычисляем суммарную силу, действующую на каждое тело, способом, описанным выше, включая компоненты по x и y. Затем по второму закону Ньютона вычисляем ускорение для каждого тела. Учитывая предыдущие значения скорости, вычисляем приближенную скорость в текущий момент, а также приближенно вычисляем следующее текущее положение тела. Для метода Эйлера этого достаточно, для метода Гюна мы в качестве следующих значений скорости и положения, вычисляем усредненные значения между текущим значением и следующим. Как для метода Эйлера, так и для метода Гюна нужно задавать начальные положения и скорости тел. В качестве системы координат используем систему, в которой началом является центр масс Земли и Луны. Начальные координаты «y» для Земли и Луны присваиваем нулю. Начальные значения x для Земли и Луны вычисляем таким образом, чтобы произведение массы Земли на |x| Земли равнялось масса Луны*|x|Луны, а расстояние между ними равнялось 450 млн. метров. Начальная скорость Луны по x равна 0, по y равна 1000 м/с, начальная скорость Земли по x равна 0, по y равна -12,6 м/с. Это примерно соответствует реальным астрономическим значениям. Одна из задач проекта — моделирование движений спутников/ракет. Нам удобно задавать начальные движения спутников/ракет, считая их расположенными на круговой орбите вокруг Земли, и начинающих движение с некоторой заданной скоростью. Для экспериментов нам удобно задавать высоту орбиты; значение сектора в градусах, под которым стартует спутник/ракета; начальная скорость спутника/ракеты. Значения задаются в системе координат, которая неподвижна относительно Земли, с началом координат в центре Земли. Сначала вычислим координаты и скорость спутника/ракеты, в системе координат Земли, далее, зная положение и скорость Земли в общей системе координат, получим начальные координаты и скорость спутника/ракеты в общей системе координат.
Пусть Xx, Yy — координаты спутника/ракеты в системе координат Земли, vVx, vVy — компоненты скорости спутника/ракеты в системе координат Земли. Тогда Хх = (R+h)*cos(alpha), Yy = (R+h)*sin(alpha). vVx = v*cos(alpha+pi/2), vVy = v*sin(alpha+pi/2). Пусть xE, yE — координаты Земли в общей системе координат, vXe, vYe — скорость Земли в общей системе координат. Тогда начальные значения положения и скорости спутника/ракеты в общей системе координат равны: X = xE+Xx; Y = yE+Yy; vX = vXe+vVx; vY = vYe+vVy.
В программе различаются: физическое время, реальное время. Реальное время — это время, которое отсчитывается встроенными часами, в которых живёт пользователь. Физическое время — это время эксперимента, которое, как правило, движется во много раз быстрее реального времени. Для наблюдения за ходом эксперимента, мы выводим в графическое окно условное обозначение Земли, Луны и прочих объектов, текущее время в сутках. Для наглядности реализуем след от каждого движущегося тела. В окно отображаем очередные начисленные положения тел с частотой около 50 раз в секунду. Между двумя отображениями обычно проходит несколько сотен или тысяч шагов физического времени. Соотношения расчета процесса, визуализации, физического и реального времени показаны на рисунке 1.
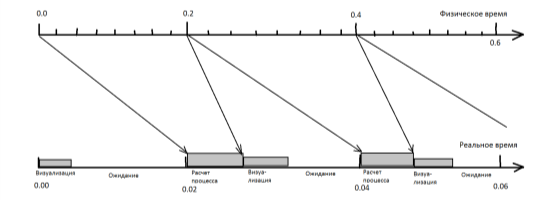
Рис. 1
Графическое отображение основывается на простой либо OpenGL графике. Учитывая сложность 3д графики, на основе простой графики будет реализовываться 2д вариант. После освоения OpenGL будет реализован 3д вариант. Все объекты будут воспроизводиться в виде кружочков или шаров различного диаметра. Интервал воспроизведения dt (время между перерисовками) и значение дельта t будут задавать масштаб воспроизведения по времени. Например, при dt = 0,01 с. = 1000 микросекунд и дельта t = 100 с. масштаб будет равен 100/0,01–10000. То есть, процесс на экране будет продвигаться примерно в 10000 раз быстрее реальных процессов: например, Луна сделает оборот вокруг Земли не за 29 дней, а за 250 секунд или примерно за 4 минуты. Масштаб можно будет регулировать. Каждый эксперимент будет начинаться с ввода начальных координат и скоростей Земли, Лун и спутника. Например: E.x = 0; M.x = 400 000 000 метра; S.x0 =300000; E.y=0; M.y = 0; S.y0 = 0; E.Vx0 = 0; M.Vx0 = 0; S.Vx0 = 800; E.Vy0 = 0; M.Vy0 = 1000 км/с; S.Vy0 = 300. В окончательной реализации для варианта Земля-Луна, для нас удобен был вариант, когда исходными данными являются высота опорной орбиты(то есть круговой орбиты вокруг Земли на высотах 200–500 км.), скорость старта с орбиты(в системе относительно Земли) и некоторый угол(сектор), который составляет радиус-вектор от центра Земли к спутнику и направлением оси x в момент старта. Для вычисления стартовых значениях в универсальной системе (с началом координат в центре масс Земля-Луна) мы используем формулы векторной алгебры, тригонометрии и пересчет координат из системы «Земля» в универсальную систему.
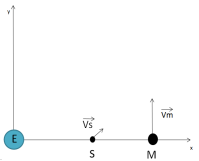
Рис. 2
Проведены вычислительные эксперименты для системы Земля-Луна. Первый эксперимент — попадание спутника с некоторой опорной орбиты в Луну. Подбором получили следующие начальные значения: высота орбиты — 300000 м (300 км), угол сектора — 231.5 градусов, начальная скорость — 10850 м/с, время подлёта к Луне — 3 дня. Ход эксперимента изображен на рисунках 3, 4.
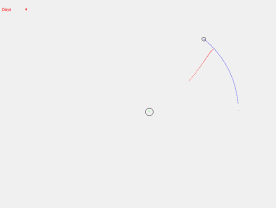
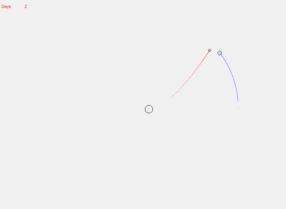
Рис. 3 Рис. 4
Второй эксперимент -Облёт спутником Луны и возвращение к Земле: скорость — 10850 м/с, время подлёта к Луне — 3 дня, высота орбиты — 300000 м (300 км), угол сектора — 235 градусов, начальная скорость — 10850 м/с, время подлёта к Луне — 3 дня.
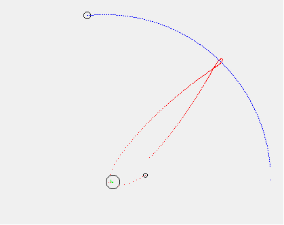
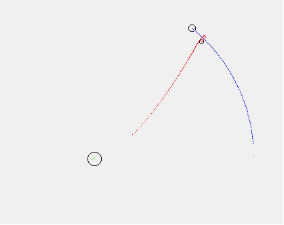
Рис. 5 Рис. 6
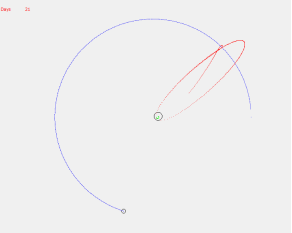
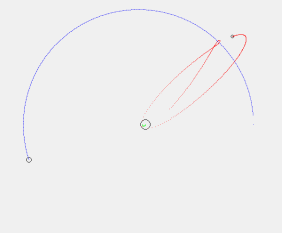
Рис. 7 Рис. 8
Гравитационный манёвр, при котором спутник получает дополнительный импульс от Луны и покидает гравитационное поле Земли: высота орбиты — 300000 м (300 км), угол сектора — 229 градусов, начальная скорость — 10850 м/с, время подлёта к Луне — 3 дня.
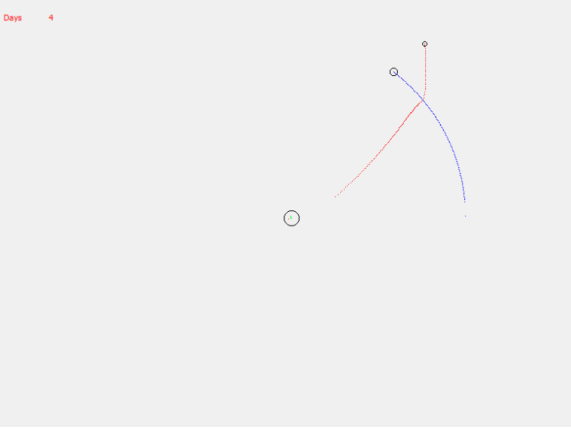
Рис. 9
Описание экспериментов для двойной звёздной системы «Сириус»
Известно, что одна из самых близких к Солнцу звезд — Сириус на самом деле представляет систему из 2-х звезд: Сириус A и Сириус B. В фантастических рассказах часто пишут о планетах, для которых светят два Солнца. Исследуем, насколько это реально.
Сначала подберем параметры для 2-х небесных тел, схожих с Сириус A и Сириус B. Мы подобрали параметры, чтобы движение наших компьютерных моделей звёзд было схожим с реальными. Заметим, что максимальное расстояние между Сириус A и Сириус B составляет около 37 астрономических единиц (а.е. — среднее расстояние от Земли до Солнца). В качестве экспериментальных планет запускаем компьютерные модели планет, с массой, близкой к земной массе (в качестве небесных тел в массиве OfS с номерами 2, 3… и т. д.). Запуск с непосредственной близости к звёздам (2–3 а.е.) очень быстро приводит к тому, что гравитационные воздействия звёзд обеспечивают гравитационное ускорение планет и выброс их из гравитационного поля Сириуса. Надежду на устойчивые орбиты составляют движения планет, расстояния которых до Сириус A и Сириус B достаточно велико (20 и более а. е.). Для этого программным образом создадим 10 планет, которые запускаем на круговых орбитах вокруг центра масс Сириус A и Сириус B, начиная с расстояния 30 а.е. с увеличением радиуса орбит на 6 а.е. Таким образом, самая дальняя планета находится на расстоянии 90 а.е. от центра масс. Для сравнения, самая дальняя планета Солнечной системы находится на расстоянии около 30 а.е. от Солнца. Планеты запускаем, приблизительно равномерно распределив их угловые значения движения вокруг начала координат. Скорость планеты с орбитой радиуса R мы вычисляем исходя из того, что сила притяжения суммарной массы Сириуса A и Сириуса B должно быть равно центростремительной силе. То есть, по формуле V = ![]() , где M — сумма масс Сириуса A и Сириуса B, G — гравитационная постоянная.
, где M — сумма масс Сириуса A и Сириуса B, G — гравитационная постоянная.
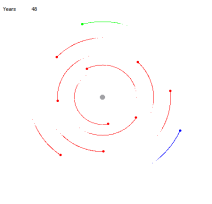
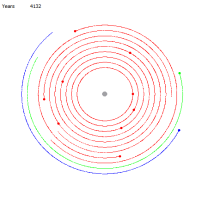
Рис. 10 Рис. 11
Для начала покажем, что это обычные круговые орбиты. Для этого в центр масс поместим условную звезду, с массой равной сумме масс Сириуса A и Сириуса B. На рисунках 10, 11 соответственно показано расстояние, близкое к началу движения и через 4000 лет. Мы видим, что орбиты устойчивы — остаются круговыми. Теперь точно так же запустим планеты, оставив в центре планетарной две звезды: Сириус A и Сириус B. На рисунках 12, 13, 14, 15 соответственно показано состояние планетарной системы в начале движения, через 255 лет, 590 лет и 4000 лет.
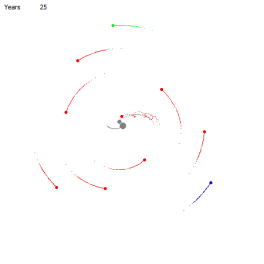
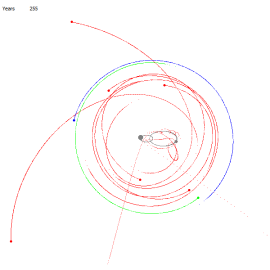
Рис. 12 Рис. 13
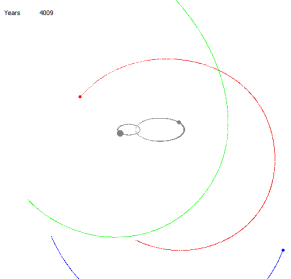
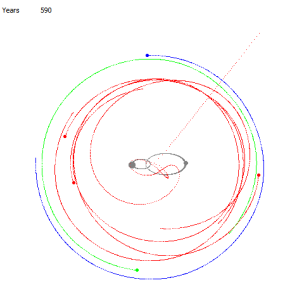
Рис. 14 Рис. 15
Эксперимент показывает, что воздействие двух движущихся вокруг общего центра масс звёзд, приводит к неустойчивости планетарных орбит, даже расположенных достаточно далеко (по Солнечным меркам) от центра масс Сириус A и Сириус B. Поэтому, фантастические рассказы о планетарных системах с 2-мя светилами не реалистичны.
Разработанная программа с небольшими доработками позволяет провести много интересных экспериментов, в частности для Солнечной системы. Например,
1) Траектория полётов от Земли к Марсу или Венере;
2) Необходимая стартовая скорость с орбиты Земли для покидания гравитационного поля Солнца с использованием гравитационного манёвра у Юпитера. Заметим, что аппараты Вояджер — 1 и Вояджер — 2 стартовали со скоростью около 15 км/с, и в конечном счёте покинули гравитационное поле Солнца, хотя третья космическая скорость равна 16 км/с. Дополнительную энергию Вояджеры получили при гравитационном манёвре около Юпитера.
3) Необходимая скорость с орбиты Земли для достижения Солнца (теоретически 30 км/с).
4) Необходимая скорость с орбиты Земли для достижения Солнца с использованием гравитационного манёвра вокруг Юпитера (предположительно около 13 км/с).
Модификация вычислительной части для 3d пространства достаточно проста, координата z вычисляется аналогично координатам x и y. Но отображение 3d варианта требует привлечения более развитых средств (OpenGL или DirectX).
Для моделирования взаимодействия на больших расстояниях имеет смысл учесть скорость гравитационного воздействия, равной скорости света. Для этого каждое тело должно хранить некоторый архив своих местоположений. Метод Гюна позволяет легко включить не только баллистические траектории, но и движения ракет с учетом мощностей двигателей и переменной массы ракеты.
Литература:
- Ивашкин В. В. ИПМ им. М. В. Келдыша, РАН Москва, 2001. Об оптимальных траекториях полета к Луне в системе Земля-Луна-Солнце. URL: http://www.keldysh.ru/papers/2001/prep85/prep2001_85.html
- Кафедра физхимии ЮФУ (РГУ) Численные методы и программирование Материалы к лекционному курсу Лектор — ст. преп. Щербаков И. Н. «Решение обыкновенных дифференциальных уравнений» URL: http://www.physchem.chimfak.rsu.ru/Source/NumMethods/ODE.html
- Программа «Celestia» URL: https://celestia.space/
- URL: http://doc.crossplatform.ru/qt/4.7.x/qwidget.html







