Stochastic Riemannian Optimization techniques application for Gaussian Mixture Models



In this paper I describe my approach towards solving Gaussian Mixture Models (GMM) problem. I am using to the rich Riemannian geometry of positive definite matrices, using which I can cast Gaussian Mixture Models parameter estimation as a Riemannian optimization problem. I develop Riemannian batch and stochastic gradient algorithms.

1. Introduction

Gaussian Mixture Model (GMM) is given by:

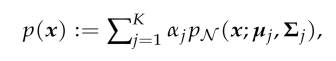
where:

the following is the Gaussian (with mentioned below parameters)

Vector:

Mean:

Covarience:

2. Methods for Riemannian optimization

Methods for manifold optimization operate iteratively by following algorithm:

‒ First, obtain a descent direction, and which is to find a vector in tangent space which minimize the cost function if we move along it;

‒ Then, perform a line-search along a smooth curve on the manifold to obtain sufficient minimization and assure convergence.

Such a smooth curve which is parametrized by a point on the manifold and a direction is called retraction. A retraction is a smooth mapping Ret from the tangent bundle TM to the manifold M. The restriction of retraction to T_X, Ret_X: T_X → M, is a smooth mapping with:

1. Ret_X(0) = x, where 0 denotes the zero element of T_X.
2. D Ret_X(0) = idT_X, where D Ret_X denotes the derivative of Ret_X and id T_X denotes the identity mapping on T_X.

The candidate for retraction on Riemannian manifolds is the exponential map. The exponential map Exp_X: T_X → M is defined as Exp_X v = γ(1), where γ is the geodesic satisfying the conditions γ(0) = x and γ˙(0) = v. These methods are based on gradients.

The gradient on a Riemannian manifold is defined as the vector ∇ f(x) in tangent space such that D f(x)ξ = h∇ f(x), ξi, for ξ ∈ T_X, where <·, ·> is the inner product in the tangent space T_X.

3. Riemannian stochastic optimization algorithm

Here we consider the stochastic gradient descent (Stochastic Gradient Descent algorithm) algorithm (3.1 formula):

where Ret_X is a suitable retraction (to be specialized later). I assume for my analysis of (3.1) the following fairly standard conditions:

(i) 3.1 function satisfies the Lipschitz growth bound

(ii)
The stochastic gradients in all iterations are unbiased, that is:

(iii)
The stochastic gradients have bounded variance, so that

When the retraction is the exponential map, condition (i) can be reexpressed as (provided that Exp−1 y (·) exists)

4. Stochastic Gradient Descent algorithm application for Gaussian Mixture Models

Here I investigate if Stochastic Gradient Descent algorithm based on retractions satisfies the conditions needed for obtaining a global rate of convergence when applied to my Gaussian Mixture Models optimization problems.

Since Euclidean retraction turns out to be computationally more effective than many other retractions, I perform the analysis below for Euclidean retraction. Recall that I are maximizing a cost of the form:

using Stochastic Gradient Descent algorithm. In a concrete realization, each function f_i is set to the penalized log-likelihood for a batch of observations (a data points). To put things in simpler notation, assume that each f_i corresponds to a single observation. Thus

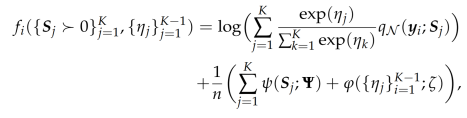
Since I am maximizing, the update formula for Stochastic Gradient Descent algorithm is

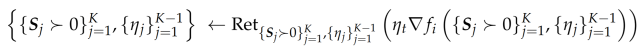
where i is a randomly chosen index between 1 and n. Note that, the conditions needed for a global rate of convergence are not satisfied on the entire set of positive definite matrices. In particular, to apply my convergence results for Stochastic Gradient Descent algorithm I need to show that the iterates stay within a compact set.

5. Conclusions and future work

In this paper, I proposed a reformulation for the Gaussian Mixture Models problem that can make Riemannian manifold optimization. Furthermore, I developed a global convergence theory for Stochastic Gradient Descent algorithm. I applied this theory to the Gaussian Mixture Models modeling.

References:

1. R. W. Keener. Theoretical Statistics. Springer Texts in Statistics. Springer, 2010.
2. John M. Lee. Introduction to Smooth Manifolds. Springer, 2012.
3. G. J. McLachlan and D. Peel. Finite mixture models. John Wiley and Sons, 2000.
4. Ankur Moitra and Gregory Valiant. Settling the polynomial learnability of mixtures of Gaussians. In 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS), pages 93–102, 2010.
5. Kevin P. Murphy. Machine Learning: A Probabilistic Perspective. MIT Press, 2012.
6. Jorge Nocedal and Stephen J. Wright. Numerical Optimization. Springer, 2006.
7. Douglas A Reynolds, Thomas F Quatieri, and Robert B Dunn. Speaker verification using adapted Gaussian mixture models. Digital Signal Processing, 10(1–3):19–41, 2000.
8. Andrea Ridolfi, Jerome Idier, and Ali Mohammad-Djafari. Penalized maximum likelihood estimation for univariate normal mixture distributions. In Actes du 17e Colloque GRETSI, pages 259–262, 1999.
9. Wolfgang Ring and Benedikt Wirth. Optimization methods on Riemannian manifolds and their application to shape space. SIAM Journal on Optimization, 22(2):596–627, 2012.
10. Suvrit Sra and Reshad Hosseini. Geometric optimisation on positive definite matrices for elliptically contoured distributions. In Advances in Neural Information Processing Systems 26 (NIPS), pages 2562–2570, 2013.
11. Suvrit Sra and Reshad Hosseini. Conic geometric optimization on the manifold of positive definite matrices. SIAM Journal on Optimization, 25(1):713–739, 2015.
12. Constantin Udriste. Convex functions and optimization methods on Riemannian manifolds. Kluwer Academic, 1994.
13. Robert J Vanderbei and H Yurttan Benson. On formulating semidefinite programming problems as smooth convex nonlinear optimization problems. Technical Report ORFE-99–01, Department of Operations Research and Financial Engineering, Princeton University, Princeton NJ, 2000.
14. Bart Vandereycken. Low-rank matrix completion by Riemannian optimization. SIAM Journal on Optimization, 23(2):1214–1236, 2013.
    1. Wiesel. Geodesic convexity and covariance estimation. IEEE Transactions on Signal Processing, 60(12):6182–89, 2012.
15. Hongyi Zhang and Suvrit Sra. First-order methods for geodesically convex optimization. In 20 29th Annual Conference on Learning Theory (COLT), pages 1617–1638, 2016.
16. Hongyi Zhang, Sashank Reddi, and Suvrit Sra. Riemannian SVRG: Fast stochastic optimization on Riemannian manifolds. In Advances in Neural Information Processing Systems 29 (NIPS), pages 4592–4600, 2016.
17. P-A Absil, Robert Mahony, and Rodolphe Sepulchre. Optimization algorithms on matrix manifolds. Princeton University Press, 2009.
18. R. Bhatia. Positive Definite Matrices. Princeton University Press, 2007.
19. Srinadh Bhojanapalli, Anastasios Kyrillidis, and Sujay Sanghavi. Dropping convexity for faster semi-definite optimization. In 29th Annual Conference on Learning Theory (COLT), pages 530–582, 2016.
20. C. M. Bishop. Pattern recognition and machine learning. Springer, 2007.
21. Silvere Bonnabel. Stochastic gradient descent on Riemannian manifolds. IEEE Transactions on Automatic Control, 58(9):2217–2229, 2013.
22. Nicolas Boumal, Bamdev Mishra, P-A Absil, and Rodolphe Sepulchre. Manopt, a matlab toolbox for optimization on manifolds. The Journal of Machine Learning Research, 15(1):1455–1459, 2014.
23. Nicolas Boumal, P.-A Absil, and Coralia Cartis. Global rates of convergence for nonconvex optimization on manifolds. arXiv:1605.08101v1, 2016.