В работе рассматриваются использование алгоритма вЛСА для построения тематической модели коллекции текстов, написанных на естественном языке.
Ключевые слова: тематическое моделирование, векторная модель, вероятностный латентный семантический анализ, pLSA, вЛСА.
Данный алгоритм позволяет построить модель неявного (латентного) распределения документов коллекции и слов по темам, что позволит в результате найти тематическую схожесть документов, просто посчитав их расстояние в модели. Недостатком является необходимость в достаточном большом количестве обучающих документов, а также в необходимости пересчитывать модель каждый раз при добавлении нового документа.
Первым шагом работы данного алгоритма для каждого документа является составление векторной модели текста. Для этого строится матрица терм-документ отражающая количество вхождений каждого слова в каждый документ.
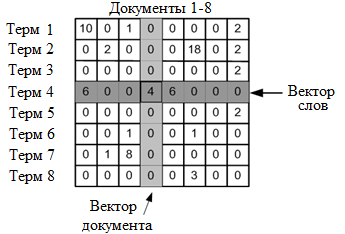
Для нахождения значения каждой ячейки данной матрицы, могут быть использованы различные данные, такие как количество вхождений каждого уникального слова в каждый из текстов, частота вхождения каждого уникального слова в каждый из анализируемых текстов, либо посчитанная метрика TF-IDF.
После произведения подобной операции над каждым из документов будет составлена общая матрица терм-документ.
В общем случае, алгоритм Вероятностного латентно-семантического анализа применяется для решения задачи тематического моделирования. Формальная постановка задачи такова:
Пусть 
— множество текстовых документов, 
— множество всех употребляемых в них терминов. Каждый документ 
представляет собой последовательность 
терминов 
из словаря , при этом термин может повторятся в документе множество раз.
Пусть существует конечное множество тем 
, и каждое употребление термина 
в каждом документе 
связано с некоторой темой 
, которая не известна. Формально тема определяется как дискретное вероятностное распределение в пространстве слов заданного словаря .
Введем дискретное пространство
. Тогда коллекция документов может быть рассмотрена как множество троек 
, выбранных случайным образом, независимо от дискретного распределения 
. Документы , термины являются наблюдаемыми переменными, а темы 
— скрытыми (латентными) переменными.
Для решения задачи требуется найти распределение терминов в темах 
для всех тем , и распределения тем в документах 
для всех документов d.
С учетом гипотезы условной независимости 
(распределения слов связаны с темами, а не с документами) по формуле полной вероятности можно получить вероятностную модель порождения документа :
В таком случае, вероятность возникновения пары «документ-слово» может быть выражена следующим образом:
Это уравнение данном случае является математическим представлением смешанной модели, показанной следующем рисунке. Данная модель показывает латентные связи документов со словами, проходящие через скрытый внутренний слой, который в данном случая отражает тему. На данном рисунке, элементы «d» отражают документы, элементы «z» — скрытый латентный параметр, в данном случае — темы, а элементы «w» — слова.
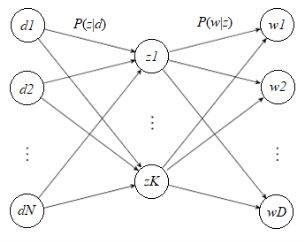
Для идентификации параметров тематической модели по коллекции документов применяется принцип максимизации правдоподобия, который приводит к задаче максимизации функционала:
Для решения данной задачи чаще всего используют EM-алгоритм (Expectation-Maximization, максимизация правдоподобия), состоящий из двух шагов.
На первом шаге, называемом «E-шаг», вычисляется значение условных вероятностей
для всех тем 
для каждого термина 
для всех документов 
. Для этого текущие значения параметров 
и 
выражают по формуле Байеса:
На втором шаге, называемом «M-шаг», решается обратная задача — по условным вероятностям тем 
вычисляются приближения и :
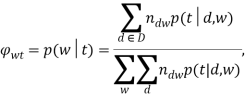
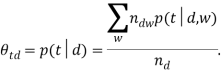
Описанный выше метод является основным представлением алгоритма вероятностного латентно-семантического анализа, получающего на вход частоты нахождения слов в документах, и выдающего распределения слов и документов по латентным темам.
Алгоритм pLSA в общем смысле является факторизацией матрицы условного распределения 
Итоговое матричное выражение выглядит так:
На следующем рисунке данные разложения отображены более наглядно.
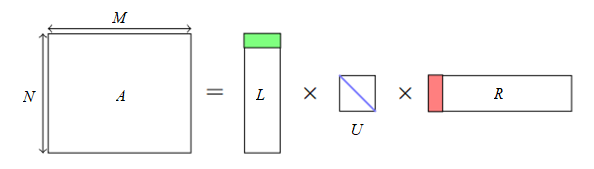
В отличие от матриц, получающихся в результате алгоритма обычного латентно-семантического анализа с использованием алгоритма SVD, данные матрицы всегда будут неотрицательными и нормализованными, и отражать определенные распределения вероятностей.
Полученные в результате матрицы отражают вероятности отношения документов и слов к определенным неявным тематикам, что служит опорой в алгоритме вычисления оценки схожести документов.
Литература:
- Gaussier E., Goutte C., Popat K., Chen F., A Hierarchical Model for Clustering and Categorizing Documents [Text] // In proceedings of the 24th BCS-IRSG European Colloquium on IR Research (ECIR-02). — Glasgow, 2002. — Pp. 229–247.
- Oneata D. Probabilistic Latent Semantic Analysis [Электронный ресурс]. URL: http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV1011/oneata.pdf
- Merce V. R.. Probabilistic Latent Semantic Analysis [Электронный ресурс]. URL: http://www.inf.ed.ac.uk/teaching/courses/tnlp/2016/Merce.pdf
