На кафедре «Прядение натуральных и химических волокон» УО «Витебский государственный технологический университет» разработана технология получения текстильного настенного покрытия. Основным процессом при производстве текстильных настенных покрытий является процесс термообработки. По результатам исследований установлено, что специфические свойства текстильных настенных покрытий во многом зависят от условий проведения процесса термообработки. Определено, что наиболее важными задачами при изучении термообработки текстильных настенных покрытий является определение зависимости между температурой среды, продолжительностью процесса термообработки и термическими свойствами материалов.
Текстильное настенное покрытие состоит из двух слоев, отличающихся друг от друга теплопроводностью и толщиной (рисунок 1), поэтому анализ процесса термообработки можно провести как анализ теплообмена в системе двух неограниченных пластин при нестационарных условиях.[1] Температуры наружных поверхностей покрытия равны tст1 tст2, причем tст1>tст2. Поэтому при установившимся процессе, количество тепла, подведенного к одной стороне покрытия и отведенного от другой стороны, равны между собой и не должны изменяться во времени, т.е. через каждый слой покрытия пройдет одно и то же количество тепла.
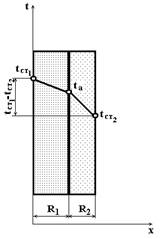
Рис. 1. Количество тепла, проходящее через слои настенного покрытия
Сформулируем постановку задачи процесса термообработки текстильных настенных покрытий в общем виде. Две неограниченные пластины толщиной R1 (флизелиновое или бумажное полотно) и R2 (текстильное полотно) с разными теплофизическими коэффициентами склеены между собой. Начальная температура их одинакова. В начальный момент времени поверхности мгновенно нагреваются до температуры Тс, которая поддерживается постоянной на протяжении всего процесса термообработки. Требуется найти распределение температуры по толщине системы из двух пластин.
Начало координат выберем в плоскости склеивания. Тогда краевые условия запишутся в следующем виде:
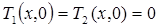 , (2)
, (2)
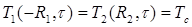 , (3)
, (3)
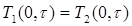 , (4)
, (4)
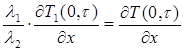 , (5)
, (5)
где l1 и l2 – коэффициенты теплопроводности флизелина (бумаги) и текстильного полотна соответственно (Вт/м*град).
Решения находим операционным методом преобразования Лапласа. Дифференциальные уравнения теплопроводности для одномерного потока тепла в двухслойной пластине имеют вид:
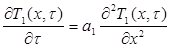 , (6)
, (6)
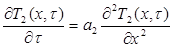 , (7)
, (7)
где а1 и а2 – коэффициенты температуропроводности флизелина (бумаги) и текстильного полотна соответственно (м2/с);
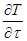 - температурное поле.
- температурное поле.
Применим преобразование Лапласа относительно переменной t. Получим обыкновенные дифференциальные уравнения второго порядка с постоянными коэффициентами относительно изображения:
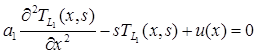 , (8)
, (8)
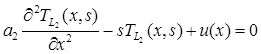 , (9)
, (9)
где u(x) – функция, описывающая начальное распределение температуры;
s – оператор Лапласа в интегральном преобразовании функции Т(х,t);
ТL(x,s) – изображение функции Т(х,t) в интегральном преобразовании Лапласа.
В данной работе рассматривался случай, когда в начальный момент времени температура во всех точках двухслойной пластины была одинакова и равна нулю. Согласно свойствам преобразования Лапласа, изображение производной можно записать по формуле:
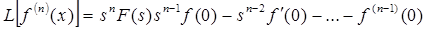 . (10)
. (10)
Отсюда полученные дифференциальные уравнения для изображений перепишем в следующем виде:
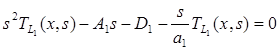 , (11)
, (11)
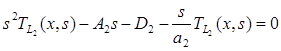 , (12)
, (12)
где A1, A2, D1, D2 – постоянные, определяемые из граничных условий.
Уравнения (11) и (12) являются простыми алгебраическими уравнениями относительно изображений. Решаем их, считая s простым числом:
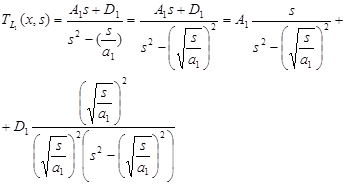 , (13)
, (13)
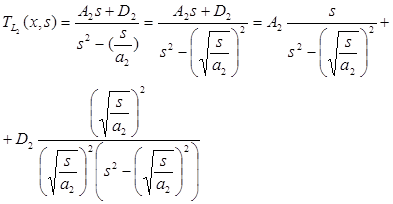 , (14)
, (14)
Согласно свойству линейности преобразования Лапласа:
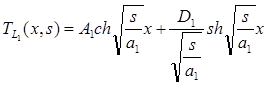 , (15)
, (15)
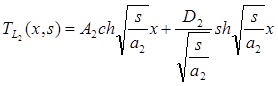 , (16)
, (16)
Заменим 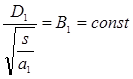 и
и 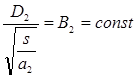
В итоге получим:
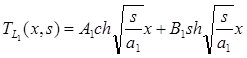 , (17)
, (17)
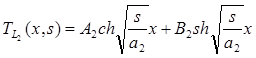 , (18)
, (18)
где А1, А2, В1, В2 – постоянные относительно х, зависящие от s величины и определяемые исходя из граничных условий.
Подставив граничные условия для изображений в уравнения (17) – (18), получим систему уравнений:
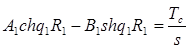 , (19)
, (19)
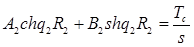 , (20)
, (20)
 где
где 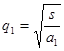 ;
; 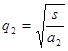 .
.
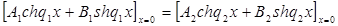 , (21а)
, (21а)
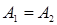 , (21)
, (21)
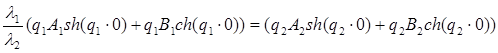 , (22а)
, (22а)
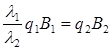 , (22)
, (22)
Решая систему из уравнений (19) – (22) относительно А1, А2, В1, В2, найдем корни, при подстановки которых в уравнения (17) – (18), получим решения дифференциальных уравнений для изображений.
Окончательно получим:
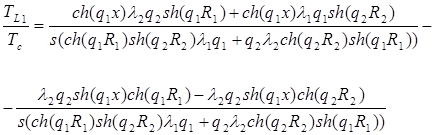 , (23)
, (23)
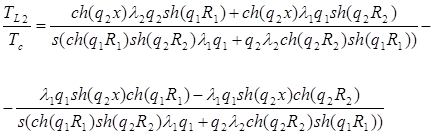 . (24)
. (24)
Из формул (23) и (24) можно получить формулу для изображения температуры клеевого слоя (x = 0) в заданный момент времен:
.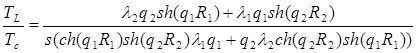 (25)
(25)
Приравнивая знаменатель соотношения (25) нулю, получим характеристическое уравнение:
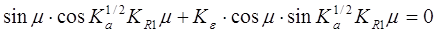 . (26)
. (26)
На основании соотношений (25) и (26) формулу для получения температуры клеевого слоя (Tц, x = 0) можно записать следующим образом:
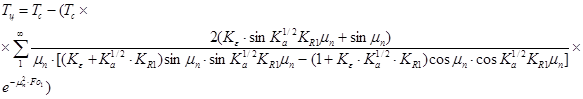 (27)
(27)
где 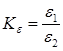 ,
, 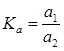 ,
, 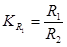 .
.
Полученная формула дает возможность точного определения температуры клеевого слоя в любой момент времени. Подстановка в полученную формулу значения температуры полимеризации клея, позволяет определить оптимальную продолжительность термообработки текстильных настенных покрытий.
Литература
- Лыков, А. В. Теория теплопроводности / А. В. Лыков. – Москва : Издательство «Высшая школа», 1967. – 600 с.

